ARSeasonalFit.GetTransformedTimeSeries Method

ARSeasonalFitGetTransformedTimeSeries Method

Returns the transformed series,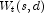

Namespace: Imsl.Stat
Assembly: ImslCS (in ImslCS.dll) Version: 6.5.2.0

Syntax

C++

Copy

public double[] GetTransformedTimeSeries()

Public Function GetTransformedTimeSeries As Double()

public:
array<double>^ GetTransformedTimeSeries()

member GetTransformedTimeSeries : unit -> float[]

Return Value

Type: Double
A double array of length z.Length or z.Length-NLost, depending upon the setting for the Exclude property.

Exceptions

Exception	Condition
MatrixSingularException	is thrown if the input matrix is singular.
TooManyCallsException	is thrown if the number of calls to the function has exceeded the maximum number of iterations times the number of moving average (MA) parameters + 1.
IncreaseErrRelException	is thrown if the bound for the relative error is too small.
NewInitialGuessException	is thrown if the iteration has not made good progress.
IllConditionedException	is thrown if the problem is ill-conditioned.
TooManyIterationsException	is thrown if the maximum number of iterations is exceeded.
TooManyFunctionEvaluationsException	is thrown if the maximum number of function evaluations is exceeded.
TooManyJacobianEvalException	is thrown if the maximum number of Jacobian evaluations is exceeded.
NonStationaryException	is thrown if the final maximum likelihood estimates for the time series are nonstationary.
SingularTriangularMatrixException	is thrown if the input triangular matrix is singular.

Remarks

is an array of length z.Length or z.Length-NLost containing the optimum seasonally adjusted, autoregressive series, where NLost is the first lost observations in this series that are dropped due to differencing. If the missing values are not dropped the first NLost values of will be set to Double.NaN. The NLost property can be used to obtain the number of lost observations.

The seasonal adjustment is done by selecting optimum values for $d_1,\ldots,d_m$ , $s_1,\ldots,s_m$ and p in the AR model, where m is number of differences, m=sIinitial.GetLength(1) :

$\phi_p(B)(\Delta_{s_1}^{d_1}\Delta_{s_2}^{d_2} \ldots\Delta_{s_m}^{d_m}Z_t-\mu) = a_t\rm{,}$

where $\{Z_t\}$ is the original time series, B is the backward shift operator defined by $B^kZ_t=Z_{t-k} \rm{, \,\,with }\,\, k\ge0$ ,

is Gaussian white noise with

and $\mbox{Var}[a_t]= \sigma^2$ , $\phi_p(B)= 1-\phi_1B - \phi_2B^2 - \cdots - \phi_pB^p,\,\,\,\, 0\le{p}\le\rm{maxlag}$ , $\Delta_s^d=(1-B^s)^d$ , with $s \gt 0, d \ge 0$ , and $\mu$ is a centering parameter for the differenced series.

Reference

ARSeasonalFit Class

Imsl.Stat Namespace