| ConjugateGradient Class |
Namespace: Imsl.Math
Assembly: ImslCS (in ImslCS.dll) Version: 6.5.2.0
The ConjugateGradient type exposes the following members.
| Name | Description | |
|---|---|---|
| ConjugateGradient |
Conjugate gradient constructor.
|
| Name | Description | |
|---|---|---|
| Equals | Determines whether the specified object is equal to the current object. (Inherited from Object.) | |
| Finalize | Allows an object to try to free resources and perform other cleanup operations before it is reclaimed by garbage collection. (Inherited from Object.) | |
| GetHashCode | Serves as a hash function for a particular type. (Inherited from Object.) | |
| GetJacobi |
Returns the Jacobi preconditioning matrix.
| |
| GetType | Gets the Type of the current instance. (Inherited from Object.) | |
| MemberwiseClone | Creates a shallow copy of the current Object. (Inherited from Object.) | |
| SetJacobi |
Defines a Jacobi preconditioner as the preconditioning matrix, that is, M is
the diagonal of A.
| |
| Solve |
Solves a real symmetric positive or negative definite system | |
| ToString | Returns a string that represents the current object. (Inherited from Object.) |
| Name | Description | |
|---|---|---|
| Iterations |
The number of iterations needed by the conjugate gradient algorithm.
| |
| MaxIterations | The maximum number of iterations allowed.
| |
| RelativeError |
The relative error used for stopping the algorithm.
|
Class ConjugateGradient solves the symmetric positive or negative
definite linear system ![]() using the conjugate
gradient method with optional preconditioning. This method is described
in detail by Golub and Van Loan (1983, Chapter 10), and in Hageman and
Young (1981, Chapter 7).
using the conjugate
gradient method with optional preconditioning. This method is described
in detail by Golub and Van Loan (1983, Chapter 10), and in Hageman and
Young (1981, Chapter 7).
The preconditioning matrix M is a matrix that approximates A,
and for which the linear system Mz=r is easy to solve. These two
properties are in conflict; balancing them is a topic of current research.
If no preconditioning matrix is specified, ![]() is set to the
identity, i.e.
is set to the
identity, i.e. ![]() .
.
The number of iterations needed depends on the matrix and the error tolerance. As a rough guide,
Let M be the preconditioning matrix, let b,p,r,x and z be
vectors and let ![]() be the desired relative error. Then the
algorithm used is as follows:
be the desired relative error. Then the
algorithm used is as follows:
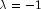
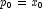
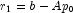
- for

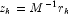
- if
 then
then 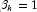

- else
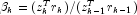
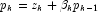
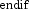
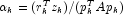
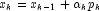
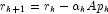
- if
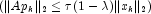 then
then - recompute

- if
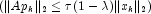 exit
exit - endif
- endfor
Here, ![]() is an estimate of
is an estimate of ![]() ,
the largest eigenvalue of the iteration matrix
,
the largest eigenvalue of the iteration matrix ![]() . The stopping criterion
is based on the result (Hageman and Young 1981, pp. 148-151)
. The stopping criterion
is based on the result (Hageman and Young 1981, pp. 148-151)
![T_l = \left[ \begin{array}{ccccc}
\mu_1 & \omega_2 & & & \\
\omega_2 & \mu_2 & \omega_3 & & \\
& \omega_3 & \mu_3 & \raisebox{-1ex}{$\ddots$} & \\
& & \ddots & \ddots & \omega_l \\
& & & \omega_l & \mu_l
\end{array} \right]](eqn/eqn_1026.png)
Usually, the eigenvalue computation is needed for only a few of the iterations.