| CsTCB Class |
Namespace: Imsl.Math
Assembly: ImslCS (in ImslCS.dll) Version: 6.5.2.0
The CsTCB type exposes the following members.
| Name | Description | |
|---|---|---|
| CsTCB | Constructs the tension-continuity-bias (TCB) cubic spline interpolant to the given
data points.
|
| Name | Description | |
|---|---|---|
| Compute | Computes the tension-continuity-bias (TCB) cubic spline interpolant.
| |
| Derivative(Double) |
Returns the value of the first derivative of the spline at a point.
(Inherited from Spline.) | |
| Derivative(Double, Int32) |
Returns the value of the derivative of the spline at a point.
(Inherited from Spline.) | |
| Derivative(Double, Int32) |
Returns the value of the derivative of the spline at each point of an
array.
(Inherited from Spline.) | |
| Equals | Determines whether the specified object is equal to the current object. (Inherited from Object.) | |
| Eval(Double) |
Returns the value of the spline at a point.
(Inherited from Spline.) | |
| Eval(Double) |
Returns the value of the spline at each point of an array.
(Inherited from Spline.) | |
| Finalize | Allows an object to try to free resources and perform other cleanup operations before it is reclaimed by garbage collection. (Inherited from Object.) | |
| GetBreakpoints |
Returns a copy of the breakpoints.
(Inherited from Spline.) | |
| GetHashCode | Serves as a hash function for a particular type. (Inherited from Object.) | |
| GetType | Gets the Type of the current instance. (Inherited from Object.) | |
| Integral |
Returns the value of an integral of the spline.
(Inherited from Spline.) | |
| MemberwiseClone | Creates a shallow copy of the current Object. (Inherited from Object.) | |
| SetBias | Sets the bias values at the data points.
| |
| SetContinuity | Sets the continuity values at the data points.
| |
| SetTension | Sets the tension values at the data points.
| |
| ToString | Returns a string that represents the current object. (Inherited from Object.) |
| Name | Description | |
|---|---|---|
| LeftEndTangent | The value of the tangent at the leftmost endpoint.
| |
| RightEndTangent | The value of the tangent at the rightmost endpoint.
|
Let ![]() xData,
xData, ![]() yData,
and
yData,
and ![]() the length of xData and yData.
Class CsTCB computes the Kochanek-Bartels spline, a piecewise
cubic Hermite spline interpolant to the set of data points
the length of xData and yData.
Class CsTCB computes the Kochanek-Bartels spline, a piecewise
cubic Hermite spline interpolant to the set of data points ![]() for
for ![]() . The breakpoints of the spline are the abscissas.
As with all of the univariate interpolation functions, the abscissas need not be sorted.
. The breakpoints of the spline are the abscissas.
As with all of the univariate interpolation functions, the abscissas need not be sorted.
The ![]() values are the knots, so the
values are the knots, so the ![]() -th
interval is
-th
interval is ![]() . (To simplify the explanation, it is
assumed that the data points are given in increasing order.) The cubic Hermite in the
. (To simplify the explanation, it is
assumed that the data points are given in increasing order.) The cubic Hermite in the
![]() -th segment has a starting value of
-th segment has a starting value of ![]() and an
ending value of
and an
ending value of ![]() . Its incoming tangent is
. Its incoming tangent is
The value of the tangent at the right endpoint is given as:
By default the values of the tangents at the leftmost and rightmost endpoints are zero. These values can be reset via the LeftEndTangent and RightEndTangent properties.
The spline has a continuous first derivative (![]() ) if at each data
point the left and right tangents are equal. This is true if the continuity parameters,
) if at each data
point the left and right tangents are equal. This is true if the continuity parameters, ![]() , are
all zero. For any values of the parameters the spline is continuous (
, are
all zero. For any values of the parameters the spline is continuous (![]() ).
).
If ![]() for all
for all ![]() , then the curve is the Catmull-Rom
spline.
, then the curve is the Catmull-Rom
spline.
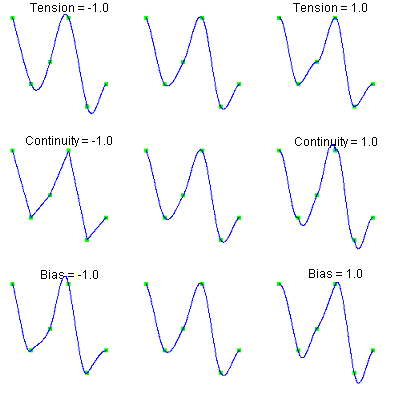
The following chart shows the same data points interpolated with different parameter values. All of the tension, continuity, and bias parameters are zero except for the labeled parameter, which has the indicated value at all data points.
Tension controls how sharply the spline bends at the data points. The tension values can be set via the SetTension method. If tension values are near +1, the curve tightens. If the tension values are near -1, the curve slackens.
The continuity parameter controls the continuity of the first derivative. The continuity values
can be set via the SetContinuity method. If the continuity value is zero, the
spline's first derivative is continuous, so the spline is ![]() .
.
The bias parameter controls the weighting of the left and right tangents. If zero, the tangents are equally weighted. If the bias parameter is near +1, the left tangent dominates. If the bias parameter is near -1, the right tangent dominates. The bias values can be set via the SetBias method.