MinConNLP Class

MinConNLP Class

General nonlinear programming solver.

Inheritance Hierarchy

System.Object
Imsl.Math.MinConNLP

Namespace: Imsl.Math
Assembly: ImslCS (in ImslCS.dll) Version: 6.5.2.0

Syntax

C++

Copy

[SerializableAttribute]
public class MinConNLP

<SerializableAttribute>
Public Class MinConNLP

[SerializableAttribute]
public ref class MinConNLP

[<SerializableAttribute>]
type MinConNLP =  class end

The MinConNLP type exposes the following members.

Constructors

	Name	Description
	MinConNLP	Nonlinear programming solver constructor.

Top

Methods

	Name	Description
	Equals	Determines whether the specified object is equal to the current object. (Inherited from Object.)
	Finalize	Allows an object to try to free resources and perform other cleanup operations before it is reclaimed by garbage collection. (Inherited from Object.)
	GetConstraintResiduals	Returns the constraint residuals.
	GetHashCode	Serves as a hash function for a particular type. (Inherited from Object.)
	GetLagrangeMultiplierEst	Returns the Lagrange multiplier estimates of the constraints.
	GetSolution	Returns the last computed solution.
	GetType	Gets the Type of the current instance. (Inherited from Object.)
	MemberwiseClone	Creates a shallow copy of the current Object. (Inherited from Object.)
	SetGuess	Sets the initial guess of the minimum point of the input function.
	SetXlowerBound	Sets the lower bounds on the variables.
	SetXscale	The internal scaling of the variables.
	SetXupperBound	Sets the upper bounds on the variables.
	Solve	Solve a general nonlinear programming problem using the successive quadratic programming algorithm with a finite-difference gradient or with a user-supplied gradient.
	ToString	Returns a string that represents the current object. (Inherited from Object.)

Top

Properties

	Name	Description
	BindingThreshold	The binding threshold for constraints.
	BoundViolationBound	The amount by which bounds may be violated during numerical differentiation.
	DifferentiationType	The type of numerical differentiation to be used.
	FunctionPrecision	The relative precision of the function evaluation routine.
	GradientPrecision	The relative precision in gradients.
	MaximumIterations	The maximum number of iterations allowed.
	MultiplierError	The error allowed in the multipliers.
	NumberOfProcessors	Perform the parallel calculations with the maximum possible number of processors set to NumberOfProcessors.
	Parallel	Enable or disable performing MinConNLP.IFunction.F in parallel.
	PenaltyBound	The universal bound for describing how much the unscaled penalty-term may deviate from zero.
	ScalingBound	The scaling bound for the internal automatic scaling of the objective function.
	ViolationBound	Defines allowable constraint violations of the final accepted result.

Top

Remarks

MinConNLP is based on the FORTRAN subroutine, DONLP2, by Peter Spellucci and licensed from TU Darmstadt. MinConNLP uses a sequential equality constrained quadratic programming method with an active set technique, and an alternative usage of a fully regularized mixed constrained subproblem in case of nonregular constraints (i.e. linear dependent gradients in the "working sets"). It uses a slightly modified version of the Pantoja-Mayne update for the Hessian of the Lagrangian, variable dual scaling and an improved Armjijo-type stepsize algorithm. Bounds on the variables are treated in a gradient-projection like fashion. Details may be found in the following two papers:

P. Spellucci: An SQP method for general nonlinear programs using only equality constrained subproblems. Math. Prog. 82, (1998), 413-448.

P. Spellucci: A new technique for inconsistent problems in the SQP method. Math. Meth. of Oper. Res. 47, (1998), 355-500. (published by Physica Verlag, Heidelberg, Germany).

The problem is stated as follows:

$\mathop {\min }\limits_{x\; \in \;R^n } f\left ( x \right)$

subject to

${\rm{ }}g_j \left( x \right) = 0, {\rm{for}} \,\, j = 1,\; \ldots ,\;m_e$

$g_j \left( x \right) \ge 0, \rm{for} \,\, {j = m_e + 1,\; \ldots ,\;m}$

$x_l \le x \le x_u$

where all problem functions are assumed to be continuously differentiable. Although default values are provided for optional input arguments, it may be necessary to adjust these values for some problems. Through the use of member functions, MinConNLP allows for several parameters of the algorithm to be adjusted to account for specific characteristics of problems. The DONLP2 Users Guide provides detailed descriptions of these parameters as well as strategies for maximizing the performance of the algorithm. In addition, the following are a number of guidelines to consider when using MinConNLP:

A good initial starting point is very problem specific and should be provided by the calling program whenever possible. See method SetGuess.
Gradient approximation methods can have an effect on the success of MinConNLP. Selecting a higher order approximation method may be necessary for some problems. See property DifferentiationType.
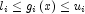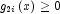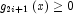If a two sided constraint $l_i \le g_i \left( x \right) \le u_i$ is transformed into two constraints, $g_{2i} \left( x \right) \ge 0$ and $g_{2i+1} \left( x \right) \ge 0$ , then choose 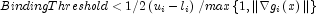$BindingThreshold \lt 1/2 \left( u_i-l_i \right)/max \left\{ 1,\|\nabla g_i \left( x \right) \| \right\}$ , or at least try to provide an estimate for that value. This will increase the efficiency of the algorithm. See property BindingThreshold.
The parameter ierr provided in the interface to the user supplied function F can be very useful in cases when evaluation is requested at a point that is not possible or reasonable. For example, if evaluation at the requested point would result in a floating point exception, then setting ierr to true and returning without performing the evaluation will avoid the exception. MinConNLP will then reduce the stepsize and try the step again. Note, if ierr is set to true for the initial guess, then an error is issued.

Reference

Imsl.Math Namespace

Other Resources

Finite-difference Example

Gradient Example