| SparseCholesky Class |
Namespace: Imsl.Math
Assembly: ImslCS (in ImslCS.dll) Version: 6.5.2.0
The SparseCholesky type exposes the following members.
| Name | Description | |
|---|---|---|
| SparseCholesky |
Constructs the matrix structure for the Cholesky factorization of
a sparse symmetric positive definite matrix of type SparseMatrix.
|
| Name | Description | |
|---|---|---|
| Equals | Determines whether the specified object is equal to the current object. (Inherited from Object.) | |
| FactorNumerically |
Computes the numeric factorization of a sparse real symmetric positive
definite matrix.
| |
| FactorSymbolically |
Computes the symbolic factorization of a sparse real symmetric positive definite matrix.
| |
| Finalize | Allows an object to try to free resources and perform other cleanup operations before it is reclaimed by garbage collection. (Inherited from Object.) | |
| GetHashCode | Serves as a hash function for a particular type. (Inherited from Object.) | |
| GetNumericFactor | Returns the numeric Cholesky factor.
| |
| GetSymbolicFactor |
Returns the symbolic Cholesky factor.
| |
| GetType | Gets the Type of the current instance. (Inherited from Object.) | |
| MemberwiseClone | Creates a shallow copy of the current Object. (Inherited from Object.) | |
| SetNumericFactor | Sets the numeric Cholesky factor to use in solving of a sparse
positive definite system of linear equations | |
| SetSymbolicFactor |
Sets the symbolic Cholesky factor to use in solving a sparse
positive definite system of linear equations | |
| Solve |
Computes the solution of a sparse real symmetric positive definite system of linear
equations | |
| ToString | Returns a string that represents the current object. (Inherited from Object.) |
| Name | Description | |
|---|---|---|
| LargestDiagonalElement |
The largest diagonal element of the Cholesky factor.
| |
| NumberOfNonzeros |
The number of nonzeros in the Cholesky factor.
| |
| NumericFactorizationMethod |
The method used in the numerical factorization of the permuted
input matrix.
| |
| SmallestDiagonalElement |
The smallest diagonal element of the Cholesky factor.
|
Class SparseCholesky computes the Cholesky factorization of a
sparse symmetric positive definite matrix A. This factorization can
then be used to compute the solution of the linear system
![]() .
.
Typically, the solution of a large sparse positive definite system
![]() is done in 4 steps:
is done in 4 steps:
- In step one, an ordering algorithm is used to preserve sparsity in the Cholesky factor L of matrix A during the numerical factorization process. The new order can be described by a permutation matrix P.
- Step two consists of
setting up the data structure for the Cholesky factor L, where
 . This step is called the symbolic
factorization phase of the computation. During symbolic factorization, only
the sparsity pattern of sparse matrix A, i.e., the locations of the
nonzero entries of matrix A are needed but not any of the elements
themselves.
. This step is called the symbolic
factorization phase of the computation. During symbolic factorization, only
the sparsity pattern of sparse matrix A, i.e., the locations of the
nonzero entries of matrix A are needed but not any of the elements
themselves. - In step 3, the numerical factorization phase, the Cholesky factorization is done numerically.
- Step 4 is the solution phase.
Here, the numerical solution, x, to the original system is obtained
by solving the two triangular systems
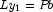 ,
,
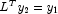 and the permutation
and the permutation
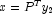 .
.
Class SparseCholesky realizes all four steps by algorithms described in George and Liu (1981). Especially, step one, is a realization of a minimum degree ordering algorithm. The numerical factorization in its standard form is based on a sparse compressed storage scheme. Alternatively, a multifrontal method can be used. The multifrontal method requires more storage but will be faster than the standard method in certain cases. The multifrontal method is based on the routines in Liu (1987). For a detailed description of this method, see Liu (1990), also Duff and Reid(1983, 1984), Ashcraft (1987) et al. (1987), and Liu (1986, 1989, 1992).The numerical factorization method can be specified by using the NumericFactorizationMethod property.
The Solve method will compute the symbolic and numeric factorizations if they have not already been computed or supplied by the user through FactorSymbolically, FactorNumerically, SetNumericFactor, or SetSymbolicFactor. These factorizations are retained for later use by the Solve method when different right-hand sides are to be solved.
There is a special situation where computations can be simplified. If an application generates different sparse symmetric positive definite coefficient matrices that all have the same sparsity pattern, then by using SetSymbolicFactor the symbolic factorization need only be computed once.