| AutoCorrelation Class |
Namespace: Imsl.Stat
Assembly: ImslCS (in ImslCS.dll) Version: 6.5.2.0
The AutoCorrelation type exposes the following members.
| Name | Description | |
|---|---|---|
| AutoCorrelation |
Constructor to compute the sample autocorrelation function of a
stationary time series.
|
| Name | Description | |
|---|---|---|
| Equals | Determines whether the specified object is equal to the current object. (Inherited from Object.) | |
| Finalize | Allows an object to try to free resources and perform other cleanup operations before it is reclaimed by garbage collection. (Inherited from Object.) | |
| GetAutoCorrelations |
Returns the autocorrelations of the time series x.
| |
| GetAutoCovariances |
Returns the variance and autocovariances of the time series x.
| |
| GetHashCode | Serves as a hash function for a particular type. (Inherited from Object.) | |
| GetPartialAutoCorrelations |
Returns the sample partial autocorrelation function of the stationary
time series x.
| |
| GetStandardErrors |
Returns the standard errors of the autocorrelations of the
time series x.
| |
| GetType | Gets the Type of the current instance. (Inherited from Object.) | |
| MemberwiseClone | Creates a shallow copy of the current Object. (Inherited from Object.) | |
| ToString | Returns a string that represents the current object. (Inherited from Object.) |
| Name | Description | |
|---|---|---|
| Mean |
The mean of the time series x.
| |
| NumberOfProcessors |
Perform the parallel calculations with the maximum possible number of
processors set to NumberOfProcessors.
| |
| Variance |
Returns the variance of the time series x.
|
AutoCorrelation estimates the autocorrelation function of a
stationary time series given a sample of n observations
![]() for
for
![]() .
.
Let
where K = maximumLag. Note that
![]() is an estimate of the sample
variance. The autocorrelation function
is an estimate of the sample
variance. The autocorrelation function ![]() is
estimated by
is
estimated by
Note that ![]() by definition.
by definition.
The standard errors of sample autocorrelations may be optionally computed according to the GetStandardErrors method argument stderrMethod. One method (Bartlett 1946) is based on a general asymptotic expression for the variance of the sample autocorrelation coefficient of a stationary time series with independent, identically distributed normal errors. The theoretical formula is
where ![]() assumes
assumes ![]() is unknown. For computational purposes, the autocorrelations
is unknown. For computational purposes, the autocorrelations
![]() are replaced by their estimates
are replaced by their estimates
![]() for
for ![]() ,
and the limits of summation are bounded because of the assumption that
,
and the limits of summation are bounded because of the assumption that
![]() for all
for all ![]() such
that
such
that ![]() .
.
A second method (Moran 1947) utilizes an exact formula for the variance of the sample autocorrelation coefficient of a random process with independent, identically distributed normal errors. The theoretical formula is
where ![]() is assumed to be equal to zero. Note that
this formula does not depend on the autocorrelation function.
is assumed to be equal to zero. Note that
this formula does not depend on the autocorrelation function.
The method GetPartialAutoCorrelations returns the estimated
partial autocorrelations of the stationary time series given K =
maximumLag sample autocorrelations ![]() for k=0,1,...,K. Consider the AR(k) process defined by
for k=0,1,...,K. Consider the AR(k) process defined by
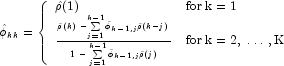
This procedure is sensitive to rounding error and should not be used if
the parameters are near the nonstationarity boundary. A possible
alternative would be to estimate ![]() for successive AR(k) models using least or maximum likelihood.
Based on the hypothesis that the true process is AR(p), Box and
Jenkins (1976, page 65) note
for successive AR(k) models using least or maximum likelihood.
Based on the hypothesis that the true process is AR(p), Box and
Jenkins (1976, page 65) note
See Box and Jenkins (1976, pages 82-84) for more information concerning the partial autocorrelation function.