| NonlinearRegression Class |
Namespace: Imsl.Stat
Assembly: ImslCS (in ImslCS.dll) Version: 6.5.2.0
The NonlinearRegression type exposes the following members.
| Name | Description | |
|---|---|---|
| NonlinearRegression |
Constructs a new nonlinear regression object.
|
| Name | Description | |
|---|---|---|
| Equals | Determines whether the specified object is equal to the current object. (Inherited from Object.) | |
| Finalize | Allows an object to try to free resources and perform other cleanup operations before it is reclaimed by garbage collection. (Inherited from Object.) | |
| GetCoefficient |
Returns the estimate for a coefficient.
| |
| GetHashCode | Serves as a hash function for a particular type. (Inherited from Object.) | |
| GetSSE |
Returns the sums of squares for error.
| |
| GetType | Gets the Type of the current instance. (Inherited from Object.) | |
| MemberwiseClone | Creates a shallow copy of the current Object. (Inherited from Object.) | |
| Solve |
Solves the least squares problem and returns the regression
coefficients.
| |
| ToString | Returns a string that represents the current object. (Inherited from Object.) |
| Name | Description | |
|---|---|---|
| AbsoluteTolerance |
The absolute function tolerance.
| |
| Coefficients |
The regression coefficients.
| |
| DFError |
The degrees of freedom for error.
| |
| Digits |
The number of good digits in the residuals.
| |
| ErrorStatus |
Characterizes the performance of NonlinearRegression.
| |
| FalseConvergenceTolerance |
The false convergence tolerance.
| |
| GradientTolerance |
The gradient tolerance.
| |
| Guess |
The initial guess of the parameter values.
| |
| InitialTrustRegion |
The initial trust region radius.
| |
| MaxIterations |
The maximum number of iterations allowed during optimization
| |
| MaxStepsize |
The maximum allowable stepsize.
| |
| R |
A copy of the R matrix.
| |
| Rank |
The rank of the matrix.
| |
| RelativeTolerance |
The relative function tolerance
| |
| Scale |
The scaling array for theta.
| |
| StepTolerance |
The step tolerance.
|
The nonlinear regression model is
where the observed values of the ![]() constitute the
responses or values of the dependent variable, the known
constitute the
responses or values of the dependent variable, the known ![]() are vectors of values of the independent (explanatory)
variables,
are vectors of values of the independent (explanatory)
variables, ![]() is the vector of
is the vector of ![]() regression parameters, and the
regression parameters, and the ![]() are independently distributed normal errors each with mean
zero and variance
are independently distributed normal errors each with mean
zero and variance ![]() . For this model, a least
squares estimate of
. For this model, a least
squares estimate of ![]() is also a maximum
likelihood estimate of
is also a maximum
likelihood estimate of ![]() .
.
The residuals for the model are
NonlinearRegression is based on MINPACK routines LMDIF and
LMDER by More' et al. (1980). NonlinearRegression uses a
modified Levenberg-Marquardt method to generate a sequence of
approximations to the solution. Let ![]() be
the current estimate of
be
the current estimate of ![]() . A new estimate is
given by
. A new estimate is
given by
The algorithm uses a "trust region" approach with a step bound of
![]() . A solution of the equations is first
obtained for
. A solution of the equations is first
obtained for ![]() . If
. If ![]() , this update is accepted; otherwise,
, this update is accepted; otherwise, ![]() is set to a positive value and another solution is obtained.
The method is discussed by Levenberg (1944), Marquardt (1963), and
Dennis and Schnabel (1983, pages 129 - 147, 218 - 338).
is set to a positive value and another solution is obtained.
The method is discussed by Levenberg (1944), Marquardt (1963), and
Dennis and Schnabel (1983, pages 129 - 147, 218 - 338).
Forward finite differences are used to estimate the Jacobian numerically unless the user supplied function computes the derivatives. In this case the Jacobian is computed analytically via the user-supplied function.
NonlinearRegression does not actually store the Jacobian but uses fast Givens transformations to construct an orthogonal reduction of the Jacobian to upper triangular form. The reduction is based on fast Givens transformations (see Golub and Van Loan 1983, pages 156-162, Gentleman 1974). This method has two main advantages:
- The loss of accuracy resulting from forming the crossproduct matrix
used in the equations for
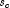 is avoided.
is avoided. - The n x p Jacobian need not be stored saving space
when
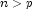 .
.
A weighted least squares fit can also be performed. This is appropriate
when the variance of ![]() in the nonlinear
regression model is not constant but instead is
in the nonlinear
regression model is not constant but instead is ![]() . Here,
. Here, ![]() are weights input via the
user supplied function. For the weighted case, NonlinearRegression
finds the estimate by minimizing a weighted sum of squares error.
are weights input via the
user supplied function. For the weighted case, NonlinearRegression
finds the estimate by minimizing a weighted sum of squares error.
Nonlinear regression allows users to specify the model's functional form. This added flexibility can cause unexpected convergence problems for users who are unaware of the limitations of the algorithm. Also, in many cases, there are possible remedies that may not be immediately obvious. The following is a list of possible convergence problems and some remedies. No one-to-one correspondence exists between the problems and the remedies. Remedies for some problems may also be relevant for the other problems.
- A local minimum is found. Try a different starting value. Good
starting values can often be obtained by fitting simpler models. For
example, for a nonlinear function
good starting values can be obtained from the estimated linear regression coefficients
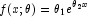
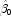 and
and
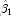 from a simple linear regression of
ln y on ln x. The starting values for the nonlinear
regression in this case would be
If an approximate linear model is unclear, then simplify the model by reducing the number of nonlinear regression parameters. For example, some nonlinear parameters for which good starting values are known could be set to these values. This simplifies the approach to computing starting values for the remaining parameters.
from a simple linear regression of
ln y on ln x. The starting values for the nonlinear
regression in this case would be
If an approximate linear model is unclear, then simplify the model by reducing the number of nonlinear regression parameters. For example, some nonlinear parameters for which good starting values are known could be set to these values. This simplifies the approach to computing starting values for the remaining parameters.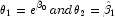
- The estimate of
 is incorrectly returned
as the same or very close to the initial estimate.
is incorrectly returned
as the same or very close to the initial estimate.
- The scale of the problem may be orders of magnitude
smaller than the assumed default of 1 causing premature stopping. For
example, if the sums of squares for error is less than approximately
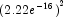 , the routine stops. See Example
3, which shows how to shut down some of the stopping criteria that may
not be relevant for your particular problem and which also shows how to
improve the speed of convergence by the input of the scale of the model
parameters.
, the routine stops. See Example
3, which shows how to shut down some of the stopping criteria that may
not be relevant for your particular problem and which also shows how to
improve the speed of convergence by the input of the scale of the model
parameters. - The scale of the problem may be orders of magnitude larger than the assumed default causing premature stopping. The information with regard to the input of the scale of the model parameters in Example 3 is also relevant here. In addition, the maximum allowable step size MaxStepsize in Example 3 may need to be increased.
- The residuals are input with accuracy much less than machine accuracy, causing premature stopping because a local minimum is found. Again see Example 3 to see how to change some default tolerances. If you cannot improve the precision of the computations of the residual, you need to use method Digits to indicate the actual number of good digits in the residuals.
- The scale of the problem may be orders of magnitude
smaller than the assumed default of 1 causing premature stopping. For
example, if the sums of squares for error is less than approximately
- The model is discontinuous as a function of
 . There may be a mistake in the user-supplied function. Note
that the function
. There may be a mistake in the user-supplied function. Note
that the function 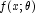 can be a
discontinuous function of x.
can be a
discontinuous function of x. - The R matrix value given by R is inaccurate. If only a function is supplied try providing the NonlinearRegressionIDerivative. If the derivative is supplied try providing only NonlinearRegressionIFunction.
- Overflow occurs during the computations. Make sure the user-supplied
functions do not overflow at some value of
 .
.
- The estimate of
 is going to infinity. A
parameterization of the problem in terms of reciprocals may help.
is going to infinity. A
parameterization of the problem in terms of reciprocals may help. - Some components of
 are outside known
bounds. This can sometimes be handled by making a function that produces
artificially large residuals outside of the bounds (even though this
introduces a discontinuity in the model function).
are outside known
bounds. This can sometimes be handled by making a function that produces
artificially large residuals outside of the bounds (even though this
introduces a discontinuity in the model function).
Note that the Solve(NonlinearRegressionIFunction) method must be called before using any property as a right operand, otherwise the value is null.