| SelectionRegression Class |
Namespace: Imsl.Stat
Assembly: ImslCS (in ImslCS.dll) Version: 6.5.2.0
The SelectionRegression type exposes the following members.
| Name | Description | |
|---|---|---|
| SelectionRegression |
Constructs a new SelectionRegression object.
|
| Name | Description | |
|---|---|---|
| Compute(Double, Double) |
Computes the best multiple linear regression models.
| |
| Compute(Double, Int32) |
Computes the best multiple linear regression models using a
user-supplied covariance matrix.
| |
| Compute(Double, Double, Double) |
Computes the best weighted multiple linear regression models.
| |
| Compute(Double, Double, Double, Double) |
Computes the best weighted multiple linear regression models using
frequencies for each observation.
| |
| Equals | Determines whether the specified object is equal to the current object. (Inherited from Object.) | |
| Finalize | Allows an object to try to free resources and perform other cleanup operations before it is reclaimed by garbage collection. (Inherited from Object.) | |
| GetHashCode | Serves as a hash function for a particular type. (Inherited from Object.) | |
| GetType | Gets the Type of the current instance. (Inherited from Object.) | |
| MemberwiseClone | Creates a shallow copy of the current Object. (Inherited from Object.) | |
| ToString | Returns a string that represents the current object. (Inherited from Object.) |
| Name | Description | |
|---|---|---|
| CriterionOption |
The criterion option used to calculate the regression estimates.
| |
| MaximumBestFound |
The maximum number of best regressions to be found.
| |
| MaximumGoodSaved |
The maximum number of good regressions for each subset size saved.
| |
| MaximumSubsetSize |
The maximum subset size if | |
| Statistics |
A SummaryStatistics object.
|
Class SelectionRegression finds the best subset regressions for a regression problem with three or more independent variables. Typically, the intercept is forced into all models and is not a candidate variable. In this case, a sum-of-squares and crossproducts matrix for the independent and dependent variables corrected for the mean is computed internally. Optionally, SelectionRegression supports user-calculated sum-of-squares and crossproducts matrices; see the description of the Compute(Double, Double) method.
"Best" is defined by using one of the following three criteria:
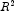 (in percent)
(in percent) 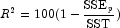
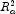 (adjusted
(adjusted 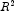 )
Note that maximizing the
)
Note that maximizing the![R^2_a=100[1-(\frac{n-1}{n-p})\frac{{\mbox{SSE}}_p}{\mbox{SST}}]](eqn/eqn_3884.png)
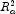 is equivalent to
minimizing the residual mean squared error:
is equivalent to
minimizing the residual mean squared error:
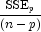
- Mallow's
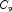 statistic
statistic
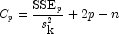
Here, n is equal to the sum of the frequencies (or the number of
rows in x if frequencies are not specified in the
Compute method), and ![]() is the total
sum-of-squares. k is the number of candidate or independent
variables, represented as the nCandidate argument in
the SelectionRegression constructor.
is the total
sum-of-squares. k is the number of candidate or independent
variables, represented as the nCandidate argument in
the SelectionRegression constructor. ![]() is the error sum-of-squares in a model containing p
regression parameters including
is the error sum-of-squares in a model containing p
regression parameters including ![]() (or
p - 1 of the k candidate variables). Variable
(or
p - 1 of the k candidate variables). Variable
Class SelectionRegression is based on the algorithm of Furnival and Wilson (1974). This algorithm finds the maximum number of good saved candidate regressions for each possible subset size. For more details, see method MaximumGoodSaved. These regressions are used to identify a set of best regressions. In large problems, many regressions are not computed. They may be rejected without computation based on results for other subsets; this yields an efficient technique for considering all possible regressions.
There are cases when the user may want to input the variance-covariance matrix rather than allow it to be calculated. This can be accomplished using the appropriate Compute method. Three situations in which the user may want to do this are as follows:
- The intercept is not in the model. A raw (uncorrected) sum of
squares and crossproducts matrix for the independent and dependent
variables is required. Argument nObservations must be
set to 1 greater than the number of observations. Form
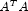 , where A = [A, Y], to compute the raw sum-of-squares
and crossproducts matrix.
, where A = [A, Y], to compute the raw sum-of-squares
and crossproducts matrix. - An intercept is a candidate variable. A raw (uncorrected) sum of squares and crossproducts matrix for the constant regressor (= 1.0), independent, and dependent variables is required for cov. In this case, cov contains one additional row and column corresponding to the constant regressor. This row and column contain the sum-of-squares and crossproducts of the constant regressor with the independent and dependent variables. The remaining elements in cov are the same as in the previous case. Argument nObservations must be set to 1 greater than the number of observations.
- There are m variables that must be forced into the models. A sum-of-squares and crossproducts matrix adjusted for the m variables is required (calculated by regressing the candidate variables on the variables to be forced into the model). Argument nObservations must be set to m less than the number of observations.
SelectionRegression can save considerable CPU time over explicitly computing all possible regressions. However, the function has some limitations that can cause unexpected results for users who are unaware of the limitations of the software.
- For
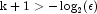 , where
, where
 is the largest relative spacing for double
precision, some results can be incorrect. This limitation arises because
the possible models indicated (the model numbers 1, 2, ..., 2k)
are stored as floating-point values; for sufficiently large k,
the model numbers cannot be stored exactly. On many computers, this
means SelectionRegression (for
is the largest relative spacing for double
precision, some results can be incorrect. This limitation arises because
the possible models indicated (the model numbers 1, 2, ..., 2k)
are stored as floating-point values; for sufficiently large k,
the model numbers cannot be stored exactly. On many computers, this
means SelectionRegression (for  )
can produce incorrect results.
)
can produce incorrect results. - SelectionRegression eliminates some subsets of candidate variables by obtaining lower bounds on the error sum-of-squares from fitting larger models. First, the full model containing all independent variables is fit sequentially using a forward stepwise procedure in which one variable enters the model at a time, and criterion values and model numbers for all the candidate variables that can enter at each step are stored. If linearly dependent variables are removed from the full model, a "VariablesDeleted" warning is issued. In this case, some submodels that contain variables removed from the full model because of linear dependency can be overlooked if they have not already been identified during the initial forward stepwise procedure. If this warning is issued and you want the variables that were removed from the full model to be considered in smaller models, you can rerun the program with a set of linearly independent variables.