| BesselJ Method (Double, Double, Int32) |
Evaluate a sequence of Bessel functions of the first kind with real
order and real positive argument.
Namespace: Imsl.Math
Assembly: ImslCS (in ImslCS.dll) Version: 6.5.2.0
Parameters
- xnu
- Type: SystemDouble
A double representing the lowest order desired. xnu must be at least zero and less than 1. - x
- Type: SystemDouble
A double representing the argument for which the sequence of Bessel functions is to be evaluated. - n
- Type: SystemInt32
A int representing the order of the last element in the sequence. If order is the highest order desired, set n to int(order).
Return Value
Type: DoubleA double array of length n+1 containing the values of the function through the series. Bessel.J[I] contains the value of the Bessel function of order I + v at x for I=0 to n.
The Bessel function 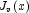 , is defined to be
, is defined to be
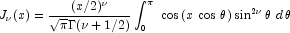 This code is based on the work of Gautschi (1964) and Skovgaard
(1975). It uses backward recursion.
This code is based on the work of Gautschi (1964) and Skovgaard
(1975). It uses backward recursion.