besselK0¶

Evaluates the real modified Bessel function of the second kind of order zero \(K_0\)(x).

Synopsis¶

besselK0 (x)

Required Arguments¶

float x (Input): Point at which the modified Bessel function is to be evaluated. It must be positive.

Return Value¶

The value of the modified Bessel function

\[K_0(x) = \int_0^{\infty} \cos (x \sinh t) dt\]

If no solution can be computed, then NaN is returned.

Description¶

Since \(K_0(x)\) is complex for negative x and is undefined at \(x=0\), besselK0 is defined only for \(x>0\). For large x, besselK0 will underflow.

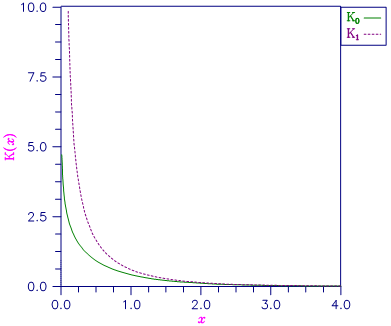
Figure 9.19 — Plot of \(K_0(x)\) and \(K_1(x)\)

Example¶

The Bessel function \(K_0(1.5)\) is evaluated.

from __future__ import print_function
from numpy import *
from pyimsl.math.besselK0 import besselK0

x = 1.5
ans = besselK0(x)
print("K0(%f) = %f" % (x, ans))

Output¶

K0(1.500000) = 0.213806

Alert Errors¶

IMSL_LARGE_ARG_UNDERFLOW The argument x must not be so large that the result, approximately equal to \(\sqrt{\pi/(2x)} e^{-x}\), underflows.