beta¶

Evaluates the real beta function \(\beta(x,y)\).

Synopsis¶

beta (x, y)

Required Arguments¶

float x (Input): Point at which the beta function is to be evaluated. It must be positive.
float y (Input): Point at which the beta function is to be evaluated. It must be positive.

Return Value¶

The value of the beta function \(\beta(x,y)\). If no result can be computed, NaN is returned.

Description¶

The beta function, \(\beta(x,y)\), is defined to be

\[\beta(x,y) = \frac{\mathit{\Gamma}(x)\mathit{\Gamma}(y)}{\mathit{\Gamma}(x+y)} = \int_0^1 t^{x-1} (1-t)^{y-1} dt\]

The beta function requires that x > 0 and y > 0. It underflows for large arguments.

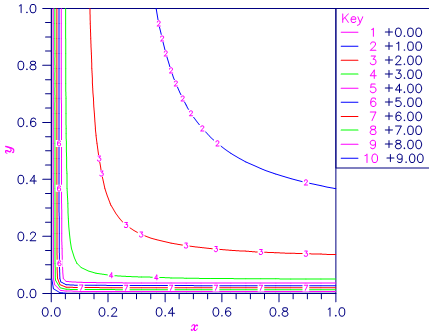
Figure 9.12 — Plot of \(\beta(x,y)\)

Example¶

Evaluate the beta function \(\beta(0.5,0.2)\).

from __future__ import print_function
from numpy import *
from pyimsl.math.beta import beta

x = 0.5
y = 0.2
ans = beta(x, y)
print("beta(%f,%f) = %f" % (x, y, ans))

Output¶

beta(0.500000,0.200000) = 6.268653

Alert Errors¶

IMSL_BETA_UNDERFLOW The arguments must not be so large that the result underflows.

Fatal Errors¶

IMSL_ZERO_ARG_OVERFLOW One of the arguments is so close to zero that the result overflows.