erf

Evaluates the real error function erf(x).

Synopsis

erf (x)

Required Arguments

float x (Input)

Point at which the error function is to be evaluated.

Return Value

The value of the error function erf(x).

Description

The error function erf(x) is defined to be

$$\mathrm{erf}(x) = \frac{2}{(\pi)^{1/2}} \int_0^x e^{-t^2} dt$$

All values of x are legal.

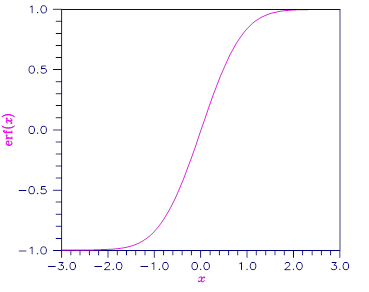
Figure 9.8 — Plot of erf(x)

Example

Evaluate the error function at $x=1/2$.

from __future__ import print_function
from numpy import *
from pyimsl.math.erf import erf

x = 0.5
ans = erf(x)
print("erf(%f) = %f" % (x, ans))

Output

erf(0.500000) = 0.520500