complementaryFCdf

Evaluates the complement of the F distribution function.

Synopsis

complementaryFCdf (f, dfNumerator, dfDenominator)

Required Arguments

float f (Input)

Argument for which Pr(x > f) is to be evaluated.

float dfNumerator (Input)

The numerator degrees of freedom. Argument dfNumerator must be positive.

float dfDenominator (Input)

The denominator degrees of freedom. Argument dfDenominator must be positive.

Return Value

The probability that an F random variable takes a value greater than f.

Description

Function complementaryFCdf evaluates one minus the distribution function of a Snedecor’s F random variable with dfNumerator and dfDenominator. The function is evaluated by making a transformation to a beta random variable, then evaluating the incomplete beta function. If X is an F variate with \(\nu_1\) and \(\nu_2\) degrees of freedom and \(Y=(\nu_1 X)/(\nu_2+\nu_1 X)\), then Y is a beta variate with parameters \(p=\nu_1/2\) and \(q=\nu_2/2\). Function complementaryFCdf also uses a relationship between F random variables that can be expressed as

\[F_F\left(f|\upsilon_1,\upsilon_2\right) = F_F\left(^1\!/_f|\upsilon_2,\upsilon_1\right)\]

where \(F_F\) is the distribution function for an F random variable.

This function provides higher right tail accuracy for the F distribution.

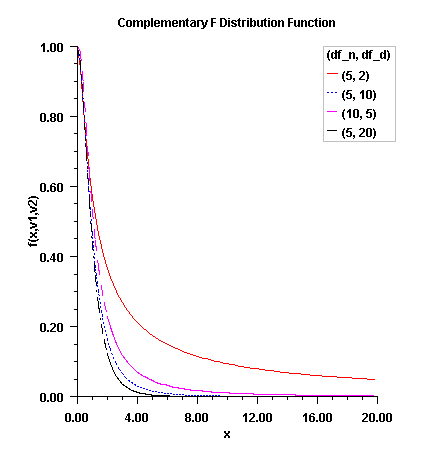
Figure 11.7 — Plot of \(F_F(f/df_n,df_d)\)

Example

This example finds the probability that an F random variable with one numerator and one denominator degree of freedom is greater than 648.

from __future__ import print_function
from numpy import *
from pyimsl.stat.complementaryFCdf import complementaryFCdf

F = 648.0
df_numerator = 1.0
df_denominator = 1.0

p = complementaryFCdf(F, df_numerator, df_denominator)
print("The probability that an F(%2.1f,%2.1f) variate is greater" %
      (df_numerator, df_denominator))
print(" than %5.1f is %6.4f." % (F, p))

Output

The probability that an F(1.0,1.0) variate is greater
 than 648.0 is 0.0250.