complementaryTCdf

Evaluates the complement of the Student’s t distribution.

Synopsis

complementaryTCdf (t, df)

Required Arguments

float t (Input)

Argument for which Pr(x > t) is to be evaluated.

float df (Input)

Degrees of freedom. Argument df must be greater than or equal to 1.0.

Return Value

The probability that a Student’s t random variable takes a value greater than t.

Description

Function complementaryTCdf evaluates one minus the distribution function of a Student’s t random variable with ν = df degrees of freedom. If $t^2\geq\nu$, the following identity relating the complementary Student’s t cumulative distribution function, denoted by $\overline{F} (t|\nu)$, to the incomplete beta ratio function $I_x (a,b)$ is used:

$$\overline{F}(t|\nu) = \frac{1}{2} I_x \left(\frac{\nu}{2},\frac{1}{2}\right), t > 0, t^2 > \nu$$

where

$$x = \frac{v}{t^2+v}$$

and

$$\overline{F}(t|\nu) = 1 - \overline{F}(-t|\nu), t \leq 0, t^2 \geq \nu$$

If $t^2<\nu$, the solution space is partitioned into four algorithms as follows: If $\nu\geq 64$ and $t^2/\nu\leq 0.1$, a Cornish-Fisher expansion is used to evaluate the distribution function. If $\nu<64$ and an integer and $|t|<2.0$, a trigonometric series is used (see Abramowitz and Stegun 1964, Equations 26.7.3 and 26.7.4 with some rearrangement). If $\nu<64$ and an integer and $|t|\geq 2.0$, a series given by Hill (1970) that converges well for large values of t is used. For the remaining $t^2<\nu$ cases, $\overline{F} (t|\nu)$ is calculated using the identity:

$$\overline{F}(t,\nu) = I_{1-x}\left(\frac{\nu}{2},\frac{\nu}{2}\right)$$

where

$$x = \frac{t + \sqrt{t^2 + \nu}}{2 \sqrt{t^2 + \nu}}$$

This function provides higher right tail accuracy for the Student’s t distribution.

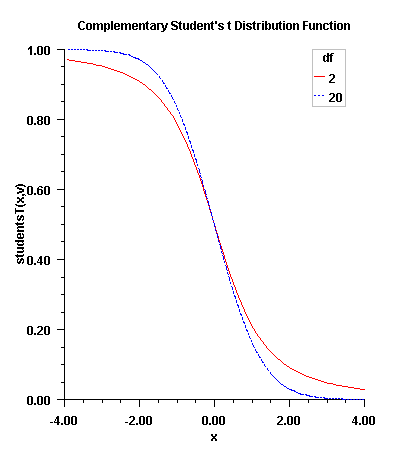
Figure 11.10 — Plot of $F_t(t,df)$

Example

This example finds the 2-tail probability that a Student’s t random variable exceeds 2.447.

from __future__ import print_function
from numpy import *
from pyimsl.stat.complementaryTCdf import complementaryTCdf

t = 2.447
df = 6.0

p = 2.0 * complementaryTCdf(t, df)
print("Pr(|t(%1.0f)| > %4.3f) = %6.4f" % (df, t, p))

Output

Pr(|t(6)| > 2.447) = 0.0500