nonCentralTCdf

Evaluates the noncentral Student’s t distribution function.

Synopsis

nonCentralTCdf(t, df, delta)

Required Arguments

float t (Input)

Argument for which the noncentral Student’s t distribution function is to be evaluated.

int df (Input)

Number of degrees of freedom of the noncentral Student’s t distribution. Argument df must be greater than or equal to 0.0.

float delta (Input)

The noncentrality parameter.

Return Value

The probability that a noncentral Student’s t random variable takes a value less than or equal to t.

Description

Function nonCentralTCdf evaluates the distribution function F of a noncentral t random variable with df degrees of freedom and noncentrality parameter delta; that is, with v = df, δ = delta, and \(t_0\) = t,

\[F(t_0) = \int_{-\infty}^{t_0}{\frac{v^{v/2}e^{-\delta^2/2}}{\sqrt{\pi}\mathit{\Gamma}(v/2)\left(v + x^2\right)^{(v + 1)/2}}} \sum_{i=0}^{\infty}\frac{\mathit{\Gamma}((v + i + 1) / 2)\left[{\delta}x\right]^i\left(2 / \left(v + x^2\right)\right)^{i/2}}{i!}dx\]

where Γ(⋅) is the gamma function. The value of the distribution function at the point \(t_0\) is the probability that the random variable takes a value less than or equal to \(t_0\).

The noncentral t random variable can be defined by the distribution function above, or alternatively and equivalently, as the ratio of a normal random variable and an independent chi-squared random variable. If w has a normal distribution with mean δ and variance equal to one, u has an independent chi-squared distribution with v degrees of freedom, and

\[x = w / \sqrt{u/v}\]

then x has a noncentral t distribution with degrees of freedom and noncentrality parameter δ.

The distribution function of the noncentral t can also be expressed as a double integral involving a normal density function (see, for example, Owen 1962, page 108). The function TNDF uses the method of Owen (1962, 1965), which uses repeated integration by parts on that alternate expression for the distribution function.

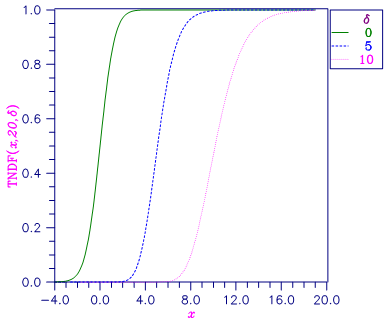
Figure 11.11 — Noncentral Student’s t Distribution Function

Example

Suppose t is a noncentral t random variable with 6 degrees of freedom and noncentrality parameter 6. In this example, we find the probability that t is less than 12.0. (This can be checked using the table on page 111 of Owen 1962, with \(\eta=0.866\), which yields \(\lambda=1.664\).)

from __future__ import print_function
from numpy import *
from pyimsl.stat.nonCentralTCdf import nonCentralTCdf

t = 12.0
df = 6
delta = 6.0
p = nonCentralTCdf(t, df, delta)
print("The probability that t is less than 12 is %6.4f." % p)

Output

The probability that t is less than 12 is 0.9501.