poissonCdf

Evaluates the Poisson distribution function.

Synopsis

poissonCdf (k, theta)

Required Arguments

int k (Input)

Argument for which the Poisson distribution function is to be evaluated.

float theta (Input)

Mean of the Poisson distribution. Argument theta must be positive.

Return Value

The probability that a Poisson random variable takes a value less than or equal to k.

Description

Function poissonCdf evaluates the distribution function of a Poisson random variable with parameter theta. The mean of the Poisson random variable, theta, must be positive. The probability function (with θ = theta) is as follows:

\[f(x|\theta) = e^{-\theta} \theta^x / x!, \phantom{...} \text{for } x = 0,1,2,\ldots\]

The individual terms are calculated from the tails of the distribution to the mode of the distribution and summed. Function poissonCdf uses the recursive relationship

\[f(x+1|\theta) = f(x|\theta)(\theta/(x+1)) \phantom{...} \text{for } x = 0,1,2,\ldots,k-1\]

with \(f(0)=e^{-q}\).

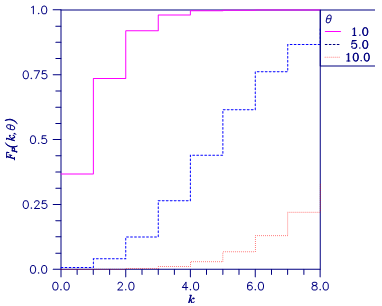
Figure 11.1 — Plot of Fp (k, θ)

Example

Suppose X is a Poisson random variable with \(\theta=10\). In this example, we evaluate the probability that X is less than or equal to 7.

from __future__ import print_function
from numpy import *
from pyimsl.stat.poissonCdf import poissonCdf

k = 7
theta = 10.0
pr = poissonCdf(k, theta)
print("Pr(x <= 7) = %6.4f" % pr)

Output

Pr(x <= 7) = 0.2202

Informational Errors

IMSLS_LESS_THAN_ZERO

Since “k” = # is less than zero, the distribution function is set to zero.