bayesianSeasonalAdj¶

Decomposes a time series into trend, seasonal, and an error component.

Synopsis¶

bayesianSeasonalAdj(w)

Required Arguments¶

float w[] (Input): An array of length nObs containing the stationary time series.

Return Value¶

The average Akaike Bayesian Information Criterion for the estimated model. NaN is returned on error.

Optional Arguments¶

trendOrder, int (Input)

The order of trend differencing where trendOrder ≥ 0.

Default: trendOrder = 2.

seasonalOrder, int (Input)

The order of seasonal differencing where seasonalOrder ≥ 1.

Default: seasonalOrder = 1.

numPredict, int (Input)

The number of values to forecast where numPredict ≥ 0.

Default: numPredict = 0.

span, int (Input)

The number of periods to be processed at one time where 1 ≤ span ≤ nObs/period.

Default: span = nObs/period.

rigidity, float (Input)

Controls the rigidity of the seasonal pattern where 0 ≤ rigidity ≤ 1.0.

Default: rigidity = 1.0.

model, int (Input)

Model option.

`model`	Action
0	Non-additive logistic model
1	Log additive logistic model

Default: model = 0.

printLevel, int (Input)

Printing option.

`printLevel`	Action
0	No printing
1	Prints final results only
2	Prints intermediate and final results

Default: printLevel = 0.

nonseasonalTrend (Output)

An array of length nObs + numPredict containing the estimated trend component for each data value followed by the trend estimates for the numPredict forecasted values.

seasonal (Output)

An array of length nObs + numPredict containing the estimated seasonal components for each data value followed by the estimates for the numPredict forecasted seasonal values.

irregularComponents (Output)

An array of length nObs containing the estimated irregular components.

seriesSmoothed (Output)

An array of length nObs + numPredict containing the estimated smoothed component for each of the time series values followed by the numPredict forecast values.

Description¶

Function bayesianSeasonalAdj is based upon the algorithm published by Akaike (1980). This algorithm uses a Bayesian approach to the problem of fitting the following autoregressive model for a time series \(W_t\) decomposed into a trend and a seasonal component.

Adopting the notation described earlier in the Usage Notes section of this chapter, if

\[t ∈ ℤ = {…, -2, - 1, 0, 1, 2, … }\]

then a seasonal autoregressive model can be represented by the following relationship:

\[W_t = T_t + S_t + A_t\]

where \(W_t\) is the stationary time series with mean μ, \(T_t\) denotes an underlying trend, \(S_t\) denotes a seasonal component and \(A_t\) denotes a noise or irregular component.

A non-Bayesian approach to this problem would be to estimate the trend and seasonal components by minimizing

\[\sum_{t=1}^{N} \left(W_t - T_t - S_t\right)^2 + d^2 \left(\nabla^k T_t + r^2 \nabla_p^l S_t + z^2 \left(\sum_{j=0}^{p-1} S_{t-j}\right)^2\right)\]

where the difference operator is denoted by ∇ and defined as \(\nabla T_t= (T_t-T_{t-1})\), for \(k\geq 1\), \(\nabla^k T_t=\nabla(\nabla^{k-1} T_t)\), with \(\nabla^0 T_t=T_t\). Similarly, \(\nabla_p S_t=(S_t-S_{t-p})\) and \(\nabla^l_p S_t=\nabla_p (\nabla_p^{l-1} S_t)\), \(l\geq 1\), with \(\nabla^0_p S_t =S_t\).

The period of the seasonal component, *p*, the trend order, *k*, and the seasonal order *l* correspond to parameter options trendOrder, and seasonalOrder respectively. *d*, *z*, and *r* are constants determined as follows.

In bayesianSeasonalAdj, the approach is to select the parameter *d*, which controls the smoothness of the trend and seasonality estimates, using Bayesian methods. The prior distribution controls the smoothness of the trend and seasonal components by assuming low-order Gaussian autoregressive models for some differences of these components. The choice of the variance of the Gaussian distribution is realized by maximizing the log likelihood of the Bayesian model.

The other smoothing parameters, *r* and *z*, are determined by the value of rigidity. The default value for rigidity is 1. Larger values of rigidity produce a more rigid seasonal pattern. Normally, a series is first fit using the default value for rigidity. The smoothness of the trend and seasonality estimates are examined and then rigidity is either increased or decreased depending upon whether more or less seasonal smoothing is needed.

Additionally, bayesianSeasonalAdj selects the optimum autoregressive model as the model that minimizes the Akaike Bayesian Information Criterion (ABIC).

\[ABIC = -2 ln(likelihood)\]

where the likelihood in this case is the mixed Bayesian maximum likelihood. Smaller values of ABIC represent a better fit. The basic minimization procedure is applied to blocks of data of length span\*period. The final return value of the criterion is averaged over these blocks. By default, the data is treated in one block.

Example¶

This example uses unadjusted unemployment for women over 20 years of age in the U.S. for 1991-2001, as reported by the U.S. Bureau of Labor Statistics (www.bls.gov).

from __future__ import print_function
from numpy import *
from pyimsl.stat.bayesianSeasonalAdj import bayesianSeasonalAdj
from pyimsl.stat.writeMatrix import writeMatrix

y = array([2968.0, 3009.0, 2962.0, 2774.0, 3040.0, 3165.0,
           3104.0, 3313.0, 3178.0, 3142.0, 3129.0, 3107.0, 3397.0,
           3447.0, 3328.0, 3229.0, 3286.0, 3577.0, 3799.0, 3867.0,
           3655.0, 3360.0, 3310.0, 3369.0, 3643.0, 3419.0, 3108.0,
           3118.0, 3146.0, 3385.0, 3458.0, 3468.0, 3330.0, 3244.0,
           3135.0, 3005.0, 3462.0, 3272.0, 3275.0, 2938.0, 2894.0,
           3106.0, 3150.0, 3289.0, 3136.0, 2829.0, 2776.0, 2467.0,
           2944.0, 2787.0, 2749.0, 2762.0, 2578.0, 2900.0, 3100.0,
           3102.0, 2934.0, 2864.0, 2652.0, 2456.0, 3088.0, 2774.0,
           2701.0, 2555.0, 2677.0, 2741.0, 3052.0, 2966.0, 2772.0,
           2723.0, 2705.0, 2640.0, 2898.0, 2788.0, 2718.0, 2406.0,
           2520.0, 2645.0, 2708.0, 2811.0, 2666.0, 2380.0, 2292.0,
           2187.0, 2750.0, 2595.0, 2554.0, 2213.0, 2218.0, 2449.0,
           2532.0, 2639.0, 2449.0, 2326.0, 2302.0, 2065.0, 2447.0,
           2398.0, 2381.0, 2250.0, 2086.0, 2397.0, 2573.0, 2475.0,
           2299.0, 2054.0, 2127.0, 1935.0, 2425.0, 2245.0, 2298.0,
           2005.0, 2208.0, 2379.0, 2459.0, 2539.0, 2182.0, 1959.0,
           2012.0, 1834.0, 2404.0, 2329.0, 2285.0, 2175.0, 2245.0,
           2492.0, 2636.0, 2892.0, 2784.0, 2771.0, 2878.0, 2856.0])
months = ["Jan", "Feb", "Mar", "Apr", "May", "Jun", "Jul",
          "Aug", "Sep", "Oct", "Nov", "Dec"]
years = ["", "1991", "1992", "1993", "1994", "1995",
         "1996", "1997", "1998", "1999", "2000", "2001", "2002"]
focast = 12
trend = []
seasonal = []
irr_comp = []

abic = bayesianSeasonalAdj(y,
                           trendOrder=2,
                           seasonalOrder=1,
                           numPredict=focast,
                           nonseasonalTrend=trend,
                           seasonal=seasonal,
                           irregularComponents=irr_comp)

print("Average ABIC = %f" % abic)

writeMatrix("TREND with last 12 values forecasted",
            reshape(trend, (12, 12)),
            transpose=True,
            writeFormat="%8.1f",
            rowLabels=months,
            colLabels=years)
writeMatrix("SEASONAL with last 12 values forecasted",
            reshape(seasonal, (12, 12)),
            transpose=True,
            writeFormat="%6.1f",
            rowLabels=months,
            colLabels=years)
writeMatrix("IRREGULAR=Original data-TREND-SEASONAL",
            reshape(irr_comp, (11, 12)),
            transpose=True,
            writeFormat="%6.1f",
            rowLabels=months,
            colLabels=years)

Output¶

 
                  TREND with last 12 values forecasted
         1991      1992      1993      1994      1995      1996      1997
Jan    2879.8    3318.9    3422.6    3228.7    2827.3    2795.7    2743.1
Feb    2918.2    3359.9    3387.8    3206.0    2815.8    2785.6    2720.6
Mar    2955.1    3399.1    3355.5    3177.0    2812.4    2777.9    2694.2
Apr    2990.0    3436.1    3329.5    3142.1    2814.7    2773.2    2665.2
May    3022.7    3469.0    3309.6    3103.9    2819.3    2771.3    2636.0
Jun    3052.8    3496.1    3294.8    3064.8    2825.5    2771.0    2607.4
Jul    3082.8    3514.5    3283.8    3025.7    2830.9    2772.4    2580.8
Aug    3116.2    3521.9    3276.0    2987.3    2833.2    2773.6    2557.2
Sep    3153.4    3517.8    3270.3    2949.0    2831.7    2774.7    2536.3
Oct    3193.8    3503.7    3264.8    2911.3    2826.1    2774.5    2518.0
Nov    3235.6    3482.4    3256.8    2876.6    2816.6    2770.4    2503.0
Dec    3277.6    3455.2    3245.3    2847.6    2805.9    2760.2    2491.5
 
         1998      1999      2000      2001      2002
Jan    2481.3    2352.1    2235.9    2206.0    3166.1
Feb    2469.7    2345.6    2237.6    2239.0    3275.1
Mar    2455.4    2338.1    2239.3    2281.4    3384.1
Apr    2439.0    2328.3    2238.9    2333.1    3493.0
May    2422.8    2315.5    2235.2    2393.9    3602.0
Jun    2408.5    2301.4    2226.3    2464.7    3710.9
Jul    2396.8    2286.0    2212.8    2545.7    3819.9
Aug    2387.7    2269.8    2196.6    2636.7    3928.9
Sep    2380.3    2255.5    2181.3    2735.7    4037.8
Oct    2373.6    2244.6    2171.9    2840.4    4146.8
Nov    2366.6    2238.3    2172.1    2948.2    4255.8
Dec    2359.1    2235.6    2183.3    3057.2    4364.7
 
                  SEASONAL with last 12 values forecasted
       1991    1992    1993    1994    1995    1996    1997    1998    1999
Jan   162.9   165.6   169.3   172.0   173.8   176.3   176.4   177.3   176.4
Feb    51.4    51.5    50.5    49.5    48.6    48.8    50.0    51.1    51.0
Mar   -24.0   -23.9   -23.4   -18.8   -16.3   -13.0    -8.7    -4.9    -3.0
Apr  -191.0  -190.1  -189.1  -188.0  -186.6  -187.8  -188.5  -187.9  -186.6
May  -140.6  -143.3  -145.4  -147.4  -148.1  -147.1  -147.1  -147.9  -147.7
Jun    67.2    66.6    65.8    64.4    63.3    62.2    62.7    63.6    64.9
Jul   176.9   180.1   181.6   183.0   185.5   186.6   185.8   186.1   187.2
Aug   251.9   253.0   252.6   253.3   253.1   252.8   253.7   254.4   255.2
Sep    76.4    77.2    77.1    77.3    75.5    73.3    72.6    70.7    68.9
Oct   -79.5   -80.5   -80.1   -80.8   -81.5   -84.3   -87.6   -90.1   -93.4
Nov  -119.8  -120.7  -120.5  -120.2  -120.4  -119.7  -119.7  -118.1  -117.6
Dec  -235.7  -237.9  -243.0  -247.9  -250.5  -251.2  -254.2  -256.2  -257.5
 
       2000    2001    2002
Jan   177.2   177.6   177.5
Feb    50.8    51.6    51.5
Mar    -1.9    -1.7    -1.8
Apr  -187.2  -186.5  -186.6
May  -145.7  -145.6  -145.7
Jun    65.6    65.1    65.0
Jul   186.4   184.7   184.7
Aug   256.8   256.9   256.9
Sep    67.3    67.0    67.0
Oct   -95.1   -94.6   -94.6
Nov  -117.3  -116.6  -116.6
Dec  -258.1  -257.1  -257.1
 
                  IRREGULAR=Original data-TREND-SEASONAL
       1991    1992    1993    1994    1995    1996    1997    1998    1999
Jan   -74.7   -87.5    51.1    61.2   -57.1   116.0   -21.5    91.4   -81.5
Feb    39.4    35.6   -19.3    16.5   -77.4   -60.4    17.3    74.2     1.5
Mar    30.9   -47.2  -224.1   116.8   -47.1   -63.9    32.5   103.5    45.9
Apr   -25.0   -17.0   -22.5   -16.1   133.9   -30.5   -70.6   -38.0   108.3
May   157.8   -39.7   -18.2   -62.6   -93.1    52.8    31.2   -56.9   -81.9
Jun    45.0    14.3    24.4   -23.1    11.2   -92.1   -25.1   -23.2    30.7
Jul  -155.6   104.4    -7.4   -58.6    83.6    93.0   -58.6   -50.9    99.9
Aug   -55.0    92.1   -60.6    48.4    15.7   -60.4     0.1    -3.1   -49.9
Sep   -51.8    60.0   -17.4   109.6    26.8   -76.0    57.1    -2.1   -25.3
Oct    27.7   -63.3    59.3    -1.5   119.4    32.8   -50.3    42.5   -97.1
Nov    13.2   -51.7    -1.3    19.5   -44.3    54.3   -91.3    5Average ABIC = 1297.640200
3.5     6.3
Dec    65.1   151.7     2.7  -132.8   -99.4   131.0   -50.3   -37.9   -43.1
 
       2000    2001
Jan    11.9    20.4
Feb   -43.5    38.4
Mar    60.5     5.3
Apr   -46.7    28.5
May   118.5    -3.3
Jun    87.1   -37.7
Jul    59.9   -94.4
Aug    85.6    -1.6
Sep   -66.6   -18.7
Oct  -117.8    25.3
Nov   -42.7    46.4
Dec   -91.2    56.0

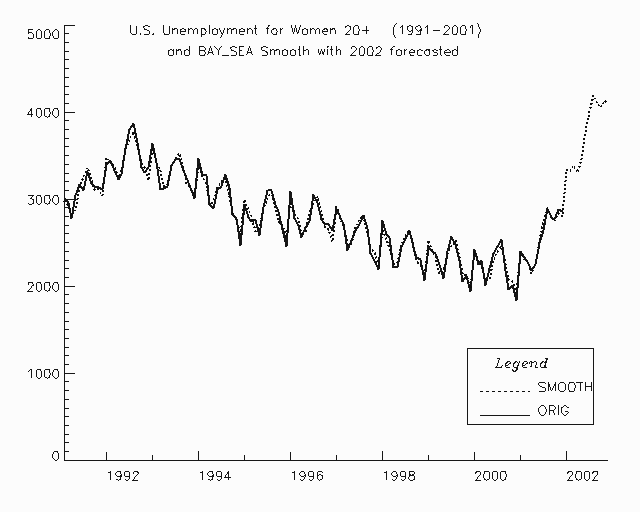
Figure 8.1 — Sample Smoothed Predictions from bayesianSeasonalAdj

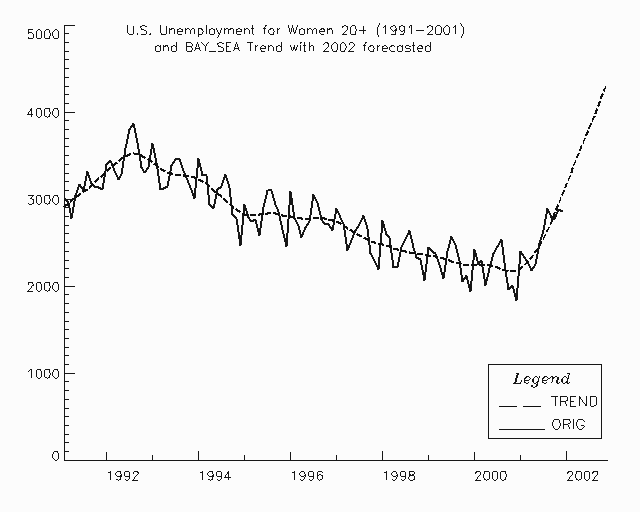
Figure 8.2 — Sample Trend Predictions from bayesianSeasonalAdj