beta¶
Evaluates the complete beta function.
Synopsis¶
beta (a, b)
Required Arguments¶
- float
a(Input) - First beta parameter. It must be positive.
- float
b(Input) - Second beta parameter. It must be positive.
Return Value¶
The value of the beta function β(a, b). If no result can be
computed, then NaN is returned.
Description¶
The beta function, β(a, b), is defined to be
\[\beta(a,b) = \frac{\mathit{\Gamma}(a)\mathit{\Gamma}(b)}{\mathit{\Gamma}(a+b)} =
\int_0^1 t^{a-1} (1-t)^{b-1} dt\]
Example¶
Evaluate the beta function β(0.5, 0.2).
from __future__ import print_function
from pyimsl.stat.beta import beta
x = 0.5
y = 0.2
ans = beta(x, y)
print("beta(%f,%f) = %f\n" % (x, y, ans))
Output¶
beta(0.500000,0.200000) = 6.268653
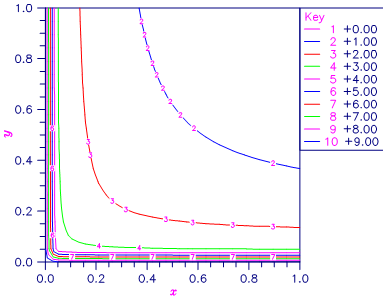
Figure 15.1 — Plot of β (x, b)
The beta function requires that a > 0 and b > 0. It underflows for large arguments.
Alert Errors¶
IMSLS_BETA_UNDERFLOW |
The arguments must not be so large that the result underflows. |
Fatal Errors¶
IMSLS_ZERO_ARG_OVERFLOW |
One of the arguments is so close to zero that the result overflows. |