ga_chromosome
Creates an Imsls_f_chromosome data structure containing unencoded and encoded phenotype information.
Synopsis
#include <imsls.h>
Imsls_f_chromosome *imsls_f_ga_chromosome (..., 0)
The type double function is imsls_d_ga_chromosome.
Return Value
The function imsls_f_ga_chromosome returns an Imsls_f_chromosome data structure, which is required input to imsls_f_ga_individual, imsls_f_ga_population, and imsls_f_ga_random_population. The memory allocated to this data structure can be released using imsls_free.
Synopsis with Optional Arguments
#include <imsls.h>
Imsls_f_chromosome *imsls_f_ga_chromosome (
IMSLS_PRINT,
IMSLS_BINARY, int n_binary,
IMSLS_NOMINAL, int n_nominal, int n_categories[],
IMSLS_INTEGER, int n_integer, int i_intervals[], int i_bounds[],
IMSLS_REAL, int n_real, int r_intervals[], float r_bounds[],
0)
Optional Arguments
IMSLS_PRINT, (Input)
By default, summary results are not printed. This option causes the function to print summary results describing the chromosome structure.
By default, summary results are not printed. This option causes the function to print summary results describing the chromosome structure.
IMSLS_BINARY, int n_binary (Input)
The number of binary phenotypes.
The number of binary phenotypes.
Default: n_binary = 0.
IMSLS_NOMINAL, int n_nominal, int n_categories[] (Input)
The first parameter n_nominal is equal to the number of nominal phenotypes. n_categories is an array of length n_nominal containing the number of nominal categories for each nominal phenotype. Each value of this array must be at least 2 or greater. If partially matched crossover is used during the genetic algorithm search then the array n_categories is ignored since all of its values are assumed equal to n_nominal.
The first parameter n_nominal is equal to the number of nominal phenotypes. n_categories is an array of length n_nominal containing the number of nominal categories for each nominal phenotype. Each value of this array must be at least 2 or greater. If partially matched crossover is used during the genetic algorithm search then the array n_categories is ignored since all of its values are assumed equal to n_nominal.
Default: n_nominal = 0.
IMSLS_INTEGER, int n_integer, int i_intervals[] , int i_bounds[] (Input)
The first parameter n_integer is equal to the number of integer phenotypes. The second parameter in this argument, i_intervals, is a one-dimensional array of length n_integer containing the number of discrete intervals used to map each integer into the chromosome loci. For efficiency, each value in this array should be a power of 2 such as 2, 4, 8, 16, etc. The third parameter, i_bounds is an array of size n_integer by 2 containing the lower and upper bounds for each integer phenotype. The lower and upper bounds for the i-th integer phenotype are equal to i_bounds[2*i] and i_bounds[2 * i+1] respectively. Each integer value submitted to imsls_f_genetic_algorithm for the i-th integer phenotype,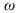
must conform to the inequality:
The first parameter n_integer is equal to the number of integer phenotypes. The second parameter in this argument, i_intervals, is a one-dimensional array of length n_integer containing the number of discrete intervals used to map each integer into the chromosome loci. For efficiency, each value in this array should be a power of 2 such as 2, 4, 8, 16, etc. The third parameter, i_bounds is an array of size n_integer by 2 containing the lower and upper bounds for each integer phenotype. The lower and upper bounds for the i-th integer phenotype are equal to i_bounds[2*i] and i_bounds[2 * i+1] respectively. Each integer value submitted to imsls_f_genetic_algorithm for the i-th integer phenotype,
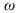must conform to the inequality:Default: n_integer = 0.
IMSLS_REAL, int n_real , int r_intervals[] , float r_bounds[] (Input)
The first parameter n_real is equal to the number of real phenotypes. Point values are mapped into chromosome loci using discretization. The second parameter in this argument, r_intervals, is a one-dimensional array of length n_real containing the number of discrete intervals used to map each real value into the chromosome loci. For efficiency, each value in this array should be a power of 2 such as 2, 4, 8, 16, etc. The third parameter, r_bounds is an array of size n_real by 2 containing the lower and upper bounds for each integer phenotype. The lower and upper bounds for the i-th real phenotype are equal to r_bounds[2*i] and r_bounds[2*i+1] respectively. Hence, r_bounds[2*i+1] must be greater than r_bounds[2*i]. Each real value submitted to imsls_f_genetic_algorithm for the i-th real phenotype,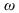
i, must conform to the inequality:
The first parameter n_real is equal to the number of real phenotypes. Point values are mapped into chromosome loci using discretization. The second parameter in this argument, r_intervals, is a one-dimensional array of length n_real containing the number of discrete intervals used to map each real value into the chromosome loci. For efficiency, each value in this array should be a power of 2 such as 2, 4, 8, 16, etc. The third parameter, r_bounds is an array of size n_real by 2 containing the lower and upper bounds for each integer phenotype. The lower and upper bounds for the i-th real phenotype are equal to r_bounds[2*i] and r_bounds[2*i+1] respectively. Hence, r_bounds[2*i+1] must be greater than r_bounds[2*i]. Each real value submitted to imsls_f_genetic_algorithm for the i-th real phenotype,
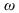i, must conform to the inequality:Default: n_real = 0.
Description
The genetic algorithm requires a chromosome representation of phenotypes. Most textbook applications of genetic algorithms use phenotypes that have a natural binary encoding. Real world problems often have non-binary phenotypes. Phenotypes are parameters used by the fitness function. Those can include any data type. This function allows for easy encoding of binary, nominal, integer and real phenotypes.
Binary phenotypes are mapped directly into the chromosome as binary bits. Each binary phenotype is treated as a single allele. If the user specifies n_binary>0, then the first n_binary bits in the chromosome are allocated for encoding this information. When the fitness function is called during genetic optimization, these bits are translated into zeros and ones and then sent to the fitness function as an integer array of length n_binary.
Nominal phenotypes are mapped into the chromosome following the binary phenotypes. The number of bits assigned to each nominal phenotype is determined from the number of categories for each nominal phenotype. The value n_categories[i] is equal to the number of categories for the i-th nominal phenotype. The number of bits assigned to this category is the smallest value of k such that 2k ≥ n_categories[i], i.e., , where is the ceiling of x (least integer of x). A binary nominal phenotype would be assigned one bit, and one bit would constitute a single allele. A trinary nominal phenotype would be assigned two bits since 22 = 4 ≥ 3, and these bits would be treated as a single allele.
The mapping of multiple bits to a single allele is a key difference between nominal phenotypes and other phenotypes. Alleles for binary, integer and real phenotypes are represented as single bits in the chromosome. The alleles for nominal phenotypes consist of multiple bits. Since crossover occurs between alleles, crossover for nominal phenotypes is treated differently. This ensures that only viable values for nominal phenotypes result from crossover.
It also means that Gray encoding of individual bits has no effect on nominal phenotypes. For many problems Gray encoding is used instead of standard Base-2 encoding to reduce large changes of encoded phenotype values after crossover. As a result, Gray encoding is never applied to nominal phenotypes.
In addition, partially mixed crossover is only an option for nominal phenotypes. Nominal phenotypes combined with partially mixed crossover make it easy to implement search problems similar to the traveling salesman problem.
Both integer and real phenotypes are discretized. Although this is the most common approach to encoding these phenotypes, some problems may benefit from other forms of encoding. If so, users should provide their own encoding, translating the phenotype into a bit representation that can be mapped into binary phenotypes.
Discretization is controlled by two arrays. For integer phenotypes, the array i_intervals contains the number of discrete intervals used to represent each integer. The number of chromosome bits assigned to the i-th integer is determined by the values in this array. If i_intervals[i]= k = 2m then the i-th integer phenotype is assigned m bits. For example, if i_intervals[i]= 4, then this phenotype is assigned two bits.
The array i_bounds contains the upper and lower bounds for each integer phenotype. The lower bound for the i-th integer phenotype is equal to lb = i_bounds[2i], and the upper bound is equal to ub = i_bounds[2i+1]. The values for the i-th phenotype, w, must satisfy the inequality lb ≤ w < ub. w is discretized to w’ using the formula:
Where ⌊x⌋ is the floor of x (greatest integer of x). This results in mapping the i-th integer phenotype, w, into one of the integers 0,1,…, k‑1.
Real phenotypes are handled in the same fashion as integer phenotypes using the values in r_intervals and r_bounds.
The number of chromosome bits assigned to each phenotype are described in the following table:
PHENOTYPE | NUMBER of BITS |
|---|---|
Binary | |
Nominal | |
Integer | |
Real |
See Table 46 for a description of the allele values (bits) for the chromosome. Chromosome bits are ordered first by binary phenotypes in bits 0 through bbits ‑1, then nominals, integers and reals in that order.
The memory allocated to this data structure can be released using imsls_free.
Example
This example creates a chromosome with 1 binary, 2 nominal, 3 integer and 2 real phenotypes. The IMSLS_PRINT argument is used to print a description of the chromosome structure.
#include <imsls.h>
int main(){
int n_binary=1, n_nominal=2, n_integer=3, n_real=2;
/* number of categories for nominal phenotypes */
int n_categories[] = {2, 3};
/* number of intervals and boundaries for integer */
/* phenotypes */
int i_intervals[] = {16, 16, 16};
int i_bounds[] = {0, 1000, -10, 10, -20, 0};
/* number of intervals and boundaries for real */
/* phenotypes */
int r_intervals[] = {512, 1024};
float r_bounds[] = {0.0, 20.0, -20.0, 20.0};
/* Chromosome Data Types */
Imsls_f_chromosome* chromosome;
chromosome = imsls_f_ga_chromosome(
IMSLS_BINARY, n_binary,
IMSLS_NOMINAL, n_nominal, n_categories,
IMSLS_INTEGER, n_integer, i_intervals, i_bounds,
IMSLS_REAL, n_real, r_intervals, r_bounds,
IMSLS_PRINT, 0);
imsls_free(chromosome);
}
Output
The IMSLS_PRINT option produced the following description of the chromosome. The data structure uses 304 bytes. The chromosome has 34 alleles. The first bit is used to represent the binary phenotype.
The next two alleles are assigned to the nominal phenotypes. The first phenotype will be encoded in allele 1 with the integers zero and one since it has only two categories. The second nominal phenotype has 3 categories. It will be encoded with the integers zero, one, and two.
The integer phenotypes are each assigned 4 binary bits. Since the number of intervals is the same for each integer, 16, 4 bits will be used to encode the integers 0-15. If Base-2 encoding is used, the 16th interval will be encoded as 15 = {1111}.
The first real phenotype uses 512 intervals to discretize its value. This is encoded using 9 alleles. The second real phenotype uses 1024 intervals to discretize its value. This requires 10 alleles to properly represent the values 0 to 1023.
*******************************
**** CHROMOSOME STRUCTURE *****
Data Structure length: 304 Bytes
Chromosome length: 34 Bits
******ALLELE ASSIGNMENTS*******
Binary: 0 - 0 n_binary = 1
Nominal: 1 - 2 n_nominal= 2
Integer: 3 - 14 n_integer= 3
Real: 15 - 33 n_real = 2
*******************************
NOMINAL CATEGORIES*************
Variable 0: 2 categories
Variable 1: 3 categories
*******************************
INTEGER BOUNDS*****************
Variable 0: [ 0, 1000]
Variable 1: [ -10, 10]
Variable 2: [ -20, 0]
*******************************
INTEGER BITS*******************
Variable 0: 4 bits
Variable 1: 4 bits
Variable 2: 4 bits
*******************************
INTEGER DISCRETE INTERVALS*****
Variable 0: 16 intervals
Variable 1: 16 intervals
Variable 2: 16 intervals
*******************************
REAL BOUNDS********************
Variable 0: [0,20]
Variable 1: [-20,20]
*******************************
REAL BITS**********************
Variable 0: 9 bits
Variable 1: 10 bits
*******************************
REAL DISCRETE INTERVALS********
Variable 0: 512 intervals
Variable 1: 1024 intervals
*******************************
