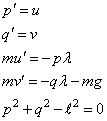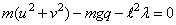dea_petzold

Chapter 5: Differential Equations

dea_petzold_gear

Solves a first order differential -algebraic system of equations, g(t, y, y¢) = 0, using the Petzold-Gear BDF method.

Synopsis

#include <imsl.h>

void imsl_f_dea_petzold_gear_mgr (int task, void **state, …,0)

int imsl_f_dea_petzold_gear (int neq, float *t, float tend, float y[],
float yprime[], void *state, int gcn(), …,0)

The type double functions are imsl_d_dea_petzold_gear_mgr and imsl_d_dea_petzold_gear.

The function imsl_f_dea_petzold_gear_mgr is used to initialize and reset the problem, and the function imsl_f_dea_petzold_gear is the integrator. The descriptions of both of these functions are provided below.

Required Arguments for imsl_f_dea_petzold_gear_mgr

int task (Input)
This function must be called with task set to IMSL_DEA_INITIALIZE to set up for solving a system and with task equal to IMSL_DEA_RESET to clean up after it has been solved. These values for task are defined in the include file, imsl.h.

void **state (Input/Output)
The current state of the solution is held in a structure pointed to by state. It cannot be directly manipulated.

Required Arguments for imsl_f_dea_petzold_gear

int neq (Input)
The number of equations, g(t, y, y¢) = 0

float *t (Input/Output)
Independent variable. On input, t is the initial independent variable value. On output, t is replaced by tend, unless error conditions arise.

float tend (Input)
Mathematical value of t where the solution is desired.

float y[] (Input/Output)
Array with neq components containing the dependent variable values. This array must contain initial values when the integration starts.

float yprime[] (Input/Output)
Array with neq components containing the derivative values, y¢. This array must contain initial values, but they need not be consistent. This function will solve for consistent values of y¢ to satisfy the equations at the starting point.

void *state (Input/Output)
The current state of the solution is held in a structure pointed to by state. It must be initialized by a call to imsl_f_dea_petzold_gear_mgr. It cannot be directly manipulated.

int gcn (int neq, float t, float *y, float *yprime, float *gval) (Input)
User-supplied function to evaluate g(t, y, y¢) where

float *gval (Output)
Array with neq components containing the function values g(t, y, y¢).

gcn returns an int value representing a panic flag.
After an evaluation of g, this panic flag is checked. The value of g is used if the flag is 0. If it has the value -1, the function reduces the step size and possibly the order of the BDF. If the value is -2, the function returns control to the user immediately.

Return Value

Returns a flag that reports what the function did.

Value	Explanation
0	Normal return.
1	A step was taken in the intermediate output mode. The value tend has not been reached.
2	The integration to exactly t_barrier was completed.
3	The integration to t_barrier was completed by stepping past t_barrier and interpolating to evaluate y and y¢.
-1	Too many steps taken.
-2	Error tolerances are too small.
-3	A pure relative error tolerance can't be satisfied.
-6	There were repeated error test failures on the last step.
-7	The BDF corrector equation solver did not converge.
-8	The matrix of partial derivatives is singular.
-10	The BDF corrector equation solver did not converge because the evaluation failure flag was raised.
-11	The evaluation failure flag was raised to quit.
-12	The iteration for the initial value of y¢ did not converge.
-33	There is a fatal error, perhaps caused by invalid input.

Synopsis with Optional Arguments for imsl_f_dea_petzold_gear_mgr

#include <imsl.h>

void imsl_f_dea_petzold_gear_mgr (int task, void **state,

IMSL_INITIAL_STEPSIZE, float intitial_stepsize,

IMSL_T_BARRIER, float t_barrier,

IMSL_MAX_BDF_ORDER, int max_bdf_order,

IMSL_INITIAL_VALUES_INCONSISTENT,

IMSL_JACOBIAN, void jgcn(),

IMSL_JACOBIAN_W_DATA, void jgcn(), void *data,

IMSL_GCN_W_DATA, int gcn(), void *data,

IMSL_NORM_FCN, float norm_fcn(),

IMSL_NORM_FCN_W_DATA, float norm_fcn(),void *data,

IMSL_USER_JAC_FACTOR_SOLVE, void jgcn(), int fac(),
void sol(),

IMSL_USER_JAC_FACTOR_SOLVE_W_DATA, void jgcn(),
int fac(), void sol(), void *data,

Optional Arguments

IMSL_INITIAL_STEPSIZE, float initial_stepsize (Input)
The initial stepsize.
Default: Computed internally.

IMSL_T_BARRIER, float t_barrier (Input)
This optional argument controls whether the code should integrate past a special point, t_barrier, and then interpolate to get y and y¢ at tend. If this optional argument is not present, this is permitted. If this optional argument is present, the code assumes the equations either change on the alternate sides of t_barrier or they are undefined there. In this case, the code creeps up to t_barrier in the direction of integration.

IMSL_MAX_BDF_ORDER, int max_bdf_order (Input)
Maximum order of the Backward Difference Formula (BDF) to be used.
Default: 5

IMSL_INITIAL_VALUES_INCONSISTENT, (Input)
This optional argument controls whether the initial values (t, y, y¢) are consistent. If this optional argument is not supplied, g(t, y, y¢) = 0 at the initial point, otherwise the function will try to solve for y¢ to satisfy this equation.

IMSL_JACOBIAN, void jgcn(int neq, float t, float y[], float yprime[],
float cj, float *pdg) (Input)
User-supplied function to compute the partial derivatives of g(t, y, y¢) where cj is the value cj used in computing the step size and BDF, and pdg is an array of size neq by neq containing the partial derivatives
A = [¶g/¶y + cj¶g/¶y¢]. Each nonzero derivative entry aij is computed and returned in the array location pdg[i*neq+j]. The array contents are zero when jgcn is called. Thus, only the nonzero derivatives have to be defined in jgcn.
Default: Partial derivatives are computed using divided differences.

IMSL_JACOBIAN_W_DATA, void jgcn(int neq, float t, float y[], float yprime[], float cj, float *pdg, void *data), void *data (Input)
User-supplied function to compute the partial derivatives of g(t, y, y¢) which also accepts a pointer to data that is supplied by the user. data is a pointer to the data to be passed to the user-supplied function. See the Introduction, Passing Data to User-Supplied Functions at the beginning of this manual for more details.

IMSL_GCN_W_DATA, int gcn(int neq, float t, float *y, float *yprime,
float *gval, void *data), void *data (Input)
User-supplied function to evaluate g(t, y, y¢). data is a pointer to the data to be passed to the user-supplied function. See the Introduction, Passing Data to User-Supplied Functions at the beginning of this manual for more details.

IMSL_NORM_FCN, float norm_fcn(int neq, float v[], float wt[]) (Input)
User-supplied function to measure the size of the estimated error in each step. Default: The RMS weighted norm given by:

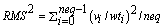
IMSL_NORM_FCN_W_DATA, float norm_fcn(int neq, float v[], float wt[],
void *data), void *data (Input)
User-supplied function to measure the size of the estimated error in each step. data is a pointer to the data to be passed to the user-supplied function. See the Introduction, Passing Data to User-Supplied Functions at the beginning of this manual for more details.

IMSL_USER_JAC_FACTOR_SOLVE, void jgcn(int neq, float t, float y[],
float yprime[], float cj), int fac(), void sol(int neq, float *g, float *y) (Input)
User-supplied functions to compute the partial derivatives
A = [¶g/¶y + cj¶g/¶y¢], factor A, and solve the system ADy = Dg. Using this optional argument allows for handing the factorization and solution steps in a problem specific manner. If successful fac should return 0, if unsuccessful, fac should return a non-zero value. See Example 5 for sample usage of this optional argument.

IMSL_USER_JAC_FACTOR_SOLVE_W_DATA, void jgcn(int neq, float t, float y[], float yprime[], float cj, void *data), int fac(void *data), void sol(int neq, float *g, float *y, void *data), void *data (Input)
User-supplied functions to compute the partial derivatives
A = [¶g/¶y + cj¶g/¶y¢], factor A, and solve the system ADy = Dg. The argument called data is a pointer to the data that is passed to the user-supplied function. See Example 5 for sample usage of this optional argument.

Synopsis with Optional Arguments for imsl_f_dea_petzold_gear

#include <imsl.h>

int imsl_f_dea_petzold_gear (int neq, float *t, float tend, float y[], float yprime[], void **state, int gcn(),

IMSL_ATOL_RTOL_ARRAYS, float *atol, float *rtol,

IMSL_ATOL_RTOL_SCALARS, float atol, float rtol,

IMSL_MAX_NUMBER_STEPS,int max_steps,

IMSL_MAX_STEP, float max_stepsize,

IMSL_ALL_NONNEGATIVE,

IMSL_BDF_ORDER_NEXT_STEP, int next_bdf_order,

IMSL_BDF_ORDER_PREVIOUS_STEP, *int prev_bdf_order,

IMSL_NSTEPS_TAKEN, int *nsteps_taken,

IMSL_NFCN, int *nfcn,

IMSL_NFCNJ, int *nfcnj,

IMSL_NERROR_TEST_FAILURES, int *nerror_test_failures,

IMSL_NCONV_TEST_FAILURES, int *nconv_test_failures,

IMSL_CONDITION, float *condition,

Optional Arguments

IMSL_ATOL_RTOL_ARRAYS, float *atol, float *rtol (Input)
Componentwise tolerances are used for the solution. Arguments atol and rtol are pointers to arrays of length neq to be used for the absolute tolerance and relative tolerance, to be applied to each component of the solution, y. See optional argument IMSL_ATOL_RTOL_SCALARS if scalar values of absolute and relative tolerances are to be applied to all components.
Default: All elements of atol and rtol are set to sqrt(imsl_f_machine(4)).

IMSL_ATOL_RTOL_SCALARS, float atol, float rtol (Input)
Scalar values that apply to the error estimates of all components of y.
See optional argument IMSL_ATOL_RTOL_ARRAYS if separate tolerances are to be applied to each component of y.
Default : atol and rtol are sqrt(imsl_f_machine(4)).

IMSL_MAX_NUMBERSTEPS, int max_steps (Input)
The maximum number of steps.
Default: 500

IMSL_MAX_STEP, float max_stepsize (Input)
The maximum step size allowed.
Default: imsl_f_machine(2).

IMSL_ALL_NONNEGATIVE (Input)
This optional argument controls attempts to constrain all components to be nonnegative.
Default: This constraint is not enforced.

IMSL_BDF_ORDER_NEXT_STEP, int next_bdf_order (Input)
The step size to be attempted on the next move.
Default: Computed internally.

IMSL_BDF_ORDER_PREVIOUS_STEP, int *prev_bdf_order, (Output)
Order of the BDF method used on the last step.

IMSL_NSTEPS_TAKEN, int *nsteps_taken (Output)
The number of steps taken so far.

IMSL_NFCN, int *nfcn (Output)
The number of times that g has been evaluated.

IMSL_NFCNJ, int *nfcn (Output)
The number of times that the partial derivative matrix has been evaluated.

IMSL_NERROR_TEST_FAILURES, int *nerror_test_failures (Output)
The total number of error test failures so far.

IMSL_NCONV_TEST_FAILURES, int *nerror_test_failures, (Output)
The total number of convergence test failures so far. This includes singular iteration matrices.

IMSL_CONDITION, float *condition (Output)
The reciprocal of the condition number of the matrix A. This optional argument cannot be used if optional argument IMSL_USER_EVAL_FACTOR_SOLVE is used in the call to imsl_f_petzold_gear_mgr.

Description

Function imsl_f_dea_petzold_gear finds an approximation to the solution of a system of differential-algebraic equations g(t, y, y¢) = 0, with given initial data for y and y¢. imsl_f_dea_petzold_gear uses BDF formulas, appropriate for systems of stiff ODEs, and attempts to keep the global error proportional to a user-specified tolerance. See Brenan et al. (1989). imsl_f_dea_petzold_gear is efficient for stiff differential-algebraic systems of index 1 or index 0. See Brenan et al. (1989) for a definition of index. Users are encouraged to use double precision accuracy on machines with a short float precision accuracy. The examples given below are in float accuracy because of the desire for consistency with the rest of IMSL C Numerical Library examples. Function imsl_f_dea_petzold_gear is based on the code DASSL designed by L. Petzold (1982-1990).

Example 1

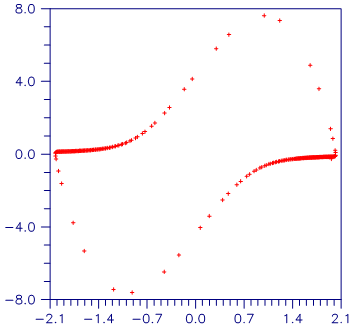
The Van der Pol equation u² + m(u2 - 1) u¢ + u = 0, m > 0, is a single ordinary differential equation with a periodic limit cycle. See Hartman (1964, page 181). For the value m = 5, the equation is integrated from t = 0 until the limit has clearly developed at t = 26. The (arbitrary) initial conditions used here are u(0) = 2 and u¢(0) = - 2/3. Except for these initial conditions and the final t value, this is problem (E2) of the Enright and Pryce (1987) test package. This equation is solved as a differential-algebraic system by defining the first-order system:

Note that the initial condition for the sample program is not consistent, g ¹ 0 at t = 0. The optional argument IMSL_INITIAL_VALUES_INCONSISTENT is used to reflect this.

#include <stdio.h>

#include "imsl.h"

static int gcn(int n, float t, float y[], float ypr[], float gval[]);

#define N 2

void main()

{

int istep, nstep, n = N;

float delt, t, tend, y[N], ypr[N];

char *state;

/* Initialize the solver. */

imsl_f_dea_petzold_gear_mgr(IMSL_DEA_INITIALIZE, &state,

IMSL_INITIAL_VALUES_INCONSISTENT,

0);

t = 0.0;

tend = 26.0;

delt = 0.1;

nstep = (int)(tend/delt)+1;

y[0] = 2.0;

y[1] = -2.0/3.0;

ypr[0] = y[1];

ypr[1] = 0.0;

for (istep = 0; istep < nstep; istep++) {

tend = t+delt;

imsl_f_dea_petzold_gear(n, &t, tend, y, ypr, state, gcn, 0);

}

/* Reset the solver. */

imsl_f_dea_petzold_gear_mgr(IMSL_DEA_RESET, &state, 0);

/* Output results.*/

printf(" T y[0] y[1] y'[0] y'[1]\n");

printf("%10.2f %10.5f %10.5f %10.5f %10.5f\n",

tend, y[0], y[1], ypr[0], ypr[1]);

}

static int gcn(int n, float t, float y[], float ypr[], float gval[])

{

float eps = 0.2;

gval[0] = y[1] - ypr[0];

gval[1] = (1.0-y[0]*y[0])*y[1] - eps*(y[0]+ypr[1]);

return 0;

}

Output

T y[0] y[1] y'[0] y'[1]

26.00 1.46223 -0.24127 -0.24274 -0.09163

Figure 5-1 Van der Pol Cycle, (u(t), u¢(t)), m = 5.

Example 2

The first-order equations of motion of a point-mass m suspended on a massless wire of length 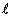under the influence of gravity force, mg and tension value l, in Cartesian coordinates, (p, q), are

This is a genuine differential-algebraic system. The problem, as stated, has an index number equal to the value 3. Thus, it cannot be solved with imsl_f_dea_petzold_gear directly. Unfortunately, the fact that the index is greater than 1 must be deduced indirectly. Typically there will be an error processed which states that the (BDF) corrector equation did not converge. The user then differentiates and replaces the constraint equation. This example is transformed to a problem of index number of value 1 by differentiating the last equation twice. This resulting equation, which replaces the given equation, is the total energy balance:

With initial conditions and systematic definitions of the dependent variables, the system becomes:

The problem is given in English measurement units of feet, pounds, and seconds. The wire has length 6.5 ft, and the mass at the end is 98 lb. Usage of the software does not require it, but standard or “SI” units are used in the numerical model. This conversion of units is done as a first step in the user-supplied evaluation function gcn. A set of initial conditions, corresponding to the pendulum starting in a horizontal position, are provided as output for the input signal of n = 0. The maximum magnitude of the tension parameter, l(t) = y5(t), is computed at the output points, t = 0.1, p, (0.1). This extreme value is converted to English units and printed.

#include <stdio.h>

#include <stdlib.h>

#include <math.h>

#include "imsl.h"

static int gcn(int n, float t, float y[], float ypr[], float gval[]);

#define N 5

void main()

{

int istep, nstep, n = N;

float delt, gval[N], maxlb, maxten, t, tend, tmax, y[N], ypr[N];

char *state;

/* Initialize the solver. */

imsl_f_dea_petzold_gear_mgr(IMSL_DEA_INITIALIZE, &state, 0);

/* Define intitial data. */

t = 0.0;

tend = imsl_f_constant("pi", 0);

delt = 0.1;

nstep = (int)(tend/delt);

/* Get initial conditions. */

gcn(0, t, y, ypr, gval);

maxten = 0;

for (istep =0; istep < nstep; istep++) {

tend = t+delt;

imsl_f_dea_petzold_gear(n, &t, tend, y, ypr, state, gcn, 0);

/* Note max tension value. */

if (fabs(y[4]) > fabs(maxten)) {

tmax = t;

maxten = y[4];

}

/* Reset the solver. */

imsl_f_dea_petzold_gear_mgr(IMSL_DEA_RESET, &state, 0);

printf("max tension = %f at tmax = %f\n", maxten/.4536, tmax);

}

static int gcn(int n, float t, float y[], float ypr[], float gval[])

{

static int first = 1;

static float feetl, grav, lensq, masskg, masslb, meterl, mg;

switch (first) {

case 1:

first = 0;

/* Convert from English to Metric units. */

feetl = 6.5;

masslb = 98.0;

meterl = 1.9812000;

masskg = 44.4520531;

grav = 9.8066502;

mg = masskg*grav;

lensq = meterl*meterl;

* Define initial conditions.

* The pendulum is horizontal with these initial y values.

y[0] = meterl;

y[1] = y[2] = y[3] = y[4] = 0.;

ypr[0] = ypr[1] = ypr[2] = ypr[3] = ypr[4] = 0.;

break;

default:

/* Compute residuals. */

gval[0] = y[2]-ypr[0];

gval[1] = y[3]-ypr[1];

gval[2] = -y[0]*y[4]-masskg*ypr[2];

gval[3] = -y[1]*y[4]-masskg*ypr[3] - mg;

gval[4] = masskg*(y[2]*y[2] + y[3]*y[3]) - mg*y[1] - lensq*y[4];

break;

}

return 0;

}

Output

max tension = 1457.800218 at tmax = 2.500000

Example 3

In this example, we solve a stiff ordinary differential equation (E5) from the test package of Enright and Pryce (1987). The problem is nonlinear with nonreal eigenvalues. It is included as an example because it is a stiff problem, and its partial derivatives are provided in the user supplied function. Providing explicit formulas for partial derivatives is an important consideration for problems where evaluations of the function g(t, y, y¢) are expensive. In addition, an initial integration step-size is given for this test problem. The error tolerance is changed from the defaults to a pure absolute tolerance of 0.1 * sqrt(imsl_f_machine(4)).

#include <stdio.h>

#include <math.h>

#include "imsl.h"

static int gcn(int n, float t, float y[], float ypr[], float gval[]);

static void jgcn(int n, float t, float y[], float ypr[], float cj, float *pdg);

#define N 4

void main()

{

int n = N;

float c0, t, tend, y[N], ypr[N];

char *state;

/* Initialize the solver. */

imsl_f_dea_petzold_gear_mgr(IMSL_DEA_INITIALIZE, &state,

IMSL_INITIAL_STEPSIZE, 5.0e-5,

IMSL_JACOBIAN, jgcn,

0);

/* Define intitial data. */

t = 0.0;

tend = 1000.0;

c0 = 1.76E-3;

y[0] = c0;

y[1] = y[2] = y[3] = 0.;

ypr[0] = ypr[1] = ypr[2] = ypr[3] = 0;

/* Integrate the DEA/ODE. */

imsl_f_dea_petzold_gear(n, &t, tend, y, ypr, state, gcn,

IMSL_ATOL_RTOL_SCALARS, 0.1*sqrt(imsl_f_machine(4)), 0.0,

0);

printf("\nt = %f", t);

imsl_f_write_matrix("Y", 1, 4, y, IMSL_WRITE_FORMAT, "%10.5f", 0);

imsl_f_write_matrix("YPR", 1, 4, ypr, IMSL_WRITE_FORMAT, "%10.5f", 0);

/* Reset the solver. */

imsl_f_dea_petzold_gear_mgr(IMSL_DEA_RESET, &state, 0);

}

static int gcn(int n, float t, float y[], float ypr[], float gval[])

{

float C1, C2, C3, C4;

C1 = 7.89E-10;

C2 = 1.1E7;

C3 = 1.13E9;

C4 = 1.13E3;

gval[0] = -C1*y[0] - C2*y[0]*y[2] - ypr[0];

gval[1] = C1*y[0] - C3*y[1]*y[2] - ypr[1];

gval[2] = C1*y[0] - C2*y[0]*y[2] + C4*y[3] - C3*y[1]*y[2] - ypr[2];

gval[3] = C2*y[0]*y[2] - C4*y[3] - ypr[3];

return 0;

}

static void jgcn(int n, float t, float y[], float ypr[], float cj,

float *pdg)

{

#define PDG(I,J) *(pdg+(I)*(n)+(J))

float C1, C2, C3, C4;

C1 = 7.89E-10;

C2 = 1.1E7;

C3 = 1.13E9;

C4 = 1.13E3;

PDG(0,0) = -C1 - C2*y[2] - cj;

PDG(0,2) = -C2*y[0];

PDG(1,0) = C1;

PDG(1,1) = -C3*y[2] - cj;

PDG(1,2) = -C3*y[1];

PDG(2,0) = C1 - C2*y[2];

PDG(2,1) = -C3*y[2];

PDG(2,2) = -C2*y[0] - C3*y[1] - cj;

PDG(2,3) = C4;

PDG(3,0) = C2*y[2];

PDG(3,2) = C2*y[0];

PDG(3,3) = -C4 - cj;

}

Output

t = 1000.000000

1 2 3 4

0.00162 0.00000 0.00000 0.00000

YPR

1 2 3 4

-0.00000 -0.00000 -0.00000 -0.00000

Example 4

In this example, we compute the solution of n = 10 ordinary differential equations,
g = Hy - y¢, where y(0) = y0 = (1, 1, ¼, 1)T. The value

is evaluated at t = 1. The constant matrix H has entries hi_,j= min(j - i, 0) so it is lower Hessenberg. We use the optional arguments IMSL_FCN_W_DATA and IMSL_JACOBIAN_W_DATA to to pass H to the user-supplied functions for the evaluation of the following intermediate quantities:

1. The function g,

2. The partial derivative matrix A = ¶g/¶y + cj¶g/¶y¢ = H - cjI,

#include <stdio.h>

#include <math.h>

#include "imsl.h"

static int gcn(int n, float t, float y[], float ypr[], float gval[],

void *data);

static void jgcn(int n, float t, float y[], float ypr[], float cj,

float *pdg, void *data);

#define N 10

void main()

{

#define H(I,J) h[(I)*N+(J)]

int n = N, i, j;

float t, tend, y[N], ypr[N], sumy, h[N*N];

char *state;

* Initialize the solver. Use optional arguments to

* allow passing problem specific data to the user

* supplied functions.

imsl_f_dea_petzold_gear_mgr(IMSL_DEA_INITIALIZE, &state,

IMSL_GCN_W_DATA, gcn, h,

IMSL_JACOBIAN_W_DATA, jgcn, h,

0);

t = 0.0;

tend = 1.0;

for (i = 0; i < n; i++) {

y[i] = 1;

ypr[i] = 0;

for (j = 0; j < n; j++) H(i,j) = 0;

}

/* Initialize lower Hessenberg matrix. */

for (i = 0; i < n - 1; i++) {

for (j = 0; j < i + 2; j++) H(i,j) = j-i;

}

for (j = 0; j < n; j++) H(N-1,j) = j-N+1;

* Integrate the DEA/ODE. Note, the function to

* evaluate g() was defined int the call to

* imsl_f_dea_petzold_gear_mgr().

imsl_f_dea_petzold_gear(n, &t, tend, y, ypr, state, NULL, 0);

sumy = 0.0;

for (i = 0; i < N; i++) sumy += y[i];

printf(" T Sum of y[i]\n");

printf(" %15.5f %15.5f\n", tend, sumy);

/* Reset the solver. */

imsl_f_dea_petzold_gear_mgr(IMSL_DEA_RESET, &state, 0);

}

static int gcn(int n, float t, float y[], float ypr[], float gval[],

void *data)

{

int i, j;

float *Hy;

float *h = (float *)data;

/* evaluation of G. */

Hy = imsl_f_mat_mul_rect("A*x",

IMSL_A_MATRIX, n, n, h,

IMSL_X_VECTOR, n, y,

0);

for (i = 0; i < n; i++) gval[i] = Hy[i] - ypr[i];

free(Hy);

return 0;

}

static void jgcn(int n, float t, float y[], float ypr[], float cj,

float *pdg, void *data)

{

#define PDG(I,J) *(pdg+(I)*(n)+(J))

float *h = (float *)data;

int i;

for (i = 0; i < n * n; i++) pdg[i] = h[i];

for (i = 0; i < n; i++) PDG(i,i) -= cj;

}

Output

T Sum of y[i]

1.00000 65.17458

Example 5

In this example, we solve the same problem as in Example 4, but use the optional argument IMSL_EVAL_FACTOR_SOLVE_W_DATA to supply functions to compute the partial derivatives A = [¶g/¶y + cj¶g/¶y¢]¢, factor A, and solve the system ADy = Dg. The optional argument IMSL_EVAL_FACTOR_SOLVE_W_DATA also allows for supplying a pointer to problem-specific data that will be passed to the user-spplied functions when they are called from imsl_f_dea_petzold_gear. The problem specific data in this example is the lower Hessenberg matrix H, and the array A that will contain the partial derivatives A = [¶g/¶y + cj¶g/¶y¢]¢, and factored form of this matrix. Note, in this example, the matrix A containing the partial derivatives and factored form of this matrix is stored local to the example. Using the optional argument IMSL_EVAL_FACTOR_SOLVE_W_DATA allows us to apply problem specific techniques to factor A, and solve the system ADy = Dg.

This example can also serves as a prototype for large, structured (possibly nonlinear) DAE problems where the user must use special methods to store and factor the matrix A and solve the linear system ADy = Dg. The word “factor” is used literally here. A user could, for instance, solve the system using an iterative method. Generally, the factor step can be any preparatory phase required for a later solve step.

#include <stdio.h>

#include <math.h>

#include "imsl.h"

/* Prototypes for local functions. */

static int gcn(int n, float t, float y[], float ypr[], float gval[],

void *h);

static void jgcn(int n, float t, float y[], float ypr[], float cj,

void *data);

static int fac(void *data);

static void sol(int neq, float *wk, float *gval, void *data);

static void srotg (float *sa, float *sb, float *sc, float *ss);

#define N 10

* Define a structure that will be used when passing user-data to

* the user-supplied functions.

typedef struct {

float *a;

float *h;

} problem_data;

#define H(I,J) h[(I)*N+(J)]

#define A(I,J) a[(I)*N+(J)]

void main()

{

int n = N, i, j;

float h[N*N];

float a[N*N];

float t, tend, y[N], ypr[N], sumy;

problem_data data;

char *state;

/* Initialize data. */

t = 0.0;

tend = 1.0;

for (i = 0; i < n; i++) {

y[i] = 1;

ypr[i] = 0;

for (j = 0; j < n; j++) H(i,j) = 0;

/* Initialize lower Hessenberg matrix. */

for (i = 0; i < n - 1; i++) {

for (j = 0; j < i + 2; j++) H(i,j) = j-i;

}

for ( j = 0; j < n; j++) H(N-1,j) = j-N+1;

* Set the pointers to be used in the user-data passed to the

* user-supplied functions. data.a points to the array of partial

* derivatives matrix A, data.h points to the lower Hessenberg matrix H.

data.a = a;

data.h = h;

* Initialize the solver. Use the optional arguments that permit passing

* user-data to the user-supplied functions.

imsl_f_dea_petzold_gear_mgr(IMSL_DEA_INITIALIZE, &state,

IMSL_GCN_W_DATA, gcn, &data,

IMSL_USER_JAC_FACTOR_SOLVE_W_DATA, jgcn, fac,

sol, &data,

0);

* Integrate the DEA/ODE. Note, the function to

* evaluate g() was defined int the call to

* imsl_f_dea_petzold_gear_mgr().

imsl_f_dea_petzold_gear(n, &t, tend, y, ypr, state, NULL, 0);

/* Output results. */

sumy = 0.0;

for (i = 0; i < N; i++) sumy += y[i];

printf(" T Sum of y[i]\n");

printf(" %15.5f %15.5f\n", tend, sumy);

/* Reset the solver. */

imsl_f_dea_petzold_gear_mgr(IMSL_DEA_RESET, &state, 0);

}

* Function to evaluate g(t, y, y').

static int gcn(int n, float t, float y[], float ypr[], float gval[],

void *data)

{

int i, j;

float *h = ((problem_data*)data)->h;

float *Hy;

/* evaluation of G. */

Hy = imsl_f_mat_mul_rect("A*x",

IMSL_A_MATRIX, n, n, h,

IMSL_X_VECTOR, n, y,

0);

for (i = 0; i < n; i++) gval[i] = Hy[i] - ypr[i];

free(Hy);

return 0;

}

* Function to compute partial derivatives.

static void jgcn(int n, float t, float y[], float ypr[], float cj, void *data)

{

int i;

float *a = ((problem_data*)data)->a;

float *h = ((problem_data*)data)->h;

for (i = 0; i< n * n; i++) a[i] = h[i];

for (i = 0; i < n; i++) A(i,i) -= cj;

}

* Function to compute factorization of A.

static int fac( void *data)

{

int i, j, n = N;

float stemp, ss, sc;

float *a = ((problem_data*)data)->a;

float *h = ((problem_data*)data)->h;

for (j = 0; j < n - 1; j++) {

/* Construct Givens transformations. */

srotg(&(A(j,j)), &(A(j,j+1)), &sc, &ss);

/* Apply a Givens transformations. */

for (i = 0; i < n - j - 1; i++) {

stemp = sc * A(j+1+i, 0) + ss * A(j+1+i, j+1);

A(j+1+i, j+1) = sc * A(j+1+i, j+1) - ss * A(j+1+i, 0);

A(j+1+i, 0) = stemp;

}

return 0;

}

* Function to solve Ay = g.

static void sol(int n, float *g, float *y, void *data)

{

int i, j;

float z;

float stemp, ss, sc;

float *a = ((problem_data*)data)->a;

for (j = 0; j < n; j++) y[j] = g[j];

for (j = 0; j < n - 1; j++) {

y[j] = y[j]/A(j,j);

for (i = 0; i < n - j - 1; i++) y[j+1+i] += -y[j]*A(j+1+i,j);

}

y[n-1] = y[n-1]/A(n-1,n-1);

/* Reconstruct Givens rotations. */

for (j = n - 2; j >= 0; j--) {

z = A(j,j+1);

if (fabs(z) < 1.0) {

sc = sqrt(1.0e0 - pow(z, 2));

ss = z;

} else if (fabs(z) > 1.0) {

sc = 1.0/z;

ss = sqrt(1.0e0 - pow(sc, 2));

} else {

sc = 0.0;

ss = 1.0;

}

stemp = sc * y[j] + ss * y[j+1];

y[j+1] = sc * y[j+1] - ss * y[j];

y[j] = stemp;

}

* Local function used during the factorization of A to

* construct a Givens plane rotation.

static void srotg (float *sa, float *sb, float *sc, float *ss)

{

/* Construct a Givens plane rotation */

float r, u, v;

if (fabs (*sa) > fabs (*sb)) {

u = *sa + *sa;

v = *sb / u;

r = sqrt (.25 + v*v) * u;

*sc = *sa / r;

*ss = v * (*sc + *sc);

*sb = *ss;

*sa = r;

} else {

if (*sb != 0.0) {

u = *sb + *sb;

v = *sa / u;

*sa = sqrt (.25 + v*v) * u;

*ss = *sb / *sa;

*sc = v * (*ss + *ss);

if (*sc != 0.0) {

*sb = 1.0 / *sc;

} else {

*sb = 1.0;

}

} else {

*sc = 1.0;

*ss = *sa = *sb = 0.0;

}

return;

}

Visual Numerics, Inc.
Visual Numerics - Developers of IMSL and PV-WAVE
http://www.vni.com/
PHONE: 713.784.3131
FAX:713.781.9260