.p>.CMCH2.DOC!GENEIG_COMPLEX;geneig (complex)
Computes the generalized eigenexpansion of a system Ax = λBx, with A and B complex.
Synopsis
#include <imsl.h>
void imsl_c_geneig (int n, f_complex *a, f_complex *b, f_complex *alpha, float *beta, ..., 0)
The double analogue is imsl_z_geneig.
Required Arguments
int n
(Input)
Number of rows and columns in A and B.
f_complex *a
(Input)
Array of size n × n containing the
coefficient matrix A.
f_complex *b
(Input)
Array of size n × n containing the
coefficient matrix B.
f_complex *alpha
(Output)
Vector of size n containing scalars αi. If βi ≠ 0, λi = αi/βi for
i = 0, …, n − 1 are the eigenvalues of the
system.
f_complex *beta
(Output)
Vector of size n.
Synopsis with Optional Arguments
#include <imsl.h>
void imsl_c_geneig
(int
n,
f_complex
*a,
f_complex
*b,
f_complex
*alpha,
f_complex
*beta
IMSL_VECTORS, f_complex **evec,
IMSL_VECTORS_USER, f_complex evecu[],
IMSL_A_COL_DIM, int a_col_dim,
IMSL_B_COL_DIM, int b_col_dim,
IMSL_EVECU_COL_DIM, int
evecu_col_dim,
0)
Optional Arguments
IMSL_VECTORS, f_complex **evec
(Output)
The address of a pointer to an array of size n × n containing
eigenvectors of the problem. Each vector is normalized to have Euclidean length
equal to the value one. On return, the necessary space is allocated by the
function. Typically, f_complex *evec is declared, and
&evec is
used as an argument.
IMSL_VECTORS_USER, f_complex evecu[]
(Output)
Compute eigenvectors of the matrix. An array of size n × n containing the
matrix of generalized eigenvectors is returned in the space evecu. Each vector
is normalized to have Euclidean length equal to the value one.
IMSL_A_COL_DIM, int a_col_dim
(Input)
The column dimension of
A.
Default: a_col_dim =
IMSL_B_COL_DIM, int b_col_dim
(Input)
The column dimension of
B.
Default: b_col_dim = n.
IMSL_EVECU_COL_DIM, int
evecu_col_dim (Input)
The column dimension of evecu.
Default: evecu_col_dim = n.
Description
The function imsl_c_geneig uses the QZ algorithm to compute the eigenvalues and eigenvectors of the generalized eigensystem Ax = λBx, where A and B are complex matrices of order n. The eigenvalues for this problem can be infinite, so α and β are returned instead of λ. If β is nonzero, λ = α/β.
The first step of the QZ algorithm is to simultaneously reduce A to upper-Hessenberg form and B to upper-triangular form. Then, orthogonal transformations are used to reduce A to quasi-upper-triangular form while keeping B upper triangular. The generalized eigenvalues and eigenvectors for the reduced problem are then computed.
The function imsl_c_geneig is based on the QZ algorithm due to Moler and Stewart (1973).
Examples
Example 1
In this example, the eigenvalue, λ, of system Ax = λBx is solved, where
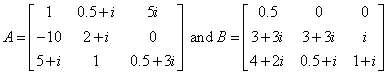
#include <imsl.h>
main()
{
int n = 3;
f_complex alpha[3];
f_complex beta[3];
int i;
f_complex eval[3];
f_complex zero = {0.0, 0.0};
f_complex a[] = {{1.0, 0.0}, {0.5, 1.0}, {0.0, 5.0},
{-10.0, 0.0}, {2.0, 1.0}, {0.0, 0.0},
{5.0, 1.0}, {1.0, 0.0}, {0.5, 3.0}};
f_complex b[] = {{0.5, 0.0}, {0.0, 0.0}, {0.0, 0.0},
{3.0, 3.0}, {3.0, 3.0}, {0.0, 1.0},
{4.0, 2.0}, {0.5, 1.0}, {1.0, 1.0}};
/* Compute eigenvalues */
imsl_c_geneig
(n, a, b, alpha, beta, 0);
for (i=0;
i<n; i++)
if (!imsl_c_eq(beta[i], zero))
eval[i] = imsl_c_div(alpha[i], beta[i]);
else
printf ("Infinite eigenvalue\n");
/* Print eigenvalues */
imsl_c_write_matrix ("Eigenvalues", 1, n, eval, 0);
}
Output
Eigenvalues
1 2 3
( -8.18, -25.38) ( 2.18, 0.61) ( 0.12, -0.39)
Example 2
This example finds the eigenvalues and eigenvectors of the same eigensystem given in the last example.
#include <imsl.h>
main()
{
int n = 3;
f_complex alpha[3];
f_complex beta[3];
int i;
f_complex eval[3];
f_complex *evec;
f_complex zero = {0.0, 0.0};
f_complex a[] = {{1.0, 0.0}, {0.5, 1.0}, {0.0, 5.0},
{-10.0, 0.0}, {2.0, 1.0}, {0.0, 0.0},
{5.0, 1.0}, {1.0, 0.0}, {0.5, 3.0}};
f_complex b[] = {{0.5, 0.0}, {0.0, 0.0}, {0.0, 0.0},
{3.0, 3.0}, {3.0, 3.0}, {0.0, 1.0},
{4.0, 2.0}, {0.5, 1.0}, {1.0, 1.0}};
/* Compute eigenvalues and eigenvectors */
imsl_c_geneig (n, a, b, alpha, beta,
IMSL_VECTORS, & evec,
0);
for (i=0; i<n; i++)
if (!imsl_c_eq(beta[i], zero))
eval[i] = imsl_c_div(alpha[i], beta[i]);
else
printf ("Infinite eigenvalue\n");
/* Print eigenvalues */
imsl_c_write_matrix ("Eigenvalues", 1, n, eval, 0);
/*Print eigenvectors */
imsl_c_write_matrix ("Eigenvectors", n, n, evec, 0);
}
Output
1 2 3
( -8.18, -25.38) ( 2.18, 0.61) ( 0.12, -0.39)
Eigenvectors
1 2 3
1 ( -0.3267, -0.1245) ( -0.3007, -0.2444) ( 0.0371, 0.1518)
2 ( 0.1767, 0.0054) ( 0.8959, 0.0000) ( 0.9577, 0.0000)
3 ( 0.9201, 0.0000) ( -0.2019, 0.0801) ( -0.2215, 0.0968)
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |