Solves a sparse Hermitian positive definite system of linear equations Ax = b. Using optional arguments, any of several related computations can be performed. These extra tasks include returning the symbolic factorization of A, returning the numeric factorization of A, and computing the solution of Ax = b given either the symbolic or numeric factorizations.
Synopsis
#include <imsl.h>
f_complex *imsl_c_lin_sol_posdef_coordinate (int n, int nz, Imsl_c_sparse_elem *a, f_complex *b, ..., 0)
The type d_complex function is imsl_z_lin_sol_posdef_coordinate.
Required Arguments
int n
(Input)
Number of rows in the matrix.
int nz
(Input)
Number of nonzeros in the lower triangle of the matrix.
Imsl_c_sparse_elem *a
(Input)
Vector of length nz containing the
location and value of each nonzero entry in lower triangle of the matrix.
f_complex *b
(Input)
Vector of length n containing the
right-hand side.
Return Value
A pointer to the solution x of the sparse Hermitian positive definite linear system Ax = b. To release this space, use free. If no solution was computed, then NULL is returned.
Synopsis with Optional Arguments
#include <imsl.h>
f_complex
*imsl_c_lin_sol_posdef_coordinate (int n,
int nz,
Imsl_c_sparse_elem *a, f_complex *b,
IMSL_RETURN_SYMBOLIC_FACTOR,
Imsl_symbolic_factor *sym_factor,
IMSL_SUPPLY_SYMBOLIC_FACTOR,
Imsl_symbolic_factor *sym_factor,
IMSL_SYMBOLIC_FACTOR_ONLY,
IMSL_RETURN_NUMERIC_FACTOR,
Imsl_c_numeric_factor *num_factor,
IMSL_SUPPLY_NUMERIC_FACTOR,
Imsl_c_numeric_factor *num_factor,
IMSL_NUMERIC_FACTOR_ONLY,
IMSL_SOLVE_ONLY,
IMSL_MULTIFRONTAL_FACTORIZATION,
IMSL_RETURN_USER, f_complex x[],
IMSL_SMALLEST_DIAGONAL_ELEMENT, float
*small_element,
IMSL_LARGEST_DIAGONAL_ELEMENT, float
*largest_element,
IMSL_NUM_NONZEROS_IN_FACTOR, int
*num_nonzeros,
IMSL_CSC_FORMAT, int *col_ptr, int *row_ind,
float
*values,
0)
Optional Arguments
IMSL_RETURN_SYMBOLIC_FACTOR,
Imsl_symbolic_factor
*sym_factor (Output)
A pointer to a structure of type
Imsl_symbolic_factor containing, on return, the symbolic factorization of
the input matrix.
IMSL_SUPPLY_SYMBOLIC_FACTOR,
Imsl_symbolic_factor
*sym_factor (Input)
A pointer to a structure of type
Imsl_symbolic_factor. This structure contains the symbolic factorization
of the input matrix computed by imsl_c_lin_sol_posdef_coordinate
with the IMSL_RETURN_SYMBOLIC_FACTOR
option.
IMSL_SYMBOLIC_FACTOR_ONLY,
Compute
the symbolic factorization of the input matrix and return. The argument b is ignored.
IMSL_RETURN_NUMERIC_FACTOR,
Imsl_c_numeric_factor
*num_factor (Output)
A pointer to a structure of type
Imsl_c_numeric_factor containing, on return, the numeric factorization of
the input matrix.
IMSL_SUPPLY_NUMERIC_FACTOR,
Imsl_c_numeric_factor
*num_factor (Input)
A pointer to a structure of type
Imsl_c_numeric_factor. This structure contains the numeric factorization
of the input matrix computed by imsl_c_lin_sol_posdef_coordinate
with the IMSL_RETURN_NUMERIC_FACTOR
option.
IMSL_NUMERIC_FACTOR_ONLY,
Compute
the numeric factorization of the input matrix and return. The argument b is ignored.
IMSL_SOLVE_ONLY,
Solve
Ax = b given the numeric or symbolic factorization of A.
This option requires the use of either IMSL_SUPPLY_NUMERIC_FACTOR
or IMSL_SUPPLY_SYMBOLIC_FACTOR.
IMSL_MULTIFRONTAL_FACTORIZATION,
Perform
the numeric factorization using a multifrontal technique. By default a standard
factorization is computed based on a sparse compressed storage scheme.
IMSL_RETURN_USER, f_complex x[]
(Output)
A user-allocated array of length n containing the solution
x.
IMSL_SMALLEST_DIAGONAL_ELEMENT, float
*small_element (Output)
A pointer to a scalar containing
the smallest diagonal element that occurred during the numeric factorization.
This option is valid only if the numeric factorization is computed during this
call to imsl_c_lin_sol_posdef_coordinate.
IMSL_LARGEST_DIAGONAL_ELEMENT, float
*large_element (Output)
A pointer to a scalar containing
the largest diagonal element that occurred during the numeric factorization.
This option is valid only if the numeric factorization is computed during this
call to imsl_c_lin_sol_posdef_coordinate.
IMSL_NUM_NONZEROS_IN_FACTOR, int
*num_nonzeros (Output)
A pointer to a scalar containing
the total number of nonzeros in the factor.
IMSL_CSC_FORMAT, int *col_ptr, int *row_ind, float *values
(Input)
Accept the coefficient matrix in compressed sparse column (CSC)
format.
See the “Introduction” section at the beginnning of this manual for
a discussion of this storage scheme.
Description
The function imsl_c_lin_sol_posdef_coordinate solves a system of linear algebraic equations having a sparse Hermitian positive definite coefficient matrix A. In this function’s default use, a symbolic factorization of a permutation of the coefficient matrix is computed first. Then a numerical factorization is performed. The solution of the linear system is then found using the numeric factor.
The symbolic factorization step of the computation consists of determining a minimum degree ordering and then setting up a sparse data structure for the Cholesky factor, L. This step only requires the “pattern” of the sparse coefficient matrix, i.e., the locations of the nonzeros elements but not any of the elements themselves. Thus, the val field in the Imsl_c_sparse_elem structure is ignored. If an application generates different sparse Hermitian positive definite coefficient matrices that all have the same sparsity pattern, then by using IMSL_RETURN_SYMBOLIC_FACTOR and IMSL_SUPPLY_SYMBOLIC_FACTOR, the symbolic factorization need only be computed once.
Given the sparse data structure for the Cholesky factor L, as supplied by the symbolic factor, the numeric factorization produces the entries in L so that
PAPT = LLT
Here P is the permutation matrix determined by the minimum degree ordering.
The numerical factorization can be carried out in one of two ways. By default, the standard factorization is performed based on a sparse compressed storage scheme. This is fully described in George and Liu (1981). Optionally, a multifrontal technique can be used. The multifrontal method requires more storage but will be faster in certain cases. The multifrontal factorization is based on the routines in Liu (1987). For a detailed description of this method, see Liu (1990), also Duff and Reid (1983, 1984), Ashcraft (1987), Ashcraft et al. (1987), and Liu (1986, 1989).
If an application requires that several linear systems be solved where the coefficient matrix is the same but the right-hand sides change, the options IMSL_RETURN_NUMERIC_FACTOR and IMSL_SUPPLY_NUMERIC_FACTOR can be used to precompute the Cholesky factor. Then the IMSL_SOLVE_ONLY option can be used to efficiently solve all subsequent systems.
Given the numeric factorization, the solution x is obtained by the following calculations:
Ly1 = Pb
Lty2 = y1
x = Pty2
The permutation information, P, is carried in the numeric factor structure.
Examples
Example 1
As a simple example of default use, consider the following Hermitian positive definite matrix
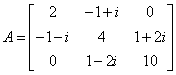
Let xT = (1 + i, 2 + 2i, 3 + 3i) so that Ax = (−2 + 2i, 5 +15i, 36 + 28i)T. The number of nonzeros in the lower triangle is nz = 5.
#include <imsl.h>
main()
{
Imsl_c_sparse_elem a[] = {0, 0, {2.0, 0.0},
1, 1, {4.0, 0.0},
2, 2, {10.0, 0.0},
1, 0, {-1.0, -1.0},
2, 1, {1.0, -2.0}};
f_complex b[] = {{-2.0, 2.0}, {5.0, 15.0}, {36.0, 28.0}};
int n = 3;
int nz = 5;
f_complex *x;
x = imsl_c_lin_sol_posdef_coordinate (n, nz, a, b, 0);
imsl_c_write_matrix ("Solution, x, of Ax = b", n, 1, x, 0);
free (x);
}
Output
Solution, x, of Ax = b
1 ( 1, 1)
2 ( 2, 2)
3 ( 3, 3)
Example 2
Set A = E(2500, 50). Then solve the system Ax = b1 and return the numeric factorization resulting from that call. Then solve the system Ax = b2 using the numeric factorization just computed. Absolute errors and execution time are printed.
#include <imsl.h>
main()
{
Imsl_c_sparse_elem *a;
Imsl_c_numeric_factor numeric_factor;
f_complex b_1[2500];
f_complex b_2[2500];
f_complex *x_1;
f_complex *x_2;
int n;
int ic;
int nz;
int i;
int index;
double time_1;
double time_2;
float *rand_vec;
ic = 50;
n = ic*ic;
index = 0;
/* Generate two right hand sides */
rand_vec =
imsl_f_random_uniform (4*n*sizeof(*rand_vec), 0);
for (i=0; i<n; i++) {
b_1[i].re = rand_vec[index++];
b_1[i].im = rand_vec[index++];
b_2[i].re = rand_vec[index++];
b_2[i].im = rand_vec[index++];
}
/* Build coefficient matrix a */
a =
imsl_c_generate_test_coordinate (n, ic,
&nz,
IMSL_SYMMETRIC_STORAGE,
0);
/* Now solve Ax_1 = b_1 and return the numeric
factorization */
time_1 =
imsl_ctime ();
x_1 = imsl_c_lin_sol_posdef_coordinate (n, nz, a, b_1,
IMSL_RETURN_NUMERIC_FACTOR, &numeric_factor,
0);
time_1 = imsl_ctime () - time_1;
/* Now solve Ax_2 = b_2 given the numeric
factorization */
time_2 =
imsl_ctime ();
x_2 = imsl_c_lin_sol_posdef_coordinate (n, nz, a, b_2,
IMSL_SUPPLY_NUMERIC_FACTOR, &numeric_factor,
IMSL_SOLVE_ONLY,
0);
time_2 = imsl_ctime () - time_2;
printf("time_2/time_1 = %lf\n", time_2/time_1);
}
Output
time_2/time_1 = 0.096386
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |