Solve a nonlinear least-squares problem using a modified Levenberg-Marquardt algorithm.

Synopsis

#include <imsl.h>

float *imsl_f_nonlin_least_squares (void fcn(), int m, int n, ¼, 0)

The type double function is imsl_d_nonlin_least_squares.

Required Arguments

void fcn (int m, int n, float x[], float f[])   (Input/Output)
User-supplied function to evaluate the function that defines the least-squares problem where x is a vector of length n at which point the function is evaluated, and f is a vector of length m containing the function values at point x.

int m   (Input)
Number of functions.

int n   (Input)
Number of variables where n ≤ m.

Return Value

A pointer to the solution x of the nonlinear least-squares problem. To release this space, use free. If no solution can be computed, then NULL is returned.

Synopsis with Optional Arguments

#include <imsl.h>

float *imsl_f_nonlin_least_squares (void fcn(), int m, int n,
IMSL_XGUESS, float xguess[],
IMSL_JACOBIAN, void jacobian(),
IMSL_XSCALE, float xscale[],
IMSL_FSCALE, float fscale[],
IMSL_GRAD_TOL, float grad_tol,
IMSL_STEP_TOL, float step_tol,
IMSL_REL_FCN_TOL, float rfcn_tol,
IMSL_ABS_FCN_TOL, float afcn_tol,
IMSL_MAX_STEP, float max_step,
IMSL_INIT_TRUST_REGION, float trust_region,
IMSL_GOOD_DIGIT, int ndigit,
IMSL_MAX_ITN, int max_itn,
IMSL_MAX_FCN, int max_fcn,
IMSL_MAX_JACOBIAN, int max_jacobian,
IMSL_INTERN_SCALE,
IMSL_TOLERANCE, float tolerance,
IMSL_RETURN_USER, float x[],
IMSL_FVEC, float **fvec,
IMSL_FVEC_USER, float fvec[],
IMSL_FJAC, float **fjac,
IMSL_FJAC_USER, float fjac[],
IMSL_FJAC_COL_DIM, int fjac_col_dim,
IMSL_RANK, int *rank,
IMSL_JTJ_INVERSE, float **jtj_inv,
IMSL_JTJ_INVERSE_USER, float jtj_inv[],
IMSL_JTJ_INV_COL_DIM, int jtj_inv_col_dim,
IMSL_FCN_W_DATA, void fcn(), void *data,
IMSL_JACOBIAN_W_DATA, void jacobian(), void *data,
0)

Optional Arguments

IMSL_XGUESS, float xguess[]   (Input)
Array with n components containing an initial guess.
Default: xguess = 0

IMSL_JACOBIAN, void jacobian (int m, int n, float x[], float fjac[],
int fjac_col_dim)(Input)
User-supplied function to compute the Jacobian where x is a vector of length n at which point the Jacobian is evaluated, fjac is the computed m ´ n Jacobian at the point x, and fjac_col_dim is the column dimension of fjac.
Note that each derivative ¶fi/¶xj should be returned in fjac[(i1)*fjac_col_dim+j-1]

IMSL_XSCALE, float xscale[]   (Input)
Array with n components containing the scaling vector for the variables. xscale is used mainly in scaling the gradient and the distance between two points. See keywords IMSL_GRAD_TOL and IMSL_STEP_TOL for more detail.
Default: xscale[] = 1

IMSL_FSCALE, float fscale[]   (Input)
Array with m components containing the diagonal scaling matrix for the functions. The i-th component of fscale is a positive scalar specifying the reciprocal magnitude of the i-th component function of the problem.
Default: fscale[] = 1

IMSL_GRAD_TOL, float grad_tol   (Input)
Scaled gradient tolerance. The i-th component of the scaled gradient at x is calculated as

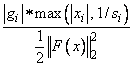
where g = Ñ F(x), s = xscale, and

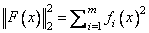
Default:

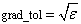
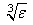 in double where ɛ is the machine precision

IMSL_STEP_TOL, float step_tol   (Input)
Scaled step tolerance. The i-th component of the scaled step between two points x and y is computed as

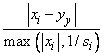
where s = xscale.
Default: step_tol = ɛ2/3 where ɛ is the machine precision.

IMSL_REL_FCN_TOL, float rfcn_tol   (Input)
Relative function tolerance.
Default: rfcn_tol = max (10-10, ɛ2/3), max (10-20, ɛ2/3) in double, where ɛ is the machine precision

IMSL_ABS_FCN_TOL, float afcn_tol   (Input)
Absolute function tolerance.
Default: afcn_tol = max (10-20, ɛ2), max (10-40, ɛ2) in double, where ɛ is the machine precision.

IMSL_MAX_STEP, float max_step   (Input)
Maximum allowable step size.
Default: max_step = 1000 max (ɛ1, ɛ2) where,

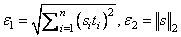
s = xscale, and t = xguess

IMSL_INIT_TRUST_REGION, float trust_region   (Input)
Size of initial trust region radius. The default is based on the initial scaled Cauchy step.

IMSL_GOOD_DIGIT, int ndigit   (Input)
Number of good digits in the function.
Default: machine dependent

IMSL_MAX_ITN, int max_itn   (Input)
Maximum number of iterations.
Default: max_itn = 100

IMSL_MAX_FCN, int max_fcn   (Input)
Maximum number of function evaluations.
Default: max_fcn = 400

IMSL_MAX_JACOBIAN, int max_jacobian   (Input)
Maximum number of Jacobian evaluations.
Default: max_jacobian = 400

IMSL_INTERN_SCALE
Internal variable scaling option. With this option, the values for xscale are set internally.

IMSL_TOLERANCE, float tolerance   (Input)
The tolerance used in determining linear dependence for the computation of the inverse of JTJ. For imsl_f_nonlin_least_squares, if IMSL_JACOBIAN is specified, then tolerance = 100 ´ imsl_d_machine(4) is the default. Otherwise, the square root of imsl_f_machine(4) is the default. For imsl_d_nonlin_least_ squares, if IMSL_JACOBIAN is specified, then tolerance = 100 ´ imsl_machine(4) is the default. Otherwise, the square root of imsl_d_machine(4) is the default.
See imsl_f_machine (Chapter 12, “Utilities”;).

IMSL_RETURN_USER, float x[]   (Output)
Array with n components containing the computed solution.

IMSL_FVEC, float **fvec   (Output)
The address of a pointer to a real array of length m containing the residuals at the approximate solution. On return, the necessary space is allocated by imsl_f_nonlin_least_squares. Typically, float *fvec is declared, and &fvec is used as an argument.

IMSL_FVEC_USER, float fvec[]   (Output)
A user-allocated array of size m containing the residuals at the approximate solution.

IMSL_FJAC, float **fjac   (Output)
The address of a pointer to an array of size m ´ n containing the Jacobian at the approximate solution. On return, the necessary space is allocated by imsl_f_nonlin_least_squares. Typically, float *fjac is declared, and &fjac is used as an argument.

IMSL_FJAC_USER, float fjac[]   (Output)
A user-allocated array of size m ´ n containing the Jacobian at the approximate solution.

IMSL_FJAC_COL_DIM, int fjac_col_dim   (Input)
The column dimension of fjac.
Default: fjac_col_dim = n

IMSL_RANK, int *rank   (Output)
The rank of the Jacobian is returned in *rank.

IMSL_JTJ_INVERSE, float **jtj_inv   (Output)
The address of a pointer to an array of size n ´ n containing the inverse matrix of JTJ  where the J is the final Jacobian. If JTJ is singular, the inverse is a symmetric g2 inverse of JTJ. (See imsl_f_lin_sol_nonnegdef in Chapter 1,
“Linear Systems”  for a discussion of generalized inverses and definition of the
g2 inverse.) On return, the necessary space is allocated by imsl_f_nonlin_least_squares.

IMSL_JTJ_INVERSE_USER, float jtj_inv[]   (Output)
A user-allocated array of size n ´ n containing the inverse matrix of JTJ where the J is the Jacobian at the solution.

IMSL_JTJ_INV_COL_DIM, int jtj_inv_col_dim   (Input)
The column dimension of jtj_inv.
Default: jtj_inv_col_dim = n

IMSL_FCN_W_DATA, void fcn (int m, int n, float x[], float f[], void *data), void *data  (Input)
User supplied function to evaluate the function that defines the least-squares problem, which also accepts a pointer to data that is supplied by the user.  data is a pointer to the data to be passed to the user-supplied function.  See the Introduction, Passing Data to User-Supplied Functions at the beginning of this manual for more details.

IMSL_JACOBIAN_W_DATA, void jacobian (int m, int n, float x[], float fjac[], int fjac_col_dim, void *data), void *data  (Input)
User supplied function to compute the Jacobian, which also accepts a pointer to data that is supplied by the user.  data is a pointer to the data to be passed to the user-supplied function.  See the Introduction, Passing Data to User-Supplied Functions at the beginning of this manual for more details.

Description

The function imsl_f_nonlin_least_squares is based on the MINPACK routine LMDER by Moré et al. (1980). It uses a modified Levenberg-Marquardt method to solve nonlinear least-squares problems. The problem is stated as follows:

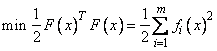
where m ³ n, F : Rn ® Rm, and fi(x) is the i-th component function of F(x). From a current point, the algorithm uses the trust region approach,

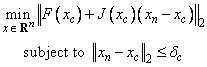
to get a new point xn, which is computed as

xn = xc − (J(xc)T J(xc) + μcI)-1 J(xc)T F(xc)

where μc = 0 if δc ³ ||(J(xc)T J(xc))-1 J(xc)T F(xc)||2 and μc > 0, otherwise. The value
μc is defined by the function. The vector and matrix F(xc) and J(xc) are the function values and the Jacobian evaluated at the current point xc, respectively. This function is repeated until the stopping criteria are satisfied.

The first stopping criterion for imsl_f_nonlin_least_squares occurs when the norm of the function is less than the absolute function tolerance fcn_tol. The second stopping criterion occurs when the norm of the scaled gradient is less than the given gradient tolerance grad_tol. The third stopping criterion for imsl_f_nonlin_least_squares occurs when the scaled distance between the last two steps is less than the step tolerance step_tol. For more details, see Levenberg (1944), Marquardt (1963), or Dennis and Schnabel (1983, Chapter 10).

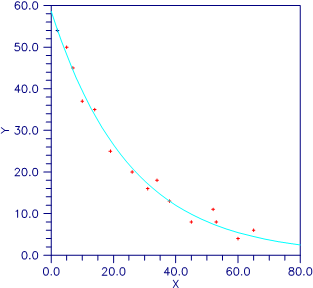
Figure 8-1   Plot of the Nonlinear Fit

Examples

Example 1

In this example, the nonlinear data-fitting problem found in Dennis and Schnabel (1983, p. 225),

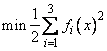
where

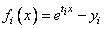
is solved with the data t = (1, 2, 3) and y = (2, 4, 3).

#include <stdio.h>
#include <imsl.h>
#include <math.h>

void            fcn(int, int, float[], float[]);

void main()
{
        int             m=3, n=1;
        float           *result, fx[3];

        result = imsl_f_nonlin_least_squares(fcn, m, n, 0);
        fcn(m, n, result, fx);

/* Print results */

        imsl_f_write_matrix("The solution is", 1, 1, result, 0);
        imsl_f_write_matrix("The function values are", 1, 3, fx, 0);
}                                /* End of main */


void fcn(int m, int n, float x[], float f[])
{
     int   i;
     float y[3] = {2.0, 4.0, 3.0};
     float t[3] = {1.0, 2.0, 3.0};

     for (i=0; i<m; i++)
          f[i] =  exp(x[0]*t[i]) - y[i];

}                                /* End of function */

Output

 The solution is
      0.4401
 
      The function values are
         1           2           3
    -0.447      -1.589       0.744

Example 2

In this example, imsl_f_nonlin_least_squares is first invoked to fit the following nonlinear regression model discussed by Neter et al. (1983, pp. 475−478):

where the ei’s are independently distributed each normal with mean zero and variance σ2. The estimate of σ2 is then computed as

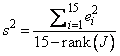
where ei is the i-th residual and J is the Jacobian. The estimated asymptotic variance-covariance matrix of 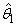 and 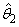 is computed as

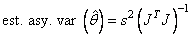2

Finally, the diagonal elements of this matrix are used together with imsl_f_t_inverse_cdf (see Chapter 9, Special Functions) to compute 95% confidence intervals on θ1 and θ2.

 

#include <math.h>
#include <imsl.h>

void            exampl(int, int, float[], float[]);

void main()
{
        int             i, j, m=15, n=2, rank;
        float           a, *result, e[15], jtj_inv[4], s2, dfe;
        char            *fmt="%12.5e";
        static float    xguess[2] = {60.0, -0.03}; 
        static float    grad_tol = 1.0e-3;


        result = imsl_f_nonlin_least_squares(exampl, m, n,
                                         IMSL_XGUESS, xguess,
                                         IMSL_GRAD_TOL, grad_tol,
                                         IMSL_FVEC_USER, e,
                                         IMSL_RANK, &rank,
                                         IMSL_JTJ_INVERSE_USER, jtj_inv,
                                         0);
        dfe = (float) (m - rank);
        s2  = 0.0;
        for (i=0; i<m; i++)
            s2 += e[i] * e[i];
        s2 = s2 / dfe;
        j = n * n;
        for (i=0; i<j; i++)
             jtj_inv[i] = s2 * jtj_inv[i];
                                  /* Print results */

        imsl_f_write_matrix (
                    "Estimated Asymptotic Variance-Covariance Matrix",
                    2, 2, jtj_inv, IMSL_WRITE_FORMAT, fmt, 0);
        printf(" \n           95%% Confidence Intervals   \n    ");
        printf("   Estimate  Lower Limit  Upper Limit \n ");
        for (i=0; i<n; i++) {
            j = i * (n+1);
            a = imsl_f_t_inverse_cdf (0.975, dfe) * sqrt(jtj_inv[j]);
            printf("  %10.3f %12.3f %12.3f \n", result[i],
                    result[i] - a, result[i] + a);
      }
}                                /* End of main */


void exampl(int m, int n, float x[], float f[])
{
     int   i;
     float y[15]     = { 54.0, 50.0, 45.0, 37.0, 35.0, 25.0, 20.0, 16.0,
                         18.0, 13.0,  8.0, 11.0,  8.0,  4.0,  6.0 };
     float xdata[15] = {  2.0,  5.0,  7.0, 10.0, 14.0, 19.0, 26.0, 31.0,
                         34.0, 38.0, 45.0, 52.0, 53.0, 60.0, 65.0 };


     for (i=0; i<m; i++)
          f[i] = y[i] - x[0]*exp(x[1]*xdata[i]);

}                                /* End of function */

Output

Estimated Asymptotic Variance-Covariance Matrix
                       1             2
         1   2.17524e+00  -1.80141e-03
         2  -1.80141e-03   2.97216e-06
 
          95% Confidence Intervals  
      Estimate  Lower Limit  Upper Limit
       58.608       55.422       61.795
       -0.040       -0.043       -0.036

Informational Errors

IMSL_STEP_TOLERANCE                            Scaled step tolerance satisfied. The current point may be an approximate local solution, but it is also possible that the algorithm is making very slow progress and is not near a solution, or that step_tol is too big.

Warning Errors

IMSL_LITTLE_FCN_CHANGE                     Both the actual and predicted relative reductions in the function are less than or equal to the relative function tolerance.

IMSL_TOO_MANY_ITN                                Maximum number of iterations exceeded.

IMSL_TOO_MANY_FCN_EVAL                     Maximum number of function evaluations exceeded.

IMSL_TOO_MANY_JACOBIAN_EVAL         Maximum number of Jacobian evaluations exceeded.

IMSL_UNBOUNDED                                       Five consecutive steps have been taken with the maximum step length.

Fatal Errors

IMSL_FALSE_CONVERGE                            The iterates appear to be converging to a noncritical point.

Visual Numerics, Inc. Visual Numerics - Developers of IMSL and PV-WAVE http://www.vni.com/ PHONE: 713.784.3131 FAX:713.781.9260