.p>.CMCH3.DOC!RADIAL_SCATTERED_FIT;radial_scattered_fit
Computes an approximation to scattered data in Rn for n ³ 1 using radial-basis functions.
Synopsis
#include <imsl.h>
Imsl_f_radial_basis_fit
*imsl_f_radial_scattered_fit (int dimension,
int
num_points,
float
abscissae[], float
fdata[],
int num_centers, ¼, 0)
The type Imsl_d_radial_basis_fit function is imsl_d_radial_scattered_fit.
Required Arguments
int dimension
(Input)
Number of dimensions.
int
num_points (Input)
The number of data points.
float
abscissae[] (Input)
Array of size dimension ´ num_points containing
the abscissae of the data points. The argument abscissae[i][j] is the abscissa
value of the (i+1)-th data point in
the (j+1)-th
dimension.
float fdata[]
(Input)
Array with num_points components
containing the ordinates for the problem.
int
num_centers (Input)
The number of centers to be used when
computing the radial-basis fit. The argument num_centers should be
less than or equal to num_points.
Return Value
A pointer to the structure that represents the radial-basis fit. If a fit cannot be computed, then NULL is returned. To release this space, use free.
Synopsis with Optional Arguments
#include <imsl.h>
Imsl_f_radial_basis_fit
*imsl_f_radial_scattered_fit (int dimension, int num_points,
float abscissae[], float fdata[],
int
num_centers,
IMSL_CENTERS, float centers[],
IMSL_CENTERS_RATIO,
float ratio,
IMSL_RANDOM_SEED, int seed,
IMSL_SUPPLY_BASIS,
float radial_function(),
IMSL_SUPPLY_BASIS_W_DATA, float
radial_function(), void *data,
IMSL_SUPPLY_DELTA, float
delta,
IMSL_WEIGHTS, float weights[],
IMSL_NO_SVD,
0)
Optional Arguments
IMSL_CENTERS
(Input)
User-supplied centers. See the “Description” section of this function
for details.
IMSL_CENTERS_RATIO, float ratio
(Input)
The desired ratio of centers placed on an evenly spaced grid to the
total number of centers. The condition that the same number of centers placed on
a grid for each dimension must be equal. Thus, the actual number of centers
placed on a grid is usually less than ratio*num_centers, but
will never be more than ratio*num_centers. The
remaining centers are randomly chosen from the set of abscissae given in abscissae.
Default:
ratio = 0.5
IMSL_RANDOM_SEED, int seed
The value of
the random seed used when determining the random subset of abscissae to use as
centers. By changing the value of seed on different calls to imsl_f_radial_scattered_fit,
with the same data set, a different set of random centers will be chosen.
Setting seed to
zero forces the random number seed to be based on the system clock, so a
possibly different set of centers will be chosen each time the program is
executed.
Default: seed = 234579
IMSL_SUPPLY_BASIS, float radial_function
(float
distance) (Input)
User-supplied function to compute the
values of the radial functions.
Default: Hardy multiquadric
IMSL_SUPPLY_BASIS_W_DATA, float radial_function
(float
distance, void *data),
void
*data (Input)
User-supplied function to compute the values
of the radial functions, which also accepts a pointer to data that is supplied
by the user. data is a pointer to
the data to be passed to the user-supplied function. See the “Introduction, Passing Data to
User-Supplied Functions” at the beginning of this manual for more
details.
Default: Hardy multiquadric
IMSL_SUPPLY_DELTA, float delta
(Input)
The delta used in the default basis function
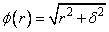
Default: delta = 1
IMSL_WEIGHTS, float weights[]
This
option requires the user to provide the weights.
Default: all weights equal
one
IMSL_NO_SVD
This
option forces the use of a QR decomposition instead of a singular value
decomposition. This may result in space savings for large problems.
Description
The function imsl_f_radial_scattered_fit computed a least-squares fit to scattered data in Rd where d = dimension. More precisely, let n = ndata, x = abscissae, f = fdata, and d = dimension. Then we have
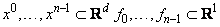
This function computes a function F which approximates the above data in the sense that it minimizes the sum-of-squares error
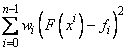
where w = weights. Of course, we must restrict the functional form of F. This is done as follows:
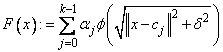
The function ɸ is called the radial function. It maps R1 into R1, only defined for the nonnegative reals. For the purpose of this routine, the user-supplied function
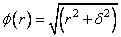
Note that the value of delta is defaulted to 1. It can be set by the user by using the keyword IMSL_DELTA. The parameter δ is used to scale the problem. Generally choose δ to be near the minimum spacing of the centers.
The default basis function is called the Hardy multiquadric, and it is defined as
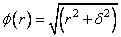
A key feature of this routine is the user’s control over the selection of the basis function.
To obtain the default selection of centers, we first compute the number of centers that will be on a grid and how many are on a random subset of the abscissae. Next, we compute those centers on a grid. Finally, a random subset of abscissa are obtained determining where the centers are placed. Let us examine the selection of centers in more detail.
First, we restrict the computed grid to have the same number of grid values in each of the dimension directions. Then, the number of centers placed on a grid, num_gridded, is computed as follows:
a = (centers_ratio) (num_centers)
b = ëa1/dimensionû
num_gridded = bdimension
Note that there are β grid values in each of the dimension directions. Then we have
num_random = (num_centers) - (num_gridded)
Now we know how many centers will be placed on a grid and how many will be placed on a random subset of the abscissae. The gridded centers are computed such that they are equally spaced in each of the dimension directions. The last problem is to compute a random subset, without replacement, of the abscissa. The selection is based on a random seed. The default seed is 234579. The user can change this using the optional argument IMSL_RANDOM_SEED. Once the subset is computed, we use the abscissae as centers.
Since the selection of good centers for a specific problem is an unsolved problem at this time, we have given the ultimate flexibility to the user. That is, you can select your own centers using the keyword IMSL_CENTERS. As a rule of thumb, the centers should be interspersed with the abscissae.
The return value for this function is a pointer to the structure, which contains all the information necessary to evaluate the fit. This pointer is then passed to the function imsl_f_radial_evaluate to produce values of the fitted function.
Examples
Example 1
This example, generates data from a function and contaminates it with noise on a grid of 10 equally spaced points.The fit is evaluated on a finer grid and compared with the actual function values.
#include <imsl.h>
#include
<math.h>
#define
NDATA 10
#define
NUM_CENTERS 5
#define NOISE_SIZE
0.25
#define F(x)
((float)(sin(2*pi*x)))
main ()
{
int i;
int dim = 1;
float fdata[NDATA];
float *fdata2;
float xdata[NDATA];
float xdata2[2*NDATA];
float pi;
float *noise;
Imsl_f_radial_basis_fit *radial_fit;
pi =
imsl_f_constant ("pi", 0);
imsl_random_seed_set
(234579);
noise = imsl_f_random_uniform(NDATA,
0);
/* Set up the sampled data points with noise.
*/
for (i = 0; i < NDATA; ++i)
{
xdata[i] =
(float)(i)/(float)(NDATA-1);
fdata[i] =
F(xdata[i]) + NOISE_SIZE*(1.0 - 2.0*noise[i]);
}
/*
Compute the radial fit. */
radial_fit =
imsl_f_radial_scattered_fit (dim, NDATA,
xdata,
fdata, NUM_CENTERS, 0);
/* Compare result to the
original function at twice as many values as
there were
original data points. */
for (i = 0; i < 2*NDATA;
++i)
xdata2[i] =
(float)(i/(float)(2*(NDATA-1)));
/* Evaluate the fit at these new points.
*/
fdata2 =
imsl_f_radial_evaluate(2*NDATA, xdata2, radial_fit,
0);
printf("
I TRUE
APPROX ERROR\n");
for (i = 0; i
< 2*NDATA; ++i)
printf("%5d %10.5f %10.5f
%10.5f\n",i+1,F(xdata2[i]), fdata2[i],
F(xdata2[i])-fdata2[i]);
}
Output
I
TRUE APPROX
ERROR
1 0.00000
-0.08980 0.08980
2
0.34202 0.38795
-0.04593
3 0.64279
0.75470 -0.11191
4
0.86603 0.99915
-0.13312
5 0.98481
1.11597 -0.13116
6
0.98481 1.10692
-0.12211
7 0.86603
0.98183 -0.11580
8
0.64279 0.75826
-0.11547
9 0.34202
0.46078 -0.11876
10 -0.00000
0.11996 -0.11996
11 -0.34202
-0.23007 -0.11195
12 -0.64279
-0.55348 -0.08931
13 -0.86603
-0.81624 -0.04979
14 -0.98481
-0.98752 0.00271
15 -0.98481
-1.04276 0.05795
16 -0.86603
-0.96471 0.09868
17 -0.64279
-0.74472 0.10193
18 -0.34202
-0.38203 0.04001
19
0.00000 0.11600 -0.11600
20
0.34202 0.73553 -0.39351
Example 2
This example generates data from a function and contaminates it with noise.We fit this data successively on grids of size 10, 20, ¼, 100. Now interpolate and print the 2-norm of the difference between the interpolated result and actual function values. Note that double precision is used for higher accuracy.
#include <imsl.h>
#include
<stdio.h>
#include <math.h>
#define
NDATA 100
#define
NUM_CENTERS 100
#define
NRANDOM 200
#define
NOISE_SIZE 1.0
#define
G(x,y)
(exp((y)/2.0)*sin(x) - cos((y)/2.0))
double radial_function (double
r);
main()
{
int i;
int ndata;
double *fit;
double ratio;
double fdata[NDATA+1];
double xydata[2 * NDATA+1];
double pi;
double *noise;
int num_centers;
Imsl_d_radial_basis_fit *radial_struct;
pi =
imsl_d_constant ("pi", 0);
/* Get the random numbers
used for the noise. */
imsl_random_seed_set
(234579);
noise = imsl_d_random_uniform (NRANDOM+1,
0);
for (i = 0; i < NRANDOM; ++i) noise[i] = 1.0 - 2.0
* noise[i];
printf("
NDATA || Error ||_2
\n");
for (ndata = 10; ndata <= 100 ; ndata += 10)
{
num_centers =
ndata;
/* Set up the sampled data points with noise.
*/
for (i = 0; i < 2 * ndata; i
+= 2) {
xydata[i] = 3. *
(noise[i]);
xydata[i + 1] = 3. * (noise[i +
1]);
fdata[i / 2] = G(xydata[i], xydata[i +
1])
+ NOISE_SIZE * noise[i];
}
/* Compute the radial fit.
*/
ratio =
0.5;
radial_struct=
imsl_d_radial_scattered_fit (2, ndata,
xydata,
fdata,
num_centers,
IMSL_CENTERS_RATIO,
ratio,
IMSL_SUPPLY_BASIS,
radial_function,
0);
fit = imsl_d_radial_evaluate
(ndata, xydata, radial_struct,
0);
for (i = 0; i < ndata;
++i) fit[i] -= fdata[i];
printf("%8d %17.8f \n", ndata,
imsl_d_vector_norm(ndata, fit, 0));
}
}
double radial_function (double r)
{
return log(1.0+r);
}
Output
NDATA ||
Error ||_2
10 0.00000000
20 0.00000000
30 0.00000000
40 0.00000000
50 0.00000000
60 0.00000000
70 0.00000000
80 0.00000000
90 0.00000000
100 0.00000000
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |