Trains a multilayered feedforward neural network.
Synopsis
#include <imsls.h>
float
*imsls_f_mlff_network_trainer (Imsls_f_NN_Network
*ff_net,
int
n_observations, int
n_categorical, int
n_continuous,
int
categorical[],
float
continuous[], float output[], ..., 0)
The type double function is imsls_d_mlff_network_trainer.
Return Value
An array of length 5 containing the summary statistics from
the network training, organized as follows:
z[0] =
Error sum of squares at the optimum
z[1] =
Total number of Stage I iterations
z[2] =
Smallest error sum of squares after Stage I training
z[3] =
Total number of Stage II iterations
z[4] =
Smallest error sum of squares after Stage II training
If training is unsuccessful, NULL is returned.
Required Arguments
Imsls_f_NN_Network *ff_net
(Input/Output)
Pointer to a structure of type Imsls_f_NN_Network
containing the feedforward network. See imsls_f_mlff_network. On return, the weights and bias
values are updated.
int n_observations
(Input)
Number of network training patterns.
int n_categorical
(Input)
Number of categorical attributes. n_categorical +
n_continuous
must equal n_inputs, where n_inputs is the number
of input attributes in the network. n_inputs =
ff_net->layers[0].n_nodes. For more details, see imsls_f_mlff_network.
int n_continuous
(Input)
Number of continuous attributes. n_categorical + n_continuous must
equal n_inputs, where n_inputs is the number
of input attributes in the network. n_inputs =
ff_net->layers[0].n_nodes. For more details, see imsls_f_mlff_network.
int categorical[]
(Input)
Array of size n_observations by
n_categorical
containing the input training patterns. Each row of categorical contains a
training pattern.
float continuous[]
(Input)
Array of size n_observations
by n_continuous
containing the input training patterns. Each row of continuous contains a
training pattern.
float output[]
(Input)
Array of size n_observations by
n_outputs
containing the output training patterns, where n_outputs is the
number of output perceptrons in the network. n_outputs = ff_net->layers[ff_net->n_layers-1].n_nodes. For more
details, see imsls_f_mlff_network.
Synopsis with Optional Arguments
#include <imsls.h>
float *imsls_f_mlff_network_trainer (Imsls_f_NN_Network
*ff_net,
int n_observations , int n_categorical, int n_continuous,
float categorical[],
int continuous[], float output[],
IMSLS_STAGE_I, int
n_epochs, int epoch_size,
IMSLS_NO_STAGE_II,
IMSLS_MAX_STEP, float max_step,
IMSLS_MAX_ITN, int max_itn,
IMSLS_MAX_FCN, int max_fcn,
IMSLS_REL_FCN_TOL, float rfcn_tol,
IMSLS_GRAD_TOL, float grad_tol,
IMSLS_TOLERANCE, float tolerance,
IMSLS_PRINT,
IMSLS_RESIDUAL, float *residuals,
IMSLS_RESIDUAL_USER, float residuals[],
IMSLS_GRADIENT, float *gradients,
IMSLS_GRADIENT_USER, float gradients[],
IMSLS_FORECASTS, float *forecasts,
IMSLS_FORECASTS_USER, float forecasts[],
IMSLS_WEIGHTS, float *weights,
IMSLS_WEIGHTS_USER, float weights[],
IMSLS_RETURN_USER, float
z[],
0)
Optional Arguments
IMSLS_STAGE_I,
int n_epochs, int
epoch_size
(Input)
Argument
n_epochs is the
number epochs used for Stage I training and argument epoch_size is the
number of observations used during each epoch. If epoch training is
not needed, set epoch_size = n_observations and
n_epochs=1.
Default: n_epochs=15, epoch_size = n_observations.
IMSLS_NO_STAGE_II
(Input)
Specifies no Stage II training is performed.
Default: Stage II training is performed.
IMSLS_MAX_STEP, float max_step
(Input)
Maximum allowable step size in the optimizer.
Default: max_step = 1000
IMSLS_MAX_ITN, int max_itn
(Input)
Maximum number of iterations in the optimizer, per epoch.
Default: max_itn=1000
IMSLS_MAX_FCN,
int max_fcn
(Input)
Maximum number of function evaluations in the optimizer, per
epoch.
Default: max_fcn=400
IMSLS_REL_FCN_TOL, float rfcn_tol
(Input)
Relative function tolerance in the optimizer.
Default: rfcn_tol = max (10−10, ɛ2∕3), max (10−20, ɛ2∕3) in double
IMSLS_GRAD_TOL, float grad_tol
(Input)
Scaled gradient tolerance in the optimizer.
Default:  ,
, 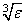 in double where ɛ is the machine
precision.
in double where ɛ is the machine
precision.
IMSLS_TOLERANCE,
float
tolerance (Input)
Absolute accuracy tolerance for the sum
of squared errors in the optimizer.
Default: tolerance = 0.1
IMSLS_PRINT
(Input)
Printing is performed.
Default: No printing is
performed.
IMSLS_RESIDUAL
float **residuals
(Output)
The address of a pointer to an array with n_observations by
n_outputs
containing the residuals for each observation in the training data, where
n_outputs is the
number of output perceptrons in the network.
n_outputs = ff_net->layers[ff_net->n_layers-1].n_nodes.
IMSLS_RESIDUAL_USER
float residuals[]
(Output)
Storage for array residuals is provided
by user. See IMSLS_RESIDUAL.
IMSLS_GRADIENT float
**gradients
(Output)
The address of a pointer gradients to an array
of size
n_links + n_nodes – n_inputs to store the gradients for each weight found at the optimum
training stage, where n_links = ffnet->n_links,
n_nodes = ff_net->n_nodes,
and
n_inputs
= ff_net->layers[0].nodes.
IMSLS_GRADIENT_USER
float gradients[]
(Output)
Storage for array gradients is provided
by user. See IMSLS_GRADIENT.
IMSLS_FORECASTS
float **forecasts
(Output)
The address of a pointer forecasts to an array
of size n_observations by
n_outputs, where
n_outputs is the
number of output perceptrons in the network.
n_outputs = ff_net->layers[ff_net->n_layers-1].n_nodes.
The values of the ith row are the forecasts for the outputs for the
ith training pattern.
IMSLS_FORECASTS_USER
float forecasts[]
(Output)
Storage for array forecasts is provided
by user. See IMSLS_FORECASTS.
IMSLS_RETURN_USER,
float z[]
(Output)
User-supplied array of length 5. Upon completion,
z contains the
return array of training statistics.
Description
Function imsls_f_mlff_network_trainer trains a multilayered feedforward neural network returning the forecasts for the training data, their residuals, the optimum weights and the gradients associated with those weights. Linkages among perceptrons allow for skipped layers, including linkages between inputs and perceptrons. The linkages and activation function for each perceptron, including output perceptrons, can be individually configured. For more details, see optional arguments IMSLS_LINK_ALL, IMSLS_LINK_LAYER, and IMSLS_LINK_NODE in imsls_f_mlff_network.
Training Data
Neural network training patterns consist of the following three types of data:
1. categorical input attributes
2. continuous input attributes
3. continuous output classes
The first data type contains the encoding of any nominal input attributes. If binary encoding is used, this encoding consists of creating columns of zeros and ones for each class value associated with every nominal attribute. If only one attribute is used for input, then the number of columns is equal to the number of classes for that attribute. If more columns appear in the data, then each nominal attribute is associated with several columns, one for each of its classes.
Each column consists of zeros, if that classification is not associated with this case, otherwise, one if that classification is associated. Consider an example with one nominal variable and two classes: male and female (male, male, female, male, female). With binary encoding, the following matrix is sent to the training engine to represent this data:
 .
.
Continuous input and output data are passed to the training engine using two double precision arrays: continuous and outputs. The number of rows in each of these matrices is n_observations. The number of columns in continuous and outputs, corresponds to the number of input and output variables, respectively.
Network Configuration
The network configuration consists of the following:
• the number of inputs and outputs,
• the number of hidden layers,
• a description of the number of perceptrons in each layer,
• and a description of the linkages among the perceptrons.
This description is passed into imsls_f_mlff_network_trainer using the structure Imsls_f_NN_Network. See imsls_f_mlff_network.
Training Efficiency
The training efficiency determines the time it takes to train the network. This is controlled by several factors. One of the most important factors is the initial weights used by the optimization algorithm. These are taken from the initial values provided in the structure Imsls_f_NN_Network, ff_net->links[i].weight. Equally important are the scaling and filtering applied to the training data.
In most cases, all variables, particularly output variables, should be scaled to fall within a narrow range, such as [0, 1]. If variables are unscaled and have widely varied ranges, then numerical overflow conditions can terminate network training before an optimum solution is calculated.
Output
Output from imsls_f_mlff_network_trainer consists of scaled values for the network outputs, a corresponding forecast array for these outputs, a weights array for the trained network, and the training statistics. The Imsls_f_NN_Network structure is updated with the weights and bias values and can be used as input to imsls_f_mlff_network_forecast. For more details about the weights and bias values, see Table 3.
Examples
Example 1
This example trains a two-layer network using 100 training patterns from one nominal and one continuous input attribute. The nominal attribute has three classifications which are encoded using binary encoding. This results in three binary network input columns. The continuous input attribute is scaled to fall in the interval [0,1].
The network training targets were generated using the relationship:
Y = 10*X1 + 20*X2 + 30*X3 + 2.0*X4,
where X1, X2, X3 are the three binary columns, corresponding to the categories 1-3 of the nominal attribute, and X4 is the scaled continuous attribute.
The structure of the network consists of four input nodes and two layers, with three perceptrons in the hidden layer and one in the output layer. The following figure illustrates this structure:
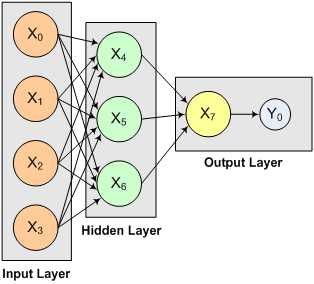
Figure 13- 11: A 2-layer, Feedforward Network with 4 Inputs and 1 Output
There are a total of 15 weights and 4 bias weights in this network. The activation functions are all linear.
Since the target output is a linear function of the input attributes, linear activation functions guarantee that the network forecasts will exactly match their targets. Of course, the same result could have been obtained using multiple regression. Printing is turned on to show progress during the training session.
#include "imsls.h"
#include <stdio.h>
void main()
{
/* A 2D matrix of values for the categorical training
attribute. In this example, the single categorical
attribute has 3 categories that are encoded using binary
encoding for input into the network.
{1,0,0} = category 1
{0,1,0} = category 2
{0,0,1} = category 3
*/
int categorical[300] =
{
1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,
1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,
1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,
1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,
0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,
0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,
0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,
0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,
0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,
0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,
0,0,1,0,0,1,0,0,1,0,0,1,0,0,1
};
/* A matrix of values for the continuous training attribute */
float continuous[100] = {
4.007054658,7.10028447,4.740350984,5.714553211,6.205437459,
2.598930065,8.65089967,5.705787357,2.513348184,2.723795955,
4.1829356,1.93280416,0.332941608,6.745567628,5.593588463,
7.273544478,3.162117939,4.205381208,0.16414745,2.883418275,
0.629342241,1.082223406,8.180324708,8.004894314,7.856215418,
7.797143157,8.350033996,3.778254431,6.964837082,6.13938006,
0.48610387,5.686627923,8.146173848,5.879852653,4.587492779,
0.714028533,7.56324211,8.406012623,4.225261454,6.369220241,
4.432772218,9.52166984,7.935791508,4.557155333,7.976015058,
4.913538616,1.473658514,2.592338905,1.386872932,7.046051685,
1.432128376,1.153580985,5.6561491,3.31163251,4.648324851,
5.042514515,0.657054195,7.958308093,7.557870384,7.901990083,
5.2363088,6.95582150,8.362167045,4.875903563,1.729229471,
4.380370223,8.527875685,2.489198107,3.711472959,4.17692681,
5.844828801,4.825754155,5.642267843,5.339937786,4.440813223,
1.615143829,7.542969339,8.100542684,0.98625265,4.744819569,
8.926039258,8.813441887,7.749383991,6.551841576,8.637046998,
4.560281415,1.386055087,0.778869034,3.883379045,2.364501589,
9.648737525,1.21754765,3.908879368,4.253313879,9.31189696,
3.811953836,5.78471629,3.414486452,9.345413015,1.024053777
};
/* A 2D matrix containing the training outputs for this network.
In this case there is an exact linear relationship between these
outputs and the inputs: output = 10*X1 +20*X2 + 30*X3 +2*X4,
where X1-X3 are the categorical variables and X4 is the continuous
attribute variable. Output is unscaled.
*/
float output[100];
Imsls_f_NN_Network *ffnet;
float *stats;
int n_obs= 100, n_cat=3, n_cont=1;
int i;
float *residuals, *forecasts, *weights;
float bias, coef1, coef2, coef3, coef4;
int hidActFcn[3] = {IMSLS_LINEAR,IMSLS_LINEAR,IMSLS_LINEAR};
/* Scale continuous attribute into the interval [0, 1]
and generate outputs */
for(i=0; i < 100; i++)
{
continuous[i] = continuous[i]/10.0;
output[i] = (10 * categorical[i*3]) + (20 * categorical[i*3+1]) +
(30 * categorical[i*3+2]) + (20 * continuous[i]);
}
/* Create network */
ffnet = imsls_f_mlff_network_init(4,1);
imsls_f_mlff_network(ffnet, IMSLS_CREATE_HIDDEN_LAYER, 3,
IMSLS_ACTIVATION_FCN, 1, &hidActFcn,
IMSLS_LINK_ALL, 0);
/* Set initial weights */
for (i=0; i<ffnet->n_links; i++)
{
/* hidden layer 1 */
if (ffnet->nodes[ffnet->links[i].to_node].layer_id == 1)
ffnet->links[i].weight = .25;
/* output layer */
if (ffnet->nodes[ffnet->links[i].to_node].layer_id == 2)
ffnet->links[i].weight = .33;
}
/* Initialize seed for consisten results */
imsls_random_seed_set(12345);
stats = imsls_f_mlff_network_trainer(ffnet, n_obs, n_cat, n_cont,
categorical,continuous, output,
IMSLS_STAGE_I, 10, 100,
IMSLS_MAX_FCN, 1000,
IMSLS_REL_FCN_TOL, 1.0e-20,
IMSLS_GRAD_TOL, 1.0e-20,
IMSLS_MAX_STEP, 5.0,
IMSLS_TOLERANCE, 1.0e-5,
IMSLS_PRINT,
IMSLS_RESIDUAL, &residuals,
IMSLS_FORECASTS, &forecasts,
0);
printf("Predictions for Last Ten Observations: \n");
for(i=90; i < 100; i++){
printf("observation[%d] %f Prediction %f Residual %f \n", i, output[i],
forecasts[i], residuals[i]);
}
/* hidden layer nodes bias value * link weight */
bias = ffnet->nodes[ffnet->n_nodes-4].bias * ffnet->links[12].weight +
ffnet->nodes[ffnet->n_nodes-3].bias * ffnet->links[13].weight +
ffnet->nodes[ffnet->n_nodes-2].bias * ffnet->links[14].weight;
bias += ffnet->nodes[ffnet->n_nodes-1].bias; /* the bias of the output node */
coef1 = ffnet->links[0].weight * ffnet->links[12].weight;
coef1 += ffnet->links[4].weight * ffnet->links[13].weight;
coef1 += ffnet->links[8].weight * ffnet->links[14].weight;
coef2 = ffnet->links[1].weight * ffnet->links[12].weight;
coef2 += ffnet->links[5].weight * ffnet->links[13].weight;
coef2 += ffnet->links[9].weight * ffnet->links[14].weight;
coef3 = ffnet->links[2].weight * ffnet->links[12].weight;
coef3 += ffnet->links[6].weight * ffnet->links[13].weight;
coef3 += ffnet->links[10].weight * ffnet->links[14].weight;
coef4 = ffnet->links[3].weight * ffnet->links[12].weight;
coef4 += ffnet->links[7].weight * ffnet->links[13].weight;
coef4 += ffnet->links[11].weight * ffnet->links[14].weight;
coef1 += bias;
coef2 += bias;
coef3 += bias;
printf("Bias: %f \n", bias);
printf("X1: %f \n", coef1);
printf("X2: %f \n", coef2);
printf("X3: %f \n", coef3);
printf("X4: %f \n", coef4);
imsls_f_mlff_network_free(ffnet);
}
Output
TRAINING PARAMETERS:
Stage II Opt. = 1
n_epochs = 10
epoch_size = 100
max_itn = 1000
max_fcn = 1000
max_step = 5.000000
rfcn_tol = 1e-20
grad_tol = 1e-20
tolerance = 0.000010
STAGE I TRAINING STARTING
Stage I: Epoch 1 - Epoch Error SS = 3.57886e-10 (Iterations=34)
Stage I Training Converged at Epoch = 1
STAGE I FINAL ERROR SS = 0.000000
OPTIMUM WEIGHTS AFTER STAGE I TRAINING:
weight[0] = 0.262463 weight[1] = 1.30687 weight[2] = 1.32345 weight[3] = 0.929833
weight[4] = -1.40295 weight[5] = 1.46973 weight[6] = 4.50657 weight[7] = 6.25732
weight[8] = 2.05971 weight[9] = 2.55983 weight[10] = 3.40746 weight[11] = 3.52705
weight[12] = 0.371129 weight[13] = 3.43777 weight[14] = -0.526312 weight[15] = 1.41332
weight[16] = 4.33401 weight[17] = 6.28003 weight[18] = 3.69105
STAGE I TRAINING CONVERGED
STAGE I ERROR SS = 0.000000
GRADIENT AT THE OPTIMUM WEIGHTS
g[0] = 0.000001 weight[0] = 0.262463
g[1] = -0.000023 weight[1] = 1.306865
g[2] = 0.000027 weight[2] = 1.323447
g[3] = 0.000007 weight[3] = 0.929833
g[4] = 0.000010 weight[4] = -1.402949
g[5] = -0.000216 weight[5] = 1.469729
g[6] = 0.000249 weight[6] = 4.506571
g[7] = 0.000063 weight[7] = 6.257323
g[8] = -0.000002 weight[8] = 2.059708
g[9] = 0.000033 weight[9] = 2.559830
g[10] = -0.000038 weight[10] = 3.407457
g[11] = -0.000010 weight[11] = 3.527051
g[12] = 0.000049 weight[12] = 0.371129
g[13] = 0.000399 weight[13] = 3.437771
g[14] = 0.000235 weight[14] = -0.526312
g[15] = 0.000005 weight[15] = 1.413319
g[16] = 0.000043 weight[16] = 4.334013
g[17] = -0.000007 weight[17] = 6.280032
g[18] = 0.000012 weight[18] = 3.691053
Training Completed
Predictions for Last Ten Observations:
observation[90] 49.297478 Prediction 49.297482 Residual 0.000004
observation[91] 32.435097 Prediction 32.435097 Residual 0.000000
observation[92] 37.817757 Prediction 37.817760 Residual 0.000004
observation[93] 38.506630 Prediction 38.506630 Residual 0.000000
observation[94] 48.623795 Prediction 48.623802 Residual 0.000008
observation[95] 37.623909 Prediction 37.623913 Residual 0.000004
observation[96] 41.569431 Prediction 41.569435 Residual 0.000004
observation[97] 36.828972 Prediction 36.828976 Residual 0.000004
observation[98] 48.690826 Prediction 48.690826 Residual 0.000000
observation[99] 32.048107 Prediction 32.048107 Residual 0.000000
Bias: 15.809660
X1: 9.999999
X2: 19.999996
X3: 30.000000
X4: 20.000002
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |