bvp_finite_difference

Chapter 5: Differential Equations > bvp_finite_difference

bvp_finite_difference

Solves a (parameterized) system of differential equations with boundary conditions at two points, using a variable order, variable step size finite difference method with deferred corrections.

Synopsis

#include <imsl.h>

void imsl_f_bvp_finite_difference (void fcneq(), void fcnjac(), void fcnbc(), int n, int nleft, int ncupbc, float tleft, float tright, int linear, float *nfinal, float *xfinal, float *yfinal, …, 0)

The type double function is imsl_d_bvp_finite_difference.

Required Arguments

void fcneq (int n, float t, float y[], float p, float dydt[]) (Input)
User supplied function to evaluate derivatives.

int n (Input)
Number of differential equations.

float t (Input)
Independent variable, t.

float y[] (Input)
Array of size n containing the dependent variable values, y(t).

float p (Input)
Continuation parameter, p. See optional argument IMSL_PROBLEM_EMBEDDED.

float dydt[] (Output)
Array of size n containing the derivatives y′(t).

void fcnjac(int n, float t, float y[], float p, float dypdy[]) (Input)
User supplied function to evaluate the Jacobian.

int n (Input)
Number of differential equations.

float t (Input)
Independent variable, t.

float y[] (Input)
Array of size n containing the dependent variable values, y(t).

float p (Input)
Continuation parameter, p. See optional argument IMSL_PROBLEM_EMBEDDED.

float dypdy[] (Output)
n by n array containing the partial derivatives ai_,j = ∂ fi/ ∂ yjevaluated at (t, y). The values ai,j are returned in dypdy[(i-1)*n+(j-1)].

void fcnbc(int n, float yleft[], float yright[], float p, float h[]) (Input)
User supplied function to evaluate the boundary conditions.

int n (Input)
Number of differential equations.

float yleft[] (Input)
Array of size n containing the values of the dependent variable at the left endpoint.

float yright[] (Input)
Array of size n containing the values of the dependent variable at the right endpoint.

float p (Input)
Continuation parameter, p See optional argument IMSL_PROBLEM_EMBEDDED.

float h[] (Output)
Array of size n containing the boundary condition residuals. The boundary conditions are defined by hi= 0, for i = 0, …, n-1. The left endpoint conditions must be defined first, then, the conditions involving both endpoints, and finally the right endpoint conditions.

int n (Input)
Number of differential equations.

int nleft (Input)
Number of initial conditions. The value nleft must be greater than or equal to zero and less than n.

int ncupbc (Input)
Number of coupled boundary conditions. The value nleft + ncupbc must be greater than zero and less than or equal to n.

float tleft (Input)
The left endpoint.

float tright (Input)
The right endpoint.

int linear (Input)
Integer flag to indicate if the differential equations and the boundary conditions are linear. Set linear to one if the differential equations and the boundary conditions are linear, otherwise set linear to zero.

int *nfinal (Output)
Number of final grid points, including the endpoints.

float *tfinal (Output)
Array of size mxgrid containing the final grid points. Only the first nfinal points are significant. See optional argument IMSL_MAX_SUBINTER for definition of mxgrid.

float *yfinal (Output)
Array of size mxgrid by n containing the values of Y at the points in tfinal. See optional argument IMSL_MAX_SUBINTER for definition of mxgrid.

Synopsis with Optional Arugments

#include <imsl.h>

void imsl_f_bvp_finite_difference (void fcneq(), void fcnjac(), void fcnbc(), int n, int nleft, int ncupbc, float tleft, float tright, int linear, float *nfinal, float *xfinal[], float *yfinal,

IMSL_TOL, float tol,

IMSL_HINIT, int ninit, float tinit[], float yinit[][],

IMSL_PRINT, int iprint,

IMSL_MAX_SUBINTER, int mxgrid,

IMSL_PROBLEM_EMBEDDED, float pistep, void fcnpeq(), void fcnpbc(),

IMSL_ERR_EST, float **errest,

IMSL_ERR_EST_USER, float errest[],

IMSL_FCN_W_DATA, void fcneq(), void *data,

IMSL_JACOBIAN_W_DATA, void fcnjac (),void *data,

IMSL_FCN_BC_W_DATA, void fcnbc(), void *data,

IMSL_PROBLEM_EMBEDDED_W_DATA, float pistep,(), void *data, void fcnpeq(), void fcnpbc(), void *data,

Optional Arguments

IMSL_TOL, float tol (Input)
Relative error control parameter. The computations stop when

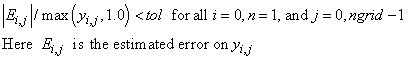
Default: tol = .001.

IMSL_HINIT, int ninit, float tinit[], float yinit[][], (Input)
Initial gridpoints. Number of initial grid points, including the endpoints, is given by ninit. tinit is an array of size ninit containing the initial grid points. yinit is an array size ninit by n containing an initial guess for the values of Y at the points in tinit.
Default: ninit = 10, tinit[*] equally spaced in the interval [tleft, tright], and yinit[*][*] = 0.

IMSL_PRINT, int iprint (Input)
Parameter indicating the desired output level.

iprint	Action
0	No output printed.
1	Intermediate output is printed. Default: iprint = 0.

iprint

Action

No output printed.

Intermediate output is printed.

Default: iprint = 0.

IMSL_MAX_SUBINTER, int mxgrid (Input)
Maximum number of grid points allowed.
Default: mxgrid = 100.

IMSL_PROBLEM_EMBEDDED, float pistep, void fcnpeq(), void fcnpbc()
If this optional argument is supplied, then the function imsl_f_bvp_finite_difference assumes that the user has embedded the problem into a one-parameter family of problems:

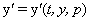
such that for p = 0 the problem is simple. For p = 1, the original problem is recovered. The function imsl_f_bvp_finite_difference automatically attempts to increment from p = 0 to p = 1. The value pistep is the beginning increment used in this continuation. The increment will usually be changed by function imsl_f_bvp_finite_difference, but an arbitrary minimum of 0.01 is imposed.

The argument p is the initial increment size for p. The functions fcnpeq and fcnpbc are user-supplied functions, and are defined:

void fcnpeq(int n, float t, float y[], float p, float dypdp[]) (Input)
User supplied function to evaluate the derivative of y′ with respect to the parameter p.

int n (Input)
Number of differential equations.

float t (Input)
Independent variable, t.

float y[] (Input)
Array of size n containing the dependent variable values.

float p (Input)
Continuation parameter, p.

float dypdp[] (Output)
Array of size n containing the derivative y′ with respect to the parameter p at (t, y).

void fcnpbc(int n, float yleft[], float yright[], float p, float h[])(Input)
User supplied function to evaluate the derivative of the boundary conditions with respect to the parameter p.

int n (Input)
Number of differential equations.

float yleft[] (Input)
Array of size n containing the values of the dependent variable at the left endpoint.

float yright[] (Input)
Array of size n containing the values of the dependent variable at the right endpoint.

float p (Input)
Continuation parameter, p.

float h[] (Output)
Array of size n containing the derivative of fi with respect to p.

IMSL_ERR_EST, float **errest (Output)
Address of a pointer to an array of size n containing estimated error in y.

IMSL_ERR_EST_USER, float errest[] (Output)
User allocated array of size n containing estimated error in y.

IMSL_FCN_W_DATA, void fcneq (int n, float t, float y[], float p, float dydt[], void *data) ,void *data, (Input)
User-supplied function to evaluate derivatives, which also accepts a pointer to data that is supplied by the user. data is a pointer to the data to be passed to the user-supplied function. See the Introduction, Passing Data to User-Supplied Functions at the beginning of this manual for more details.

IMSL_JACOBIAN_W_DATA, void fcnjac(int n, float t, float y[], float p, float dypdy[], void *data), void *data, (Input)
User-supplied function to evaluate the Jacobian, which also accepts a pointer to data that is supplied by the user. data is a pointer to the data to be passed to the user-supplied function. See the Introduction, Passing Data to User-Supplied Functions at the beginning of this manual for more details.

IMSL_FCN_BC_W_DATA, void fcnbc(int n, float yleft[], float yright[], float p, float h[], void *data), void *data, (Input)
User-supplied function to evaluate the boundary conditions , which also accepts a pointer to data that is supplied by the user. data is a pointer to the data to be passed to the user-supplied function. See the Introduction, Passing Data to User-Supplied Functions at the beginning of this manual for more details.

IMSL_PROBLEM_EMBEDDED_W_DATA, float pistep, void fcnpeq(void *data), void fcnpbc(), void *data, (Input)
Same as optional argument IMSL_PROBLEM_EMBEDDED, except user-supplied functions also accept a pointer to data that is supplied by the user. data is a pointer to the data to be passed to the user-supplied function. See the Introduction, Passing Data to User-Supplied Functions at the beginning of this manual for more details.

Description

The function imsl_f_bvp_finite_difference is based on the subprogram PASVA3 by M. Lentini and V. Pereyra (see Pereyra 1978). The basic discretization is the trapezoidal rule over a nonuniform mesh. This mesh is chosen adaptively, to make the local error approximately the same size everywhere. Higher-order discretizations are obtained by deferred corrections. Global error estimates are produced to control the computation. The resulting nonlinear algebraic system is solved by Newton’s method with step control. The linearized system of equations is solved by a special form of Gauss elimination that preserves the sparseness.

Example 1

This example solves the third-order linear equation

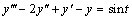
subject to the boundary conditions y(0) = y(2π) and y′(0) = y′(2π) = 1. (Its solution is y = sin t.) To use imsl_f_bvp_finite_difference, the problem is reduced to a system of first-order equations by defining y1 = y, y2 = y′ and y3 = y″. The resulting system is

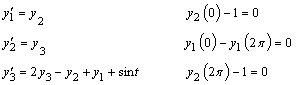
Note that there is one boundary condition at the left endpoint t = 0 and one boundary condition coupling the left and right endpoints. The final boundary condition is at the right endpoint. The total number of boundary conditions must be the same as the number of equations (in this case 3).

#include <math.h>

#include <imsl.h>

void fcneqn( int n, float t, float y[], float p, float dydt[]);

void fcnjac( int n, float t, float y[], float p, float dfdy[]);

void fcnbc( int n, float yleft[], float yright[], float p, float h[]);

#define MXGRID 100

#define N 3

int main()

{

int n = N;

int nleft = 1;

int ncupbc = 1;

float tleft = 0;

float tright;

int linear = 1;

int nfinal;

float tfinal[MXGRID];

float yfinal[MXGRID][N];

float errest[N];

int i;

tright = 2.0*imsl_f_constant("pi", 0);

imsl_f_bvp_finite_difference( fcneqn, fcnjac, fcnbc,

n, nleft, ncupbc, tleft, tright,

linear, &nfinal, tfinal,

(float*)(&yfinal[0][0]),

IMSL_ERR_EST_USER, errest,

0);

printf(" tfinal y0 y1 y2 \n" );

for( i=0; i<nfinal; i++ ) {

printf( "%5d%15.6e%15.6e%15.6e%15.6e\n", i, tfinal[i],

yfinal[i][0], yfinal[i][1], yfinal[i][2] );

}

printf("Error Estimates ");

printf("%15.6e%15.6e%15.6e\n",errest[0],errest[1],errest[2]);

return;

}

void fcneqn( int n, float t, float y[], float p, float dydt[] )

{

dydt[0] = y[1];

dydt[1] = y[2];

dydt[2] = 2*y[2] - y[1] + y[0] + sin(t);

}

void fcnjac( int n, float t, float y[], float p, float dfdy[] )

{

dfdy[0*n+0] = 0; /* df1/dy1 */

dfdy[1*n+0] = 0; /* df2/dy1 */

dfdy[2*n+0] = 1; /* df3/dy1 */

dfdy[0*n+1] = 1; /* df1/dy2 */

dfdy[1*n+1] = 0; /* df2/dy2 */

dfdy[2*n+1] = -1; /* df3/dy2 */

dfdy[0*n+2] = 0; /* df1/dy3 */

dfdy[1*n+2] = 1; /* df2/dy3 */

dfdy[2*n+2] = 2; /* df3/dy3 */

}

void fcnbc( int n, float yleft[], float yright[], float p, float h[] )

{

h[0] = yleft[1] - 1;

h[1] = yleft[0] - yright[0];

h[2] = yright[1] - 1;

}

Output

tfinal y0 y1 y2

0 0.000000e+00 -1.123446e-04 1.000000e+00 6.245916e-05

1 3.490659e-01 3.419106e-01 9.397087e-01 -3.419581e-01

2 6.981317e-01 6.426907e-01 7.660918e-01 -6.427230e-01

3 1.396263e+00 9.847531e-01 1.737333e-01 -9.847453e-01

4 2.094395e+00 8.660527e-01 -4.998748e-01 -8.660057e-01

5 2.792527e+00 3.421828e-01 -9.395475e-01 -3.420647e-01

6 3.490659e+00 -3.417236e-01 -9.396111e-01 3.418948e-01

7 4.188790e+00 -8.656881e-01 -5.000588e-01 8.658734e-01

8 4.886922e+00 -9.845795e-01 1.734572e-01 9.847519e-01

9 5.585054e+00 -6.427722e-01 7.658259e-01 6.429526e-01

10 5.934120e+00 -3.420819e-01 9.395434e-01 3.423984e-01

11 6.283185e+00 -1.123446e-04 1.000000e+00 6.739637e-04

Error Estimates 2.840487e-04 1.792839e-04 5.587848e-04

Example 2

In this example, the following nonlinear problem is solved:

y″ − y3 + (1 + sin2t) sin t = 0

with y(0) = y(π) = 0. Its solution is y = sin t. As in Example 1, this equation is reduced to a system of first-order differential equations by defining y1 = y and y2 = y′. The resulting system is

In this problem, there is one boundary condition at the left endpoint and one at the right endpoint; there are no coupled boundary conditions.

#include <math.h>

#include <imsl.h>

void fcneqn(int n, float x, float y[], float p, float dydx[]);

void fcnjac(int n, float x, float y[], float p, float dfdy[]);

void fcnbc(int n, float yleft[], float yright[], float p, float h[]);

#define MXGRID 100

#define NINIT 12

#define N 2

int main()

{

int n = N, nleft = 1, ncupbc = 0, linear = 0;

int i, nfinal, ninit = NINIT;

float tleft = 0, tright;

float tinit[NINIT], yinit[NINIT][N];

float tfinal[MXGRID], yfinal[MXGRID][N];

float *errest, step;

tright = imsl_f_constant("pi", 0);

step = (tright-tleft) / (ninit-1);

for( i=0; i<ninit; i++ ) {

tinit[i] = tleft + i*step;

yinit[i][0] = 0.4 * (tinit[i]-tleft) * (tright-tinit[i]);

yinit[i][1] = 0.4 * (tright+tleft-2*tinit[i]);

}

imsl_f_bvp_finite_difference(fcneqn, fcnjac, fcnbc,

n, nleft, ncupbc, tleft, tright,

linear, &nfinal, tfinal,

(float*)(&yfinal[0][0]),

IMSL_HINIT, ninit, tinit, yinit,

IMSL_ERR_EST, &errest,

0);

printf(" t y0 y1\n" );

for( i=0; i<nfinal; i++ ) {

printf( "%5d%15.6e%15.6e%15.6e\n", i, tfinal[i], yfinal[i][0],

yfinal[i][1]);

}

printf("Error Estimates ");

printf("%15.6e%15.6e\n",errest[0],errest[1]);

return;

}

void fcneqn(int n, float t, float y[], float p, float dydt[])

{

float sx = sin(t);

dydt[0] = y[1];

dydt[1] = y[0]*y[0]*y[0] - (sx*sx+1)*sx;

}

void fcnjac(int n, float t, float y[], float p, float dfdy[])

{

dfdy[0*n+0] = 0; /* df1/dy1 */

dfdy[1*n+0] = 3*y[0]*y[0]; /* df2/dy1 */

dfdy[0*n+1] = 1; /* df1/dy2 */

dfdy[1*n+1] = 0; /* df2/dy2 */

}

void fcnbc(int n, float yleft[], float yright[], float p, float h[])

{

h[0] = yleft[0];

h[1] = yright[0];

}

Output

t y0 y1

0 0.000000e+00 0.000000e+00 9.999277e-01

1 2.855994e-01 2.817682e-01 9.594315e-01

2 5.711987e-01 5.406458e-01 8.412407e-01

3 8.567981e-01 7.557380e-01 6.548904e-01

4 1.142397e+00 9.096186e-01 4.154530e-01

5 1.427997e+00 9.898143e-01 1.423307e-01

6 1.713596e+00 9.898143e-01 -1.423308e-01

7 1.999195e+00 9.096185e-01 -4.154530e-01

8 2.284795e+00 7.557380e-01 -6.548902e-01

9 2.570394e+00 5.406460e-01 -8.412405e-01

10 2.855994e+00 2.817682e-01 -9.594312e-01

11 3.141593e+00 0.000000e+00 -9.999274e-01

Error Estimates 3.907291e-05 7.124317e-05

Example 3

In this example, the following nonlinear problem is solved:

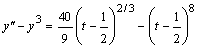
with y(0) = y(1) = π/2. As in the previous examples, this equation is reduced to a system of first-order differential equations by defining y1 = y and y2 = y′. The resulting system is

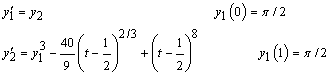
The problem is embedded in a family of problems by introducing the parameter p and by changing the second differential equation to

At p = 0, the problem is linear; and at p = 1, the original problem is recovered. The derivatives ∂y′/∂p must now be specified in the subroutine fcnpeq. The derivatives ∂f/∂p are zero in fcnpbc.

#include <stdio.h>

#include <math.h>

#include <imsl.h>

void fcneqn(int n, float t, float y[], float p, float dydt[]);

void fcnjac(int n, float t, float y[], float p, float dfdy[]);

void fcnbc(int n, float yleft[], float yright[], float p, float h[]);

void fcnpeq(int n, float t, float y[], float p, float dfdp[]);

void fcnpbc(int n, float yleft[], float yright[], float p, float dhdp[]);

#define MXGRID 45

#define NINIT 12

#define N 2

int main()

{

int n = 2;

int nleft = 1;

int ncupbc = 0;

float tleft = 0;

float tright = 1;

float pistep = 0.1;

int ninit = 5;

float tinit[NINIT] = { 0.0, 0.4, 0.5, 0.6, 1.0 };

float yinit[NINIT][N] = { 0.15749, 0.00215,

0.0, 0.00215,

0.15749, -0.83995,

-0.05745, 0.0,

0.05745, 0.83995 };

int linear = 0;

int nfinal;

float tfinal[MXGRID];

float yfinal[MXGRID][N];

float *errest;

int i;

imsl_f_bvp_finite_difference( fcneqn, fcnjac, fcnbc, n, nleft,

ncupbc, tleft, tright,

linear, &nfinal, tfinal, (float*)(&yfinal[0][0]),

IMSL_MAX_SUBINTER, MXGRID,

IMSL_PROBLEM_EMBEDDED, pistep, fcnpeq, fcnpbc,

IMSL_HINIT, ninit, tinit, yinit,

IMSL_ERR_EST, &errest,

0 );

printf(" t y0 y1\n" );

for( i=0; i<nfinal; i++ ) {

printf("%5d%15.6e%15.6e%15.6e\n", i, tfinal[i], yfinal[i][0],

yfinal[i][1]);

}

printf("Error Estimates ");

printf("%15.6e%15.6e\n",errest[0],errest[1]);

return;

}

void fcneqn(int n, float t, float y[], float p, float dydt[])

{

float z = t - 0.5;

dydt[0] = y[1];

dydt[1] = p*y[0]*y[0]*y[0] + 40./9.*pow(z*z,1./3.) - pow(z,8);

}

void fcnjac(int n, float t, float y[], float p, float dfdy[])

{

dfdy[0*n+0] = 0; /* df0/dy0 */

dfdy[0*n+1] = 1; /* df0/dy1 */

dfdy[1*n+0] = 3.*(p)*(y[0]*y[0]); /* df1/dy0 */

dfdy[1*n+1] = 0; /* df1/dy1 */

}

void fcnbc(int n, float yleft[], float yright[], float p, float h[])

{

float pi2 = imsl_f_constant("pi", 0)/2.0;

h[0] = yleft[0] - pi2;

h[1] = yright[0] - pi2;

}

void fcnpeq(int n, float t, float y[], float p, float dfdp[])

{

dfdp[0] = 0;

dfdp[1] = y[0]*y[0]*y[0];

}

void fcnpbc(int n, float yleft[], float yright[], float p, float dhdp[])

{

dhdp[0] = 0;

dhdp[1] = 0;

}

Output

t y0 y1

0 0.000000e+000 1.570796e+000 -1.949336e+000

1 4.444445e-002 1.490495e+000 -1.669567e+000

2 8.888889e-002 1.421951e+000 -1.419465e+000

3 1.333333e-001 1.363953e+000 -1.194307e+000

4 2.000000e-001 1.294526e+000 -8.958461e-001

5 2.666667e-001 1.243628e+000 -6.373191e-001

6 3.333334e-001 1.208785e+000 -4.135206e-001

7 4.000000e-001 1.187783e+000 -2.219351e-001

8 4.250000e-001 1.183038e+000 -1.584200e-001

9 4.500000e-001 1.179822e+000 -9.973147e-002

10 4.625000e-001 1.178748e+000 -7.233894e-002

11 4.750000e-001 1.178007e+000 -4.638249e-002

12 4.812500e-001 1.177756e+000 -3.399764e-002

13 4.875000e-001 1.177582e+000 -2.205549e-002

14 4.937500e-001 1.177480e+000 -1.061179e-002

15 5.000000e-001 1.177447e+000 -1.603742e-007

16 5.062500e-001 1.177480e+000 1.061152e-002

17 5.125000e-001 1.177582e+000 2.205516e-002

18 5.187500e-001 1.177756e+000 3.399726e-002

19 5.250000e-001 1.178007e+000 4.638217e-002

20 5.375000e-001 1.178748e+000 7.233874e-002

21 5.500000e-001 1.179822e+000 9.973122e-002

22 5.750000e-001 1.183038e+000 1.584198e-001

23 6.000000e-001 1.187783e+000 2.219350e-001

24 6.666667e-001 1.208786e+000 4.135205e-001

25 7.333333e-001 1.243628e+000 6.373190e-001

26 8.000000e-001 1.294526e+000 8.958460e-001

27 8.666667e-001 1.363953e+000 1.194307e+000

28 9.111111e-001 1.421951e+000 1.419465e+000

29 9.555556e-001 1.490495e+000 1.669566e+000

30 1.000000e+000 1.570796e+000 1.949336e+000

Error Estimates 3.449248e-006 5.550227e-005

Contact Support