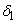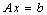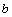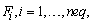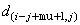Solves a first order differential-algebraic system of equations, g(t, y, yʹ) = 0, with optional additional constraints and user-defined linear system solver.
Note: imsl_f_differential_algebraic_eqs replaces imsl_f_dea_petzold_gear.
Synopsis
#include <imsl.h>
void imsl_f_differential_algebraic_eqs (int neq, float *t, float tend, int *ido, float y[], float yprime[], void gcn(), ..., 0)
The type double function is imsl_d_differential_algebraic_eqs.
Required Arguments
int neq
(Input)
Number of dependent variables, and number of differential/algebraic
equations, not counting any additional constraints.
float *t
(Input/Output)
Set t to the starting
value t0 at the first step. On output, t is set to the value
to which the integration has advanced. Normally, this new value is tend.
float tend
(Input)
Final value of the independent variable. Update
this value when re-entering after output with ido = 2.
int *ido
(Input/Output)
Flag indicating the state of the computation.
|
ido |
State |
|
1 |
Initial entry |
|
2 |
Normal re-entry after obtaining output |
|
3 |
Release workspace, last call |
The user sets ido = 1 on the first call at t = t0. The function then sets ido =2, and this value is used for all but the last entry, which is made with ido = 3.
float y[] (Input/Output)
Array of length neq containing the
dependent variable values, y. On input, y must contain initial
values. On output, y contains the
computed solution at tend.
float yprime[] (Input/Output)
Array of length neq containing
derivative values, yʹ. This array
must contain initial values, but they need not be such that
g(t, y, yʹ) = 0
at t =t0. See the
description of parameter iypr for
more information.
void gcn
(int neq,
float t,
float y[],
float yprime[],
float delta[],
float d[],
int ldd,
int *ires) (Input)
User-supplied function to
evaluate g(t, y, yʹ), and any
constraints. Also partial derivative evaluations and optionally linear solving
steps occur here. The equations
g(t, y, yʹ) = 0
consist of neq
differential-algebraic equations of the form.
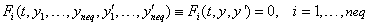
The function gcn is also used to evaluate the ncon additional algebraic constraints.
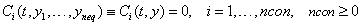
Arguments
int neq
(Input)
Number of dependent variables, and number of differential-algebraic
equations, not counting any additional constraints.
float t (Input)
Integration variable
t.
float y[]
(Input)
Array of neq dependent
variables, y.
float yprime[] (Input)
Array of neq derivative values,
yʹ.
float delta[]
(Input/Output)
Array of length max(neq, ncon) containing
residuals, 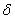 . See parameter ires for a
definition.
. See parameter ires for a
definition.
float d[] (Input/Output
Array of length ldd × neq containing partial
derivatives, d See parameter ires for a
definition.
int ldd
(Input)
Number of rows in d.
int *ires
(Input/Output)
Flag indicating what is to be calculated in the user function,
gcn.
Note: ires is input only, except when ires = 6. It is input/output when ires = 6. For a detailed description see the table below.
The code calls gcn with ires = 0, 1, 2, 3, 4, 5, 6, or 7, defined as follows:
|
ires |
Description |
|
0 |
Do initializations which may be required in later calls to gcn. This is a setup flag that is input to gcn just once per problem. Initializations might be computing parameters to be used internally by gcn or taking any other necessary steps for what may follow in terms of evaluating derivatives or linear solves. Return and do nothing if no initializations are needed. |
|
1 |
Compute |
|
2 |
(Required only if iujac =1 and matstr = 0 or 1).
the partial derivative matrix. These
are derivatives of |
|
3 |
(Required only if iujac =1 and matstr = 0 or 1).
the partial derivative of |
|
4 |
(Required only if iypr = 2).
the partial derivative of Fi with respect to t, for i =1,…, neq. |
|
5 |
(Required only if ncon > 0).
the partial derivative of |
|
(Required only if isolve = 1.) If matstr = 2, the user must compute the matrix
where cj = If matstr = 0 or 1, the A matrix will already be defined and passed to gcn in the array d, which will be in full matrix format if matstr = 0, and band matrix format, if matstr = 1. The user may factor d in this step, if desired. Note: For matstr = 0, 1, or 2, the user must set ires = 0 to signal that A is nonsingular. If A is nearly singular, leave ires = 6. This results in using a smaller step-size internally. | |
|
7 |
(Required only if isolve = 1.) The user must solve |
Synopsis with Optional Arguments
#include <imsl.h>
void imsl_f_differential_algebraic_eqs (int neq, float *t, float tend, int *ido, float y[], float yprime[], void gcn(),
IMSL_N_CONSTRAINTS, int ncon,
IMSL_JACOBIAN_OPTION, int iujac,
IMSL_YPRIME_METHOD, int iypr,
IMSL_JACOBIAN_MATRIX_TYPE, int matstr,
IMSL_METHOD, int isolve,
IMSL_N_LOWER_DIAG, int ml,
IMSL_N_UPPER_DIAG, int mu,
IMSL_RELATIVE_TOLERANCE, float rtol,
IMSL_ABSOLUTE_TOLERANCE, float atol[],
IMSL_INITIAL_STEPSIZE, float h0,
IMSL_MAX_STEPSIZE, float hmax,
IMSL_MAX_ORDER, int maxord,
IMSL_MAX_NUMBER_STEPS, int maxsteps,
IMSL_INTEGRATION_LIMIT, float tstop,
IMSL_ORDER_MAGNITUDE_EST, float fmag,
IMSL_GCN_W_DATA, void gcn(), void *data,
0)
Optional Arguments
IMSL_N_CONSTRAINTS,
int ncon (Input)
Number
of additional constraints.
Default: ncon = 0.
IMSL_JACOBIAN_OPTION,
int iujac
(Input)
Jacobian calculation option.
|
iujac |
Description |
|
0 |
Calculates using finite difference approximations. |
|
1 |
User supplies the Jacobian matrices of partial
derivatives of |
Default: iujac = 0 for matstr = 0 or 1. iujac = 1 for matstr = 2.
IMSL_YPRIME_METHOD,
int iypr
(Input)
Initial yʹ calculation
method.
|
iypr |
Description |
|
0 |
The initial input values of yprime are already consistent with the input values of Y. That is g(t, y, yʹ) = 0 at t = t0. Any constraints must be satisfied at t = t0. |
|
1 |
Consistent values of yprime are calculated by Petzold’s original DASSL algorithm. |
|
2 |
Consistent values of yprime are calculated using a new algorithm [Hanson and Krogh, 2008], which is generally more robust but requires that iujac = 1 and isolve = 0, and additional derivatives corresponding to ires = 4 are to be calculated in gcn. |
Default: iypr = 1.
IMSL_JACOBIAN_MATRIX_TYPE,
int matstr
(Input)
Parameter specifying the Jacobian matrix structure.
|
matstr |
Description |
|
0 |
The Jacobian matrices (whether iujac = 0 or 1) are to be stored in full storage mode. |
|
1 |
The Jacobian matrices are to be stored in band
storage mode. In this case, if iujac = 1, the partial derivative matrices
have their entries for row i and column j, stored as
array elements |
|
2 |
A user-defined matrix structure is used (see the documentation for ires = 6 or 7 for more details). If matstr = 2, isolve and iujac are set to 1 internally. |
Default: matstr = 0.
IMSL_METHOD,
int isolve
(Input)
Solve method.
|
isolve |
Description |
|
0 |
imsl_f_differential_algebraic_eqs solves the linear systems. |
|
1 |
The user wishes to solve the linear system in function gcn. See parameter gcn for details. |
Default: isolve = 0 for matstr = 0 or 1. isolve = 1 for matstr = 2.
IMSL_N_LOWER_DIAG,
int ml (Input)
Number
of non-zero diagonals below the main diagonal in the Jacobian matrices when band
storage mode is used. ml is ignored if matstr ≠ 1.
Default:
ml = neq - 1.
IMSL_N_UPPER_DIAG,
int mu (Input)
Number
of non-zero diagonals above the main diagonal in the Jacobian matrices when band
storage mode is used. mu is ignored if matstr ≠ 1.
Default:
mu = neq - 1.
IMSL_RELATIVE_TOLERANCE,
float rtol
(Input)
Relative error tolerance for solver. The program attempts to maintain
a local error in Y(i) less than rtol*│y[i]│ + atol[i].
Default:
rtol = 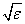 , where
, where 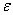 is
machine precision.
is
machine precision.
IMSL_ABSOLUTE_TOLERANCE,
float atol[]
(Input)
Array of size neq containing
absolute error tolerances. See description of rtol.
Default:
atol[i] = 0.0.
IMSL_INITIAL_STEPSIZE,
float h0 (Input)s
Initial
stepsize used by the solver. If h0 = 0.0,
the function defines the initial stepsize.
Default: h0 = 0.0.
IMSL_MAX_STEPSIZE,
float hmax
(Input)
Maximum stepsize used by the solver. If hmax = 0.0,
the function defines the maximum stepsize.
Default: hmax = 0.0.
IMSL_MAX_ORDER,
int maxord
(Input)
Maximum order of the backward difference formulas used.
1 ≤ maxord ≤ 5.
Default:
maxord = 5.
IMSL_MAX_NUMBER_STEPS,
int maxsteps
(Input)
Maximum number of steps allowed from t to tend.
Default:
maxsteps = 500.
IMSL_INTEGRATION_LIMIT,
float tstop
(Input)
Integration limit point. For efficiency reasons, the code
sometimes integrates past tend and interpolates
a solution at tend. If a value for
tstop is
specified, the code will never integrate past t=tstop.
Default: No
tstop value is
specified.
IMSL_ORDER_MAGNITUDE_EST,
float fmag
(Input)
Order-of-magnitude estimate. fmag is used as an
order-of-magnitude estimate of the magnitude of the functions Fi (see
description of gcn), for convergence
testing, if iypr=2. fmag is ignored if
iypr=0 or
1.
Default: fmag = 1.0.
IMSL_GCN_W_DATA,
void gcn(int neq,
float t,
float y[],
float yprime[],
float delta[],
float d[],
int ldd,
int *ires,
void *data),
void *data
(Input)
User-supplied function to evaluate
g(t, y, yʹ), and any
constraints, which also accepts a pointer to data that is supplied by the user.
data is a
pointer to the data to be passed to the user-supplied function. Please refer to
gcn in the Required
Arguments section for more information. See the Introduction, Passing Data
to User-Supplied Functions at the beginning of this manual for more
details.
Description
Function imsl_f_differential_algebraic_eqs
finds an approximation to the solution of a system of differential-algebraic
equations 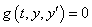 with given initial data for
with given initial data for 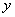 and
and 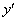 . The function uses BDF formulas,
which are appropriate for stiff systems. imsl_f_differential_algebraic_eqs
is based on the code DASSL
designed by Linda Petzold [1982], and has been modified by Hanson and Krogh
[2008] Solving
Constrained Differential-Algebraic Systems Using Projections to allow
the inclusion of additional constraints, including conservation principles,
after each time step. The modified code also provides a more robust
algorithm to calculate initial
. The function uses BDF formulas,
which are appropriate for stiff systems. imsl_f_differential_algebraic_eqs
is based on the code DASSL
designed by Linda Petzold [1982], and has been modified by Hanson and Krogh
[2008] Solving
Constrained Differential-Algebraic Systems Using Projections to allow
the inclusion of additional constraints, including conservation principles,
after each time step. The modified code also provides a more robust
algorithm to calculate initial 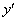 values consistent with
the given initial
values consistent with
the given initial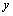 values. This occurs when
the initial
values. This occurs when
the initial 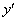 are not known.
are not known.
A differential-algebraic system of equations is said to
have “index 0” if the Jacobian matrix of partial derivatives of the 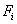 with respect to the
with respect to the 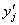 is nonsingular. Thus it is
possible to solve for all the initial values of
is nonsingular. Thus it is
possible to solve for all the initial values of 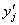 and put the system in the form of
a standard ODE system. If it is possible to reduce the system to a
system of index 0 by taking first derivatives of some of the equations, the
system has index 1, otherwise the index is greater than 1. See Brenan
[1989] for a definition of index. imsl_f_differential_algebraic_eqs
can generally only solve systems of index 0 or 1; other systems will usually
have to be reduced to such a form through differentiation.
and put the system in the form of
a standard ODE system. If it is possible to reduce the system to a
system of index 0 by taking first derivatives of some of the equations, the
system has index 1, otherwise the index is greater than 1. See Brenan
[1989] for a definition of index. imsl_f_differential_algebraic_eqs
can generally only solve systems of index 0 or 1; other systems will usually
have to be reduced to such a form through differentiation.
Examples
Example 1 – Method of Lines PDE Problem
This example solves the partial differential
equation , with initial condition
, with initial condition 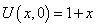 , and boundary conditions
, and boundary conditions 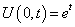 ,
, 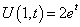 which has exact solution
which has exact solution 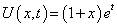 . If we approximate the
. If we approximate the  term using finite differences,
where
term using finite differences,
where 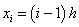 , and
, and  , we get:
, we get:
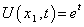
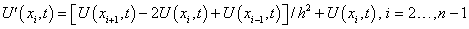
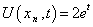
If Yi(t) = U(xi,t), the first and last equations are algebraic and the others are differential equations, so this is a system of differential-algebraic equations. The system has index = 1, since it could be transformed into an ODE system by differentiating the first and last equations. Note that the Jacobian matrices are banded (tridiagonal), with ml = mu = 1. We use this and specify the option for dealing with banded matrices in imsl_f_differential_algebraic_eqs.
#include <imsl.h>
#include <math.h>
#include <stdio.h>
#define NEQ 101
#define MAX(a,b) ((a) > (b)) ? (a) : (b)
void gcn(int neq, float t, float y[], float yprime[], float delta[],
float *d, int ldd, int *ires);
int main() {
int i, ido, iujac=1, iypr=1, matstr=1, ml=1, mu=1, nsteps=10;
float errmax=0.0, hx, rtol=1.0e-4, t, tend, tr, x,
y[NEQ], yprime[NEQ];
hx = 1.0 / (float) (NEQ - 1);
/* Initial values */
for (i = 0; i < NEQ; i++) {
yprime[i] = 0.0;
x = ((float) i) * hx;
y[i] = 1.0 + x;
}
/* Always set ido=1 on first call */
ido = 1;
for (i = 0; i < nsteps; i++) {
/* Output solution at t=0.1,0.2,...,1.0 */
t = 0.1 * (float) i;
tend = 0.1 * (float) (i + 1);
/* Set ido = 3 on last call */
if (i == (nsteps-1))
ido = 3;
/* User-supplied jacobian matrix (iujac=1)
Banded jacobian (matstr=1) */
imsl_f_differential_algebraic_eqs(NEQ, &t, tend, &ido, y,
yprime, gcn,
IMSL_JACOBIAN_OPTION, iujac,
IMSL_YPRIME_METHOD, iypr,
IMSL_JACOBIAN_MATRIX_TYPE, matstr,
IMSL_N_LOWER_DIAG, ml,
IMSL_N_UPPER_DIAG, mu,
IMSL_RELATIVE_TOLERANCE, rtol,
0);
}
for (i = 0; i < NEQ; i++) {
x = ((float) i) * hx;
tr = (1.0 + x) * exp(t);
errmax = MAX(errmax,fabs(y[i]-tr));
}
printf("Max Error at T=1 is %g.\n", errmax);
}
void gcn(int neq, float t, float y[], float yprime[], float delta[],
float *d, int ldd, int *ires) {
#define D(I_,J_) (*(d+(I_)*(neq)+(J_)))
int i, j, mu;
float hx;
hx = 1.0 / (float) (neq - 1);
mu = 1;
if (*ires == 1) {
/* f_i defined here */
delta[0] = y[0] - exp(t);
for (i = 1; i < (neq - 1); i++)
delta[i] = -yprime[i] + (y[i+1] - 2.0 * y[i] + y[i-1]) /
pow(hx,2) + y[i];
delta[neq-1] = y[neq-1] - 2.0 * exp(t);
} else if (*ires == 2) {
/* d(i-j+mu+1,j) = d(f_i)/d(y_j)
in band storage mode */
D(mu,0) = 1.0;
for (i = 1; i < (neq - 1); i++) {
j = i;
D(i-j+mu+1,j-1) = 1.0 / pow(hx,2);
j = i + 1;
D(i-j+mu+1,j-1) = -2.0 / pow(hx,2) + 1.0;
j = i + 2;
D(i-j+mu+1,j-1) = 1.0 / pow(hx,2);
}
D(mu,neq-1) = 1.0;
} else if (*ires == 3) {
/* d(i-j+mu+1,j) = d(f_i)/d(yprime_j ) */
for (i = 1; i < (neq - 1); i++)
D(mu,i) = -1.0;
}
}
Output
Max Error at T=1 is 5.53131e-005.
Example 2 – Pendulum Problem
The first-order equations of motion of a point-mass m
suspended on a massless wire of length 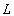 under the influence of
gravity, mg, and wire tension, λ , in Cartesian coordinates
(p,q) are
under the influence of
gravity, mg, and wire tension, λ , in Cartesian coordinates
(p,q) are
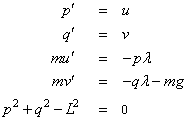
The problem above has an index number equal to 3, thus it cannot be solved with imsl_f_differential_algebraic_eqs directly. Unfortunately, the fact that the index is greater than 1 is not obvious, but an attempt to solve it will generally produce an error message stating the corrector equation did not converge, or if iypr = 2 an error message stating that the index appears to be greater than 1 should be issued. The user then differentiates the last equation, which after replacing pʹ by u and qʹ by v, gives pu+qv = 0. This system still has index=2 (again not obvious, the user discovers this by unsuccessfully trying to solve the new system) and the last equation must be differentiated again, to finally (after appropriate substitutions) give the equation of total energy balance:
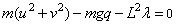
With initial conditions and appropriate definitions of the dependent variables, the system becomes:
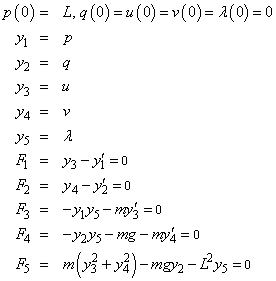
The initial conditions correspond to the pendulum starting in a horizontal position.
Since we have replaced the original constraint, 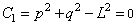 , which requires that the pendulum
length be L, by differentiating it twice, this constraint is no longer
explicitly enforced, and if we try to solve the above system alone (ie, with
ncon=0),
the pendulum length drifts substantially from L at larger times. imsl_f_differential_algebraic_eqs
therefore allows the user to add additional constraints, to be re-enforced after
each time step, so we add this original constraint, as well as the intermediate
constraint
, which requires that the pendulum
length be L, by differentiating it twice, this constraint is no longer
explicitly enforced, and if we try to solve the above system alone (ie, with
ncon=0),
the pendulum length drifts substantially from L at larger times. imsl_f_differential_algebraic_eqs
therefore allows the user to add additional constraints, to be re-enforced after
each time step, so we add this original constraint, as well as the intermediate
constraint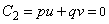 . Using these two supplementary
constraints, (ncon = 2),
the pendulum length is constant.
. Using these two supplementary
constraints, (ncon = 2),
the pendulum length is constant.
#include <imsl.h>
#include <math.h>
#include <stdio.h>
#define NEQ 5
void gcn(int neq, float t, float y[], float yprime[], float delta[],
float *d, int ldd, int *ires);
int main() {
int i, ido, ncon=2, nsteps=5, iypr=2, iujac=1, maxsteps=50000;
float atol[NEQ], len, t, tend, tol, y[NEQ], yprime[NEQ],
mass=1.0, length=1.1, gravity=9.806650;
/* Initial values */
tol = 1.0e-5;
for (i = 0; i < NEQ; i++) {
y[i] = 0.0;
yprime[i] = 0.0;
atol[i] = tol;
}
y[0] = length;
printf(" T Y(0) ");
printf("Y(1) Length\n");
/* Always set ido=1 on first call */
ido = 1;
for (i = 0; i < nsteps; i++) {
/* Output solution at t=10,20,30,40,50 */
t = 10.0 * (float) i;
tend = 10.0 * (float) (i + 1);
/* Set ido = 3 on last call*/
if (i == (nsteps-1))
ido = 3;
/* User-supplied jacobian matrix (iujac=1)
Use new algorithm to get compatible y' */
imsl_f_differential_algebraic_eqs(NEQ, &t, tend, &ido, y,
yprime, gcn,
IMSL_N_CONSTRAINTS, ncon,
IMSL_JACOBIAN_OPTION, iujac,
IMSL_YPRIME_METHOD, iypr,
IMSL_RELATIVE_TOLERANCE, tol,
IMSL_ABSOLUTE_TOLERANCE, atol,
IMSL_MAX_NUMBER_STEPS, maxsteps,
0);
/* len = pendulum length (should be constant) */
len = sqrt(pow(y[0],2) + pow(y[1],2));
printf("%15.7f %15.7f %15.7f %15.7f\n", t, y[0], y[1], len);
}
}
void gcn(int neq, float t, float y[], float yprime[], float delta[],
float *d, int ldd, int *ires) {
#define D(I_,J_) (*(d+(I_)*(neq)+(J_)))
float lsq, mg, mass=1.0, length=1.1, gravity=9.806650;
/* Simple swinging pendulum problem */
mg = mass * gravity;
lsq = pow(length,2);
if (*ires == 1) {
/* f_i defined here */
delta[0] = y[2] - yprime[0];
delta[1] = y[3] - yprime[1];
delta[2] = -y[0] * y[4] - mass * yprime[2];
delta[3] = -y[1] * y[4] - mass * yprime[3] - mg;
delta[4] = mass * (pow(y[2],2) + pow(y[3],2)) -
mg * y[1] - lsq * y[4];
} else if (*ires == 2) {
/* d(i,j) = d(f_i)/d(y_j) */
D(0,2) = 1.0;
D(1,3) = 1.0;
D(2,0) = -y[4];
D(2,4) = -y[0];
D(3,1) = -y[4];
D(3,4) = -y[1];
D(4,1) = -mg;
D(4,2) = mass * 2.0 * y[2];
D(4,3) = mass * 2.0 * y[3];
D(4,4) = -lsq;
} else if (*ires == 3) {
/* d(i,j) = d(f_i)/d(yprime_j) */
D(0,0) = -1.0;
D(1,1) = -1.0;
D(2,2) = -mass;
D(3,3) = -mass;
} else if (*ires == 4) {
/* delta(i) = d(f_i)/dt */
delta[0] = 0.0;
delta[1] = 0.0;
delta[2] = 0.0;
delta[3] = 0.0;
delta[4] = 0.0;
} else if (*ires == 5) {
/* delta(i) = g_i
d(i,j) = d(g_i)/d(y_j) */
delta[0] = pow(y[0],2) + pow(y[1],2) - lsq;
delta[1] = y[0]*y[2] + y[1]*y[3];
D(0,0) = 2.0 * y[0];
D(0,1) = 2.0 * y[1];
D(0,2) = 0.0;
D(0,3) = 0.0;
D(0,4) = 0.0;
D(1,0) = y[2];
D(1,1) = y[3];
D(1,2) = y[0];
D(1,3) = y[1];
D(1,4) = 0.0;
}
}
Output
T Y(0) Y(1) Length
10.0000000 1.0998138 -0.0202353 1.0999999
20.0000000 1.0970403 -0.0806356 1.0999998
30.0000000 1.0852183 -0.1797250 1.0999999
40.0000000 1.0541573 -0.3142486 1.0999999
50.0000000 0.9912723 -0.4768429 1.1000000
Example 3 – User Solves Linear System
Consider the system of ordinary differential equations, yʹ = By, where B is the bi-diagonal matrix with (-1, -1/2, -1/3, ..., -1/(n-1), 0) on the main diagonal and with 1’s along the first sub-diagonal. The initial condition is y(0) = (1,0,0,...,0)T, and since yʹ (0) = By(0) = (-1,1,0,...,0) T, yʹ (0) is also known for this problem.
Since B T v = 0, where vi = 1/(i-1)!, v is an eigenvector of B T corresponding to the eigenvalue 0. Thus
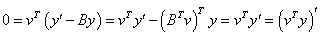
so v T y(t) is constant. Since it has the value v T y(0) = v1 = 1 at t = 0, the constraint v T y(t) = 1 is satisfied for all t. This constraint is imposed in this example.
This example also illustrates how the user can solve his/her own linear systems (matstr=2). Normally, when ires = 6, the matrix
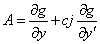
is computed, saved and possibly factored, using a sparse matrix factorization function of the user’s choice. Then when ires=7, the system Ax = delta is solved, using the matrix B saved and factored earlier, and the solution is returned in delta. In this case, B is just a bidiagonal matrix, so there is no need to save or factor A when ires = 6, since a bi-diagonal system can be solved directly using forward substitution, when ires = 7.
#include <imsl.h>
#include <math.h>
#include <stdio.h>
#define NEQ 100
void gcn(int neq, float t, float y[], float yprime[], float delta[],
float *d, int ldd, int *ires);
int main() {
int i, ido, nsteps=10, ncon=1, iypr=0, matstr=2;
float atol[NEQ], con=0.0, t, tend, v[NEQ], y[NEQ], yprime[NEQ];
/* a^t eigenvector v */
v[0] = 1.0;
for (i = 1; i < NEQ; i++)
v[i] = v[i-1] / (float) i;
/* initial values */
for (i = 0; i < NEQ; i++) {
y[i] = 0.0;
yprime[i] = 0.0;
atol[i] = 1.0e-4;
}
y[0] = 1.0;
yprime[0] = -1.0;
yprime[1] = 1.0;
/* always set ido=1 on first call */
ido = 1;
for (i = 0; i < nsteps; i++) {
/* output solution at t=1,2,...,10 */
t = (float) i;
tend = (float) (i + 1);
/* set ido = 3 on last call */
if (i == (nsteps-1))
ido = 3;
/* user-defined jacobian matrix structure (matstr=2) */
imsl_f_differential_algebraic_eqs(NEQ, &t, tend, &ido, y,
yprime, gcn,
IMSL_N_CONSTRAINTS, ncon,
IMSL_YPRIME_METHOD, iypr,
IMSL_JACOBIAN_MATRIX_TYPE, matstr,
IMSL_ABSOLUTE_TOLERANCE, atol,
0);
}
/* check if solution satisfies constraint */
for (i = 0; i < NEQ; i++)
con += v[i] * y[i];
printf(" V dot Y = %f\n", con);
}
void gcn(int neq, float t, float y[], float yprime[], float delta[],
float *d, int ldd, int *ires)
{
#define D(I_,J_) (*(d+(I_)*(neq)+(J_)))
int i;
float con, v[NEQ];
static float cj;
v[0] = 1.0;
for (i = 1; i < NEQ; i++)
v[i] = v[i-1] / (float) i;
if (*ires == 1) {
/* f_i defined here */
delta[0] = yprime[0] + y[0];
for (i = 1; i < (NEQ - 1); i++)
delta[i] = yprime[i] - y[i-1] + y[i] / (float) (i + 1);
delta[NEQ-1] = yprime[NEQ-1] - y[NEQ-2];
} else if (*ires == 5) {
/* constraint is v dot y = 1 */
con = -1.0;
for (i = 0; i < NEQ; i++) {
con += v[i]*y[i];
D(0,i) = v[i];
}
delta[0] = con;
} else if (*ires == 6) {
/* normally, compute matrix
a = df/dy + cj*df/dy' = -b + cj*i
here. only cj needs to be saved in this case, however,
since b is bidiagonal, so a*x=delta can be solved (ires=7)
without saving or factoring b. */
cj = delta[0];
/* if cj > 0 not close to zero, a is nonsingular,
so set ires = 0. */
if (cj >= 1.0e-4)
*ires = 0;
} else if (*ires == 7) {
/* solve a*x=delta and return x in delta. */
delta[0] /= 1.0 + cj;
for (i = 1; i < (NEQ - 1); i++)
delta[i] = (delta[i] + delta[i-1]) /
(1.0 / (float) (i + 1) + cj);
delta[NEQ-1] = (delta[NEQ-1] + delta[NEQ-2]) / cj;
}
}
Output
V dot Y = 1.000000
Fatal Errors
|
IMSL_SYSTEM_CONVERGENCE |
The system has index # but convergence of “yprime” values was not achieved. |
|
IMSL_SYSTEM_CONVERGENCE |
The system appears to have index > 1. |
|
IMSL_SYS_INDEX_GT_ONE |
For the Pareto distribution, the Hessian cannot be calculated because the parameter estimate is 0. |
|
IMSL_SYS_NOT_DIFF_ALG |
This is not a differential-algebraic system. |
|
IMSL_ACCURACY_EXCEEDED_1 |
Accuracy requested exceeds machine precision. |
|
IMSL_STEPS_EXCEEDED |
More than “maxsteps”=# steps taken between output points. |
|
IMSL_ERROR_TEST_FAILURE_2 |
The error test has failed repeatedly. |
|
IMSL_CORRECTOR_FAILED_3 |
The corrector iteration failed repeatedly to converge. |
|
IMSL_SINGULAR_MATRIX_1 |
The iteration matrix is singular. |
|
IMSL_UNABLE_TO_SOLVE_YPR |
Unable to solve for initial “yprime”. |
|
IMSL_TEND_GT_TSTOP |
“tend” is greater than “tstop”. |
|
IMSL_TEND_CLOSE_TO_T |
“tend” is too close to “t”. |
|
IMSL_TSTOP_INCONSIST_T |
“tstop” is not consistent with“t”. |
|
IMSL_CONSTRAINTS_INCONSIST |
Constraints appear inconsistent |
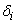
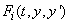
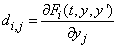 ,
,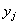
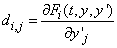 ,
,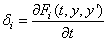 ,
,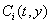
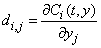 ,
,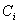
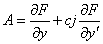 ,
,