Solves a stiff initial-value problem for ordinary differential equations using the Adams-Gear methods.
Synopsis
#include <imsl.h>
float imsl_f_ode_adams_gear_mgr (int task, void **state, …, 0)
void imsl_f_ode_adams_gear (int neq, float *t, float tend, float y[], void *state, void fcn())
The type double functions are imsl_d_ode_adams_gear_mgr and imsl_d_ode_adams_gear.
Required Arguments for imsl_f_ode_adams_gear_mgr
int task
(Input)
This function must be called with task set to IMSL_ODE_INITIALIZE to
set up for solving an ODE system and with task equal to IMSL_ODE_RESET to
clean up after it has been solved. These values for task are defined in
the included file, imsl.h.
void **state
(Input/Output)
The current state of the ODE solution is held in a structure
pointed to by state. It cannot be
directly manipulated.
Required Arguments for imsl_f_ode_adams_gear
int neq
(Input)
Number of differential equations.
float *t
(Input/Output)
Independent variable. On input, t is the initial
independent variable value. On output, t is replaced by tend unless error
conditions arise.
float tend
(Input)
Value of t at which the
solution is desired. The value tend may be less than
the initial value of t.
float y[]
(Input/Output)
Array with neq components
containing a vector of dependent variables. On input, y contains the initial
values. On output, y contains the
approximate solution.
void *state
(Input/Output)
The current state of the ODE solution is held in a structure
pointed to by state. It must be
initialized by a call to imsl_f_ode_adams_gear_mgr.
It cannot be directly manipulated.
void fcn(int neq, float t, float *y, float *yprime)
User-supplied
function to evaluate the right-hand side where
float
*yprime (Output)
Array with neq components containing the vector y′. This function computes
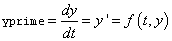
and neq, t, and *y are defined immediately preceding this function.
Synopsis with Optional Arguments
#include <imsl.h>
float imsl_f_ode_adams_gear_mgr (int task, void **state,
IMSL_JACOBIAN, void fcnj(),
IMSL_METHOD, int method,
IMSL_MAXORD, int maxord,
IMSL_MITER, int miter,
IMSL_TOL, float tol,
IMSL_HINIT, float hinit,
IMSL_HMIN, float hmin,
IMSL_HMAX, float hmax,
IMSL_MAX_NUMBER_STEPS, int max_steps,
IMSL_MAX_NUMBER_FCN_EVALS, int max_fcn_evals,
IMSL_SCALE, float scale,
IMSL_NORM, int norm,
IMSL_FLOOR, float floor,
IMSL_NSTEP, int *nstep,
IMSL_NFCN, int *nfcn,
IMSL_NFCNJ, int *nfcnj,
IMSL_FCN_W_DATA, void fcn(), void *data,
IMSL_JACOBIAN_W_DATA, void fcn(), void *data,
0)
Optional Arguments
IMSL_JACOBIAN, void fcnj
(int neq, float t, float *y, float yprime[],
float dypdy[])…(Input)
User-supplied
function to evaluate the Jacobian matrix.
int neq
(Input)
Number of differential equations.
float *t
(Input)
Independent variable. On input, t is the initial
independent variable value. On output, t is replaced by tend unless error
conditions arise.
float *y
(Input)
Array with neq components
containing a vector of dependent variables. On input, y contains the initial
values. On output, y contains the
approximate solution.
float yprime[]
(Input)
Array with neq components
containing the vector y′ = f(t,
y).
float dypdy[]
(Output)
Array of size neq × neq containing the
partial derivatives. Each derivative ∂fi ∕ ∂yj is evaluated at
the provided (t, y) values and is returned in array location
dypdy[(i − 1)*n + j − 1]. And neq, t, and *y are described in the “Required Arguments” section.
IMSL_METHOD, int method
(Input)
Choose the class of integration methods.
1 — Use implicit Adams
method.
2 — Use backward differentiation formula (BDF) methods.
Default:
method = 2
IMSL_MAXORD, int maxord
(Input)
Define the highest order formula to use of implicit Adams type or BDF
type. The default is the value 12 for Adams formulas and is the value 5
for BDF formulas.
IMSL_MITER, int miter
(Input)
Choose the method for solving the formula equations.
1 — Use a
function iteration or successive substitution.
Note: If the problem is
stiff and a chord or modified Newton method is most efficient, use MITER = 2 or = 3.
2 — Use a chord or modified Newton method and a user-supplied Jacobian matrix.
3 — Same as 2 except Jacobian is approximated within the function by divided differences.
4 — Use a
chord method with the Jacobian replaced by a diagonal matrix based on a
directional directive.
Default: miter = 3
IMSL_TOL, float tol
(Input)
Tolerance for error control. An attempt is made to control the norm
of the local error such that the global error is proportional to tol.
Default: tol = 0.001
IMSL_HINIT, float hinit
(Input)
Initial value for the step size h. Steps are applied in the
direction of integration.
Default: hinit = 0.001|tend − t|.
IMSL_HMIN, float hmin
(Input)
Minimum value for the step size h.
Default: hmin = 0.0.
IMSL_HMAX, float hmax
(Input)
Maximum value for the step size h.
Default: hmax = imsl_amach(2).
IMSL_MAX_NUMBER_STEPS, int max_steps
(Input)
Maximum number of steps allowed.
Default: max_steps = 500.
IMSL_MAX_NUMBER_FCN_EVALS, int max_fcn_evals
(Input)
Maximum number of evaluations of y′ allowed.
Default:
max_fcn_evals = No enforced limit.
IMSL_SCALE, float scale
(Input)
A measure of the scale of the problem, such as an approximation to
the Jacobian along the trajectory.
Default: scale = 1.0.
IMSL_NORM, int norm
(Input)
Switch determining the error norm. In the following, ei is the absolute
value of the error estimate for yi(t).
0 — minimum of the absolute error and the relative error, equals the maximum of ei ∕ (max (|yi(t)|, 1.0)) for i = 1, …, neq.
1 — absolute error, equals maxiei.
2 — maxi (ei ∕ wi)where wi = max (|yi(t)|, floor). The value of floor is reset using IMSL_FLOOR.
3 — Scaled Euclidean norm defined as

Where wi = (max(|yi(t)|, 1.0).
Default:
norm = 0.
IMSL_FLOOR, float floor
(Input)
This is used with IMSL_NORM. It provides
a positive lower bound for the error norm option with value 2.
Default: floor = 1.0.
IMSL_NSTEP, int *nstep
(Output)
Returns the number of steps taken.
IMSL_NFCN, int *nfcn
(Output)
Returns the number of evaluations of y′
used.
IMSL_NFCNJ, int *nfcnj
(Output)
Returns the number of Jacobian matrix evaluations used. This value
will be nonzero only if the option IMSL_JACOBIAN is
used.
IMSL_FCN_W_DATA,
void fcn (int neq, float t, float *y, float *yprime, void *data),
void *data,
(Input)
User-supplied function to evaluate the right-hand side, which also
accepts a pointer to data that is supplied by the user. data is a pointer to the
data to be passed to the user-supplied function. See the Introduction, Passing Data to
User-Supplied Functions at the beginning of this manual for more
details.
IMSL_JACOBIAN_W_DATA,
void jacobian
(int neq, float t, float *y, float yprime[],
float dypdy[], void *data),
void *data
(Input)
User supplied function to compute the Jacobian, which also accepts a
pointer to data that is supplied by the user. data is a pointer to
the data to be passed to the user-supplied function. See the Introduction, Passing Data to
User-Supplied Functions at the beginning of this manual for more
details.
Description
The function imsl_f_ode_adams_gear finds an approximation to the solution of a system of first-order differential equations of the form
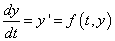
with given initial conditions for y at the starting value for t. The function attempts to keep the global error proportional to a user-specified tolerance. The proportionality depends on the differential equation and the range of integration.
The code is based on using backward difference formulas not exceeding order five as outlined in Gear (1971) and implemented by Hindmarsh (1974). There is an optional use of the code that employs implicit Adams formulas. This use is intended for nonstiff problems with expensive functions y′ = ƒ(t, y).
Examples
Example 1
This is a mildly stiff example problem (F2) from the test set of Enright and Pryce (1987):
|
y′1 |
= |
−y1 − y1y2 + k1y2 |
|
y′2 |
= |
−k2y2 + k3 (1 − y2) y1 |
|
y1 (0) |
= |
1 |
|
y2 (0) |
= |
0 |
|
k1 |
= |
294. |
|
k2 |
= |
3. |
|
k3 |
= |
0.01020408 |
|
tend |
= |
240. |
The ODE solver is initialized by a call to imsl_f_ode_adams_gear_mgr with IMSL_ODE_INITIALIZE. This is the simplest use of the solver, so none of the default values are changed. The function imsl_f_ode_adams_gear is then called to integrate from t = 0 to t = 240.
#include <stdio.h>
#include <imsl.h>
void fcn (int neq, float t, float y[], float yprime[]);
float k1 = 294.0; /* Model data */
float k2 = 3.0;
float k3 = 0.01020408;
int main()
{
int neq = 2; /* Number of ode’s */
float t = 0.0; /* Initial time */
float tend = 240.0; /* Final time */
float y[2] = {1.0, 0.0}; /* Initial condition */
void *state;
/* Initialize the ODE solver */
imsl_f_ode_adams_gear_mgr(IMSL_ODE_INITIALIZE, &state, 0);
/* Integrate from t=0 to tend=240 */
imsl_f_ode_adams_gear (neq, &t, tend, y, state, fcn);
/* Print the solution */
printf("y[%f] = %f, %f\n", t, y[0], y[1]);
}
void fcn (int neq, float t, float y[], float yprime[])
{
yprime[0] = -y[0] - y[0]*y[1] + k1*y[1];
yprime[1] = -k2*y[1] + k3*(1.0-y[1])*y[0];
}
Output
y[240.000000] = 0.392391, 0.001334
Example 2
This problem is a stiff example (F5) from the test set of Enright and Pryce (1987). An initial step size of h = 10-7 is suggested by these authors. It is necessary to provide for more evaluations of y′ and for more steps than the default value allows. Both have been set to 4000.
|
y′1 |
= |
k1 (− k2y1y2 + k3y4 − k4y1y3) |
|
y′2 |
= |
−k1k2y1y2 + k5y4 |
|
y′3 |
= |
k1 (−k4y1y3 + k6y4) |
|
y′4 |
= |
k1 (k2y1y2 − k3y4 + k4y1y3) |
|
y1(0) |
= |
3.365 × 10-7 |
|
y2(0) |
= |
8.261 × 10-3 |
|
y3(0) |
= |
1.641 × 10-3 |
|
y4(0) |
= |
9.380 × 10-6 |
|
k1 |
= |
1011 |
|
k2 |
= |
3. |
|
k3 |
= |
0.0012 |
|
k4 |
= |
9. |
|
k5 |
= |
2 × 107 |
|
k6 |
= |
0.001 |
|
tend |
= |
100. |
The last call to imsl_f_ode_adams_gear_mgr with IMSL_ODE_RESET releases workspace.
#include <stdio.h>
#include <imsl.h>
void fcn (int neq, float t, float y[], float yprime[]);
float k1 = 1.e11; /* Model data */
float k2 = 3.0;
float k3 = 0.0012;
float k4 = 9.0;
float k5 = 2.e7;
float k6 = 0.001;
int main()
{
int neq = 4; /* Number of ode’s */
float t = 0.0; /* Initial time */
float tend = 100.0; /* Final time */
/* Initial condition */
float y[4] = {3.365e-7, 8.261e-3, 1.642e-3, 9.380e-6};
void *state;
int int nfcn;
/* Initialize the ODE solver */
imsl_f_ode_adams_gear_mgr(IMSL_ODE_INITIALIZE, &state,
IMSL_HINIT, 1.e-7,
IMSL_MAX_NUMBER_STEPS, 4000,
IMSL_MAX_NUMBER_FCN_EVALS, 4000,
IMSL_NFCN, &nfcn,
0);
/* Integrate from t=0 to tend=100 */
imsl_f_ode_adams_gear (neq, &t, tend, y, state, fcn);
/* Release workspace and reset */
imsl_f_ode_adams_gear_mgr(IMSL_ODE_RESET, &state, 0);
/* Print the solution */
printf("y[%f] = %f, %f, %f, %f\n", t, y[0], y[1], y[2], y[3]);
/* Print the number of evaluations
of yprime[] */
printf("Number of yprime[] evaluations: %d\n", nfcn);
}
void fcn (int neq, float t, float y[], float yprime[])
{
yprime[0] = k1*(-k2*y[0]*y[1]+k3*y[3]-k4*y[0]*y[2]);
yprime[1] = -k1*k2*y[0]*y[1] + k5*y[3];
yprime[2] = k1*(-k4*y[0]*y[2] + k6*y[3]);
yprime[3] = k1*(k2*y[0]*y[1] - k3*y[3] + k4*y[0]*y[2]);
}
Output
y[100.000000] = 0.000000, 0.003352, 0.005586, 0.000009
Number of yprime[] evaluations: 3630
Fatal Errors
IMSL_ODE_TOO_MANY_EVALS Completion of the next step would make the number of function evaluations #, but only # are allowed.
IMSL_ODE_TOO_MANY_STEPS Maximum number of steps allowed, # have been used. Try increasing the maximum number of steps allowed or increase the tolerance.
