Computes forecasts and their associated probability limits for an ARMA model.
Synopsis
#include <imsls.h>
float *imsls_f_arma_forecast (Imsls_f_arma *arma_info, int n_predict, ..., 0)
The type double function is imsls_d_arma_forecast.
Required Arguments
Imsls_f_arma
*arma_info (Input)
Pointer to a structure of type
Imsls_f_arma that is passed from the imsls_f_arma
function.
int n_predict
(Input)
Maximum lead time for forecasts. Argument n_predict must be
greater than 0.
Return Value
Pointer to an array of length n_predict × (backward_origin + 3) containing the forecasts up to n_predict steps ahead and the information necessary to obtain pairwise confidence intervals. More information is given in the description of argument IMSLS_RETURN_USER.
Synopsis with Optional Arguments
#include <imsls.h>
float
*imsls_f_arma_forecast (Imsls_f_arma
*arma_info,
int n_predict,
IMSLS_CONFIDENCE,
float
confidence,
IMSLS_BACKWARD_ORIGIN,
int
backward_origin,
IMSLS_ONE_STEP_FORECAST,
float
**forecast,
IMSLS_ONE_STEP_FORECAST_USER,
float
forecast[],
IMSLS_RETURN_USER,
float
forecasts[],
0)
Optional Arguments
IMSLS_CONFIDENCE, float
confidence (Input)
Value in the exclusive interval (0,
100) used to specify the confidence percent
probability limits of the forecasts. Typical choices for confidence are 90.0,
95.0, and 99.0.
Default: confidence = 95.0.
IMSLS_BACKWARD_ORIGIN, int
backward_origin (Input)
If specified, the maximum backward
origin. Argument backward_origin must be greater than or equal to 0 and less
than or equal to n_observations − max
(maxar, maxma), where maxar = max (ar_lags [i]),
maxma = max (ma_lags [j]),
and n_observations = the
number of observations in the series, as input in function imsls_f_arma. n_predict forecasts
beginning at origins n_observations − backward_origin +1
through n_observations are
generated.
Default: backward_origin =
0.
IMSLS_ONE_STEP_FORECAST, float
**forecast (Output)
Address of a pointer to an internally
allocated array of length backward_origin + n_predict containing
forecasts. The first backward_origin
forecasts are one-step ahead forecasts for the last backward_origin values
in the series. The next n_predict values in
the returned series are forecasts for the next values beyond the series.
IMSLS_ONE_STEP_FORECAST_USER, float
forecast[] (Output)
Storage
for array forecast is provided by the user. See IMSLS_ONE_STEP_FORECAST.
IMSLS_RETURN_USER, float
forecasts[] (Output)
If specified, a user-specified array
of length
n_predict × (backward_origin + 3)
as defined below.
|
Column |
Content |
|
j |
forecasts for lead times l = 1, ..., n_predict at origins n_observations − backward_origin + 1+ j, where j = 0, ..., backward_origin |
|
backward_origin + 1 |
deviations from each forecast that give the confidence percent probability limits |
|
backward_origin + 2 |
psi weights of the infinite order moving average form of the model |
Also see Examples for additional explanation of how to interpret this output.
Description
The Box-Jenkins forecasts and their associated probability limits for a nonseasonal ARMA model are computed given a sample of n = n_observations {Zt} for t = 1, 2, ..., n, where n_observations = the number of observations in the series, as input in function imsls_f_arma.
Suppose the time series {Zt} is generated by a nonseasonal ARMA model of the form
φ(B)Zt = θ0 + θ(B)At
for t ∈ {0, ±1, ±2, ...}, where B is the backward shift operator, θ0 is the constant, and
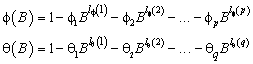
with p autoregressive and q moving average parameters. Without loss of generality, the following is assumed:
1 ≤ lφ (1) ≤ lφ (2) ≤ … ≤ lφ (p)
1 ≤ lθ (1) ≤ lθ (2) ≤ … ≤ lθ (q)
so that the nonseasonal ARMA model is of order (pʹ, qʹ), where pʹ = lφ(p) and qʹ = lθ(q). Note that the usual hierarchical model assumes the following:
lφ (i) = i, 1 ≤ i ≤ p
lθ (j) = j, 1 ≤ j ≤ q
The Box-Jenkins forecast at origin t for lead time l of Zt+l is defined in terms of the difference equation
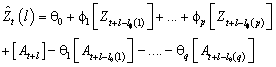
where the following is true:
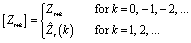
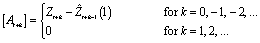
The 100(1 − α) percent probability limits for Zt+l are given by
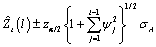
where z(a/2) is the 100(1 − α/2) percentile of the standard normal distribution
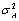
(returned from imsls_f_arma) and
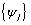
are the parameters of the random shock form of the difference equation. Note that the forecasts are computed for lead times l = 1, 2, ..., L at origins t = (n − b), (n − b + 1), ..., n, where L = n_predict and b = backward_origin.
The Box-Jenkins forecasts minimize the mean-square error
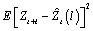
Also, the forecasts can be easily updated according to the following equation:
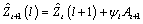
This approach and others are discussed in Chapter 5: “Forecasting” of Box and Jenkins (1976).
Examples
Example 1
Consider the Wolfer Sunspot Data (Anderson 1971, p. 660)
consisting of the number of sunspots observed each year from 1749 through 1924.
The data set for this example consists of the number of sunspots observed from
1770 through 1869. Function imsls_f_arma_forecast
computes forecasts and 95-percent probability limits for the forecasts for an
ARMA(2, 1) model fit using function imsls_f_arma
with the method of moments option. With backward_origin
= 3, columns zero through three of forecasts
provide forecasts starting with 1867, 1868, 1869, and 1870, respectively. Note
that the values in the first row are the one-step ahead forecasts for 1867,
1868, 1869, and 1870; the values in the second row are the two-step ahead
forecasts for 1868, 1869, 1870, and 1871; etc. Column four gives the deviations
for computing probability limits, and column five gives the psi weights, which
can be used to update forecasts when more data is available. For example, the
forecast for the 102nd observation (year 1871) given the data through the 100th
observation (year 1869) is 77.21; and 95-percent probability limits are given by
77.21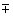
56.30. After observation 101 (
Z101 for year 1870) is
available, the forecast can be updated by using
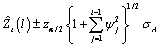
with the psi weight (ψ1 = 1.37) and the one-step-ahead forecast error for observation 101 (Z101 − 83.72) to give the following:
77.21 + 1.37 × (Z101 − 83.72)
Since this updated forecast is one step ahead, the
95-percent probability limits are now given by the forecast 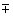33.22.
#include <imsls.h>
#include <stdio.h>
int main()
{
int p=2, q=1, i, n_observations=100, max_iterations=0;
float w[176][2], z[100], *parameters, relative_error=0.0;
imsls_f_data_sets(2, IMSLS_X_COL_DIM,
2, IMSLS_RETURN_USER, w,
0);
for (i=0; i<n_observations; i++) z[i] = w[21+i][1];
parameters = imsls_f_arma(n_observations, &z[0], p, q,
IMSLS_RELATIVE_ERROR, relative_error,
IMSLS_MAX_ITERATIONS, max_iterations,
0);
printf("AR estimates are %11.4f and %11.4f.\n",
parameters[1], parameters[2]);
printf("MA estimate is %11.4f.\n", parameters[3]);
}
Output
Method of Moments initial estimates:
AR estimates are 1.2443 and -0.5751.
MA estimate is -0.1241.
* * * Forecast Table * * *
Lead Time Forecast From Forecast From Forecast From Forecast From
1866 1867 1868 1869
1 18.2833 16.6151 55.1893 83.7196
2 28.9182 32.0189 62.7606 77.2092
3 41.0101 45.8275 61.8922 63.4608
4 49.9387 54.1496 56.4571 50.0987
5 54.0937 56.5623 50.1939 41.3803
6 54.1282 54.7780 45.5268 38.2174
7 51.7815 51.1701 43.3221 39.2965
8 48.8417 47.7072 43.2631 42.4582
9 46.5335 45.4736 44.4577 45.7715
10 45.3524 44.6861 45.9781 48.0758
11 45.2103 44.9909 47.1827 49.0371
12 45.7128 45.8230 47.8072 48.9080
Lead Time Dev. for Prob. Psi
Limits
1 33.2179 1.3684
2 56.2980 1.1274
3 67.6168 0.6158
4 70.6432 0.1178
5 70.7515 -0.2076
6 71.0869 -0.3261
7 71.9074 -0.2863
8 72.5337 -0.1687
9 72.7498 -0.0452
10 72.7653 0.0407
11 72.7779 0.0767
12 72.8225 0.0720
Example 2
Using the same data as in example 1, option IMSLS_ONE_STEP_FORECAST
is used to compute the one-step ahead forecasts with backward_origin = 0
and n_predict = 5. This obtains
the one-step ahead forecasts for the last 10 observations in the series, i.e.
years 1860-1869, plus the next 5 years. The upper 90% confidence limits
are computed for these forecasts using the deviations in column backward_origin +1
of forecasts.
#include <imsls.h>
#include <stdio.h>
int main()
{
int p=2, q=1, i, n_observations=100;
float w[176][2], z[100], *parameters;
imsls_f_data_sets(2, IMSLS_X_COL_DIM,
2, IMSLS_RETURN_USER, w,
0);
for (i=0; i<n_observations; i++) z[i] = w[21+i][1];
parameters = imsls_f_arma(n_observations, &z[0], p, q,
IMSLS_LEAST_SQUARES,
0);
printf("AR estimates are %11.4f and %11.4f.\n",
parameters[1], parameters[2]);
printf("MA estimate is %11.4f.\n", parameters[3]);
}
Output
ARMA ONE-STEP AHEAD FORECASTS
Year Observed Forecast Residual UCL(90%)
1860 95.700 100.737 -5.037 128.615
1861 77.200 81.295 -4.095 109.173
1862 59.100 57.067 2.033 84.944
1863 44.000 44.426 -0.426 72.303
1864 47.000 36.353 10.647 64.230
1865 30.500 47.396 -16.896 75.274
1866 16.300 28.558 -12.258 56.436
1867 7.300 19.804 -12.504 47.682
1868 37.300 16.804 20.496 44.681
1869 73.900 55.213 18.687 83.090
1870 - 83.723 - 111.600
1871 - 77.213 - 124.460
1872 - 63.464 - 120.210
1873 - 50.100 - 109.386
1874 - 41.380 - 100.757
