Automatically identifies time
series outliers, determines parameters of a multiplicative seasonal ARIMA model and produces forecasts
that incorporate the effects of outliers whose effects persist beyond the end of
the series.
model and produces forecasts
that incorporate the effects of outliers whose effects persist beyond the end of
the series.
Synopsis
#include <imsls.h>
float *imsls_f_auto_arima (int n_obs, int tpoints[], float x[],...,0)
The type double function is imsls_d_auto_arima.
Required Arguments
int n_obs
(Input)
Number of observations in the original time series. Assuming
that the series is defined at time points  , the actual length of the series,
including missing observations is
, the actual length of the series,
including missing observations is  .
.
int tpoints[]
(Input)
A vector of length n_obs containing the
time points 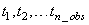 the time series was observed.
It is required that
the time series was observed.
It is required that 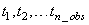 are in strictly
ascending order.
are in strictly
ascending order.
float x[] (Input)
A
vector of length n_obs containing the
observed time series values 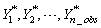 . This series can
contain outliers and missing observations. Outliers are identified by this
function and missing values are identified by the time values in vector tpoints. If the time
interval between two consecutive time points is greater than one, i.e.
. This series can
contain outliers and missing observations. Outliers are identified by this
function and missing values are identified by the time values in vector tpoints. If the time
interval between two consecutive time points is greater than one, i.e.
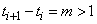 , then
, then  missing values are assumed to
exist between
missing values are assumed to
exist between 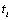 and
and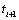 at times
at times  . Therefore, the gap free series is
assumed to be defined for equidistant time points . Missing values are
automatically estimated prior to identifying outliers and producing
forecasts. Forecasts are generated for both missing and observed
values.
. Therefore, the gap free series is
assumed to be defined for equidistant time points . Missing values are
automatically estimated prior to identifying outliers and producing
forecasts. Forecasts are generated for both missing and observed
values.
Return Value
Pointer to an array of length 1 + p + q with the
estimated constant, AR and MA parameters used to fit the outlier-free series
using an ARIMA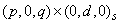 model. Upon
completion, if d=model[3]=0,
then an ARMA(p, q) model or AR(p) model is fitted to the
outlier-free version of the observed series
model. Upon
completion, if d=model[3]=0,
then an ARMA(p, q) model or AR(p) model is fitted to the
outlier-free version of the observed series 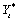 . If d=model[3]>0,
these parameters are computed for an ARMA(p,q) representation of
the seasonally adjusted series
. If d=model[3]>0,
these parameters are computed for an ARMA(p,q) representation of
the seasonally adjusted series  , where
, where 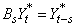 and s=model[2]≥1.
and s=model[2]≥1.
If an error occurred, NULL is returned.
Synopsis with Optional Arguments
#include <imsls.h>
float
*imsls_f_auto_arima (int
n_obs,
int tpoints[],
float x[],
IMSLS_RETURN_USER,
float parameters[],
IMSLS_METHOD, int
method,
IMSLS_MAX_LAG, int
maxlag,
IMSLS_MODEL, int
model[],
IMSLS_DELTA,
float delta,
IMSLS_CRITICAL,
float critical,
IMSLS_EPSILON, float
epsilon,
IMSLS_RESIDUAL, float
**residual,
IMSLS_RESIDUAL_USER,
float residual[],
IMSLS_RESIDUAL_SIGMA,
float *res_sigma,
IMSLS_NUM_OUTLIERS,
int *num_outliers,
IMSLS_P_INITIAL, int
n_p_initial,
int p_initial[],
IMSLS_Q_INITIAL, int
n_q_initial,
int q_initial[],
IMSLS_S_INITIAL,
int n_s_initial,
int s_initial[],
IMSLS_D_INITIAL,
int n_d_initial,
int d_initial[],
IMSLS_OUTLIER_STATISTICS,
int **outlier_stat,
IMSLS_OUTLIER_STATISTICS_USER,
int outlier_stat[],
IMSLS_AIC,
float *aic,
IMSLS_AICC,
float *aicc,
IMSLS_BIC,
float *bic,
IMSLS_MODEL_SELECTION_CRITERION,
int criterion,
IMSLS_OUT_FREE_SERIES,
float **outfree_series,
IMSLS_OUT_FREE_SERIES_USER,
float outfree_series[],
IMSLS_CONFIDENCE,
float confidence,
IMSLS_NUM_PREDICT, int
n_predict,
IMSLS_OUT_FREE_FORECAST,
float **outfree_forecast,
IMSLS_OUT_FREE_FORECAST_USER,
float outfree_forecast[],
IMSLS_OUTLIER_FORECAST,
float **outlier_forecast,
IMSLS_OUTLIER_FORECAST_USER,
float outlier_forecast[],
0)
Optional Arguments
IMSLS_METHOD, int method
(Input)
The method used in model selection:
1 — Automatic
ARIMA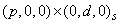 selection
selection
2 —
Grid search
Requires arguments IMSLS_P_INITIAL and
IMSLS_Q_INITIAL.
3 — Specified
ARIMA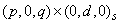 model
model
Requires
argument IMSLS_MODEL.
Default: method = 1
For more
information, see the Description section.
IMSLS_MAX_LAG, int maxlag (Input)
The maximum lag
allowed when fitting an AR(p) model.
Default: maxlag = 10
IMSLS_MODEL, int model[]
(Input/Output)
Array of length 4
containing the values for p, q, s, d. If method=3 is chosen,
then the values for p and q must be defined. If IMSLS_S_INITIAL and
IMSLS_D_INITIAL
are not defined, then also s and d must be given. If method=1 or method=2, then model
is ignored as an input array. On output, model contains the optimum values
for p, q, s, d in model[0], model[1], model[2] and model[3],
respectively.
IMSLS_DELTA, float delta (Input)
The
dampening effect parameter used in the detection of a Temporary Change Outlier
(TC), 0<delta<1.
Default: delta =
0.7
IMSLS_CRITICAL, float critical
(Input)
Critical value
used as a threshold for outlier detection, critical >
0.
Default: critical
= 3.0
IMSLS_EPSILON, float epsilon
(Input)
Positive tolerance value controlling the
accuracy of parameter estimates during outlier detection.
Default: epsilon = 0.001
IMSLS_RESIDUAL, float **residual
(Output)
Address of a
pointer to an internally allocated array of length 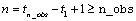 , containing
, containing 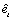 , the estimates of the white noise in
the outlier free original series.
, the estimates of the white noise in
the outlier free original series.
IMSLS_RESIDUAL_USER, float residual[]
(Output)
Storage for array
residual is
provided by the user. See IMSLS_RESIDUAL.
IMSLS_RESIDUAL_SIGMA, float *res_sigma (Output)
Residual standard
error (RSE) of the outlier free original series.
IMSLS_NUM_OUTLIERS, int *num_outliers
(Output)
The number of
outliers detected.
IMSLS_P_INITIAL, int n_p_initial, int p_initial[]
(Input)
An array with
n_p_initial
elements containing the candidate values for p, from which the optimum is
being selected. All candidate values in p_initial[] must be
non-negative and n_p_initial ≥ 1. If
method=2, then
IMSLS_P_INITIAL
must be defined. Otherwise, n_p_initial and p_initial are
ignored.
IMSLS_Q_INITIAL, int n_q_initial, int q_initial[]
(Input)
An array with
n_q_initial
elements containing the candidate values for q, from which the optimum is
being selected. All candidate values in q_initial[] must be
non-negative and n_q_initial ≥ 1. If
method=2, then
IMSLS_Q_INITIAL
must be defined. Otherwise, n_q_initial and q_initial are
ignored.
IMSLS_S_INITIAL, int n_s_initial, int s_initial[]
(Input)
A vector of length
n_s_initial
containing the candidate values for s, from which the
optimum is being selected. All candidate values in s_initial[] must be
positive and n_s_initial ≥ 1.
Default: n_s_initial=1, s_initial={1}
IMSLS_D_INITIAL, int n_d_initial, int d_initial[]
(Input)
A vector of length n_d_initial containing
the candidate values for d, from which the optimum is being
selected. All candidate values in d_initial[] must be
non-negative and n_d_initial ≥
1.
Default: n_d_initial=1, d_initial={0}
IMSLS_OUTLIER_STATISTICS,
int **outlier_stat
(Output)
Address of a
pointer to an internally allocated array of length num_outliers by 2
containing outlier statistics. The first column contains the time at which
the outlier was observed (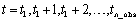 ) and the second column
contains an identifier indicating the type of outlier observed. Outlier
types fall into one of five categories:
) and the second column
contains an identifier indicating the type of outlier observed. Outlier
types fall into one of five categories:
|
0 |
Innovational Outliers (IO) |
|
1 |
Additive Outliers (AO) |
|
2 |
Level Shift Outliers (LS) |
|
3 |
Temporary Change Outliers (TC) |
|
4 |
Unable to Identify (UI). |
If num_outliers=0, NULL is returned.
IMSLS_OUTLIER_STATISTICS_USER,
int outlier_stat[]
(Output)
A user allocated
array of length n × 2 containing outlier
statistics in its first num_outliers rows.
Here,  .
.
See IMSLS_OUTLIER_STATISTICS.
If
num_outliers =
0, outlier_stat
stays unchanged.
IMSLS_AIC, float *aic
(Output)
The AIC (Akaike’s Information Criterion ) value for the
optimum model. Uses an approximation of the maximum log-likelihood based on an
estimate of the innovation variance of the series.
IMSLS_AICC,
float
*aicc
(Output)
The AICC (corrected AIC) value for the optimum model. Uses an
approximation of the maximum log-likelihood based on an estimate of the
innovation variance of the series.
IMSLS_BIC,
float
*bic (Output)
The BIC (Bayesian Information Criterion)
value for the optimum model. Uses an approximation of the maximum log-likelihood
based on an estimate of the innovation variance of the series.
IMSLS_MODEL_SELECTION_CRITERION, int criterion (Input)
The information criterion used for optimum model selection.
|
criterion |
selected information criterion |
|
0 |
Akaike’s Information Criterion (AIC) |
|
1 |
Akaike’s Corrected Information Criterion (AICC) |
|
2 |
Bayesian Information Criterion (BIC) |
Default:
criterion = 0.
IMSLS_OUT_FREE_SERIES, float **outfree_series
(Output)
Address of a pointer to an internally allocated array of
length n by 2, where 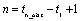 . The first column of
outfree_series
contains the n_obs observations
from the original series,
. The first column of
outfree_series
contains the n_obs observations
from the original series, 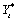 , plus estimated
values for any time gaps. The second column contains the same values as
the first column adjusted by removing any outlier effects. In effect, the second
column contains estimates of the underlying outlier-free series,
, plus estimated
values for any time gaps. The second column contains the same values as
the first column adjusted by removing any outlier effects. In effect, the second
column contains estimates of the underlying outlier-free series, 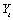 . If no outliers are detected
then both columns will contain identical values.
. If no outliers are detected
then both columns will contain identical values.
IMSLS_OUT_FREE_SERIES_USER,
float outfree_series[]
(Output)
A user allocated array of length n by 2, where 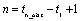 . For further details, see
IMSLS_OUT_FREE_SERIES.
. For further details, see
IMSLS_OUT_FREE_SERIES.
IMSLS_CONFIDENCE, float confidence
(Input)
Confidence level for computing forecast confidence limits,
taken from the exclusive interval (0, 100). Typical choices for confidence are 90.0,
95.0 and 99.0.
Default: confidence = 95.0
IMSLS_NUM_PREDICT, int n_predict
(Input)
The number of forecasts requested. Forecasts are made at
origin  , i.e. from the last observed value
of the series.
, i.e. from the last observed value
of the series.
Default: n_predict = 0
IMSLS_OUT_FREE_FORECAST, float **outfree_forecast
(Output)
Address of a pointer to an internally allocated array of
length n_predict
by 3. The first column contains the forecasted values for the original outlier
free series for t= +1,
+1, 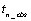 + 2,...,
+ 2,...,  + n_predict. The second
column contains standard errors for these forecasts, and the third column
contains the psi weights of the infinite order moving average form of the
model.
+ n_predict. The second
column contains standard errors for these forecasts, and the third column
contains the psi weights of the infinite order moving average form of the
model.
IMSLS_OUT_FREE_FORECAST_USER,
float outfree_forecast[]
(Output)
A user allocated array of length n_predict by 3. For
more information, see IMSLS_OUT_FREE_FORECAST.
IMSLS_OUTLIER_FORECAST, float **outlier_forecast
(Output)
Address of a pointer to an internally allocated array of
length n_predict
by 3. The first column contains the forecasted values for the original series
for t= +1,
+1,  +2,...,
+2,...,  +n_predict. The second
column contains standard errors for these forecasts, and the third column
contains the
+n_predict. The second
column contains standard errors for these forecasts, and the third column
contains the 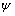 weights of the infinite order moving
average form of the model.
weights of the infinite order moving
average form of the model.
IMSLS_OUTLIER_FORECAST_USER,
float outlier_forecast[]
(Output)
A user allocated array of length n_predict by 3. For
more information, see IMSLS_OUTLIER_FORECAST.
IMSLS_RETURN_USER, float x[]
(Output)
A user allocated array containing the estimated constant,
AR and MA parameters in its first 1+p+q locations. The values p
and q can be estimated by upper bounds: If method=1, an upper
bound for p would be maxlag, and q= 0. If method=2, upper bounds
for p and q would be the maximum values in arrays p_initial and
q_initial,
respectively. If
method=3, p= model[0] and
q= model[1].
Description
Function imsls_f_auto_arima
determines the parameters of a multiplicative seasonal ARIMA model, and then uses the
fitted model to identify outliers and prepare forecasts. The order of this model
can be specified or automatically determined.
model, and then uses the
fitted model to identify outliers and prepare forecasts. The order of this model
can be specified or automatically determined.
The
ARIMA model handled by imsls_f_auto_arima
has the following form:
model handled by imsls_f_auto_arima
has the following form:
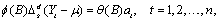
where
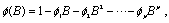
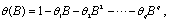
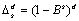
and
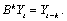
It is assumed that all roots of 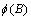 and
and 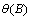 lie outside the unit circle.
Clearly, if
lie outside the unit circle.
Clearly, if 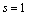 this reduces to the traditional
ARIMA(p, d, q) model.
this reduces to the traditional
ARIMA(p, d, q) model.
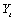 is the unobserved, outlier-free time
series with mean
is the unobserved, outlier-free time
series with mean 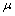 , and white noise
, and white noise 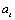 . This model is referred to as the
underlying, outlier-free model. Function
imsls_f_auto_arima
does not assume that this series is observable. It assumes that the observed
values might be contaminated by one or more outliers, whose effects are added to
the underlying outlier-free series:
. This model is referred to as the
underlying, outlier-free model. Function
imsls_f_auto_arima
does not assume that this series is observable. It assumes that the observed
values might be contaminated by one or more outliers, whose effects are added to
the underlying outlier-free series:
Outlier identification uses the algorithm developed by Chen and Liu (1993). Outliers are classified into 1 of 5 types:
1. innovational
2. additive
3. level shift
4. temporary change and
5. unable to identify
Once outliers are identified, imsls_f_auto_arima
estimates 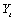 , the outlier-free series
representation of the data, by removing the estimated outlier effects.
, the outlier-free series
representation of the data, by removing the estimated outlier effects.
Using the information about the adjusted ARIMA model and the removed
outliers, forecasts are then prepared for the outlier-free series.
Outlier effects are added to these forecasts to produce a forecast for the
observed series,
model and the removed
outliers, forecasts are then prepared for the outlier-free series.
Outlier effects are added to these forecasts to produce a forecast for the
observed series, 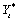 . If there are no outliers,
then the forecasts for the outlier-free series and the observed series will be
identical.
. If there are no outliers,
then the forecasts for the outlier-free series and the observed series will be
identical.
Model Selection
Users have an option of either specifying specific values for p, q , s and d or have imsls_f_auto_arima automatically select best fit values. Model selection can be conducted in one of three methods listed below depending upon the value of variable method.
Method 1: Automatic
ARIMA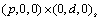 Selection
Selection
This method initially searches for the AR(p) representation with minimum AIC for the noisy data, where p =0,...,maxlag.
If IMSLS_D_INITIAL
is defined then the values in s_initial
and d_initial
are included in the search to find an optimum ARIMA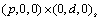 representation of the series.
Here, every possible combination of values for p, s in s_initial
and d in d_initial
is examined. The best found ARIMA
representation of the series.
Here, every possible combination of values for p, s in s_initial
and d in d_initial
is examined. The best found ARIMA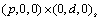 representation is then
used as input for the outlier detection routine.
representation is then
used as input for the outlier detection routine.
The optimum values for p, q, s and d are returned in model[0], model[1], model[2] and model[3], respectively.
Method 2: Grid Search
The second automatic method conducts a grid search for p and q using all possible combinations of candidate values in p_initial and q_initial. Therefore, for this method the definition of IMSLS_P_INITIAL and IMSLS_Q_INITIAL is required.
If IMSLS_D_INITIAL is defined, the grid search is extended to include the candidate values for s and d given in s_initial and d_initial, respectively.
If IMSLS_D_INITIAL is not defined, no seasonal adjustment is attempted, and the grid search is restricted to searching for optimum values of p and q only.
The optimum values of p, q, s and d are returned in model[0], model[1], model[2] and model[3], respectively.
Method 3: Specified
ARIMA Model
Model
In the third method, specific values for p,
q, s and d
are given. The values for p and
q must be defined in model[0] and model[1],
respectively. If IMSLS_S_INITIAL
and IMSLS_D_INITIAL
are not defined, then values  and
and  must be specified in model[2]
and model[3]. If IMSLS_S_INITIAL
and IMSLS_D_INITIAL are defined, then a grid search for the
optimum values of s and
d is conducted using all
possible combinations of input values in s_initial
and d_initial.
The optimum values of s
and d can be found in
model[2]
and model[3],
respectively.
must be specified in model[2]
and model[3]. If IMSLS_S_INITIAL
and IMSLS_D_INITIAL are defined, then a grid search for the
optimum values of s and
d is conducted using all
possible combinations of input values in s_initial
and d_initial.
The optimum values of s
and d can be found in
model[2]
and model[3],
respectively.
Outliers
The algorithm of Chen and Liu (1993) is used to identify outliers. The number of outliers identified is returned in num_outliers. Both the time and classification for these outliers are returned in outlier_stat[]. Outliers are classified into one of five categories based upon the standardized statistic for each outlier type. The time at which the outlier occurred is given in the first column of outlier_stat. The outlier identifier returned in the second column is according to the descriptions in the following table:
|
Outlier Identifier |
Name |
General Description |
|
0 |
(IO) Innovational Outlier |
Innovational outliers persist. That is, there is
an initial impact at the time the outlier occurs. This effect
continues in a lagged fashion with all future observations. The lag
coefficients are determined by the coefficient of the underlying ARIMA
|
|
1 |
(AO) Additive Outlier |
Additive outliers do not persist. As the name implies, an additive outlier effects only the observation at the time the outlier occurs. Hence additive outliers have no effect on future forecasts. |
|
2 |
(LS) |
Level shift outliers persist. They have the effect of either raising or lowering the mean of the series starting at the time the outlier occurs. This shift in the mean is abrupt and permanent. |
|
3 |
(TC) |
Temporary change outliers persist and are similar to level shift outliers with one major exception. Like level shift outliers, there is an abrupt change in the mean of the series at the time this outlier occurs. However, unlike level shift outliers, this shift is not permanent. The TC outlier gradually decays, eventually bringing the mean of the series back to its original value. The rate of this decay is modeled using the parameter delta. The default of delta= 0.7 is the value recommended for general use by Chen and Liu (1993). |
|
4 |
(UI) Unable to Identify |
If an outlier is identified as the last observation, then the algorithm is unable to determine the outlier’s classification. For forecasting, a UI outlier is treated as an IO outlier. That is, its effect is lagged into the forecasts. |
Except for additive outliers (AO), the effect of an outlier persists to observations following that outlier. Forecasts produced by imsls_f_auto_arima take this into account.
Examples
Example 1
This example uses time series D from Box, Jenkins and Reinsel (1994), the hourly viscosity readings of a chemical process. Method 1 without seasonal adjustment is chosen to find an appropriate AR(p) model for the first 304 observations of this series, measured at time points t = 1 to t = 304. A forecast is then done at origin t = 304 for lead times 1 to 6 and compared with the actual time series values which are stored in array actual.
#include <imsls.h>
#include <stdio.h>
int main()
{
int n_obs, n_predict, i, num_outliers;
int *outlier_stat = NULL, model[4], times[304];
float aic, res_sigma, *parameters = NULL;
float outlier_forecast[18], forecast_table[24];
/* Values of series D at time points t=1,...,t=304 */
float x[304] = {
8.0,8.0,7.4,8.0,8.0,8.0,8.0,8.8,8.4,8.4,8.0,8.2,8.2,8.2,8.4,
8.4,8.4,8.6,8.8,8.6,8.6,8.6,8.6,8.6,8.8,8.9,9.1,9.5,8.5,8.4,
8.3,8.2,8.1,8.3,8.4,8.7,8.8,8.8,9.2,9.6,9.0,8.8,8.6,8.6,8.8,
8.8,8.6,8.6,8.4,8.3,8.4,8.3,8.3,8.1,8.2,8.3,8.5,8.1,8.1,7.9,
8.3,8.1,8.1,8.1,8.4,8.7,9.0,9.3,9.3,9.5,9.3,9.5,9.5,9.5,9.5,
9.5,9.5,9.9,9.5,9.7,9.1,9.1,8.9,9.3,9.1,9.1,9.3,9.5,9.3,9.3,
9.3,9.9,9.7,9.1,9.3,9.5,9.4,9.0,9.0,8.8,9.0,8.8,8.6,8.6,8.0,
8.0,8.0,8.0,8.6,8.0,8.0,8.0,7.6,8.6,9.6,9.6,10.0,9.4,9.3,9.2,
9.5,9.5,9.5,9.9,9.9,9.5,9.3,9.5,9.5,9.1,9.3,9.5,9.3,9.1,9.3,
9.1,9.5,9.4,9.5,9.6,10.2,9.8,9.6,9.6,9.4,9.4,9.4,9.4,9.6,9.6,
9.4,9.4,9.0,9.4,9.4,9.6,9.4,9.2,8.8,8.8,9.2,9.2,9.6,9.6,9.8,
9.8,10.0,10.0,9.4,9.8,8.8,8.8,8.8,8.8,9.6,9.6,9.6,9.2,9.2,9.0,
9.0,9.0,9.4,9.0,9.0,9.4,9.4,9.6,9.4,9.6,9.6,9.6,10.0,10.0,9.6,
9.2,9.2,9.2,9.0,9.0,9.6,9.8,10.2,10.0,10.0,10.0,9.4,9.2,9.6,9.7,
9.7,9.8,9.8,9.8,10.0,10.0,8.6,9.0,9.4,9.4,9.4,9.4,9.4,9.6,10.0,
10.0,9.8,9.8,9.7,9.6,9.4,9.2,9.0,9.4,9.6,9.6,9.6,9.6,9.6,9.6,
9.0,9.4,9.4,9.4,9.6,9.4,9.6,9.6,9.8,9.8,9.8,9.6,9.2,9.6,9.2,
9.2,9.6,9.6,9.6,9.6,9.6,9.6,10.0,10.0,10.4,10.4,9.8,9.0,9.6,9.8,
9.6,8.6,8.0,8.0,8.0,8.0,8.4,8.8,8.4,8.4,9.0,9.0,9.4,10.0,10.0,
10.0,10.2,10.0,10.0,9.6,9.0,9.0,8.6,9.0,9.6,9.6,9.0,9.0,8.9,8.8,
8.7,8.6,8.3,7.9};
/* Actual values of series D at time points t=305,...,t=310 */
float actual[6] = {8.5,8.7,8.9,9.1,9.1,9.1};
char *col_labels[] = {
"Lead Time",
"Orig. Series",
"Forecast",
"Dev. for Prob. Limits",
"Psi"};
n_predict = 6;
n_obs = 304;
/* Define times from t=1 to t=304 */
for (i=0;i<n_obs;i++) times[i] = i+1;
parameters = imsls_f_auto_arima(n_obs, times, x,
IMSLS_MODEL, model,
IMSLS_AIC, &aic,
IMSLS_MAX_LAG, 5,
IMSLS_CRITICAL, 3.8,
IMSLS_NUM_OUTLIERS, &num_outliers,
IMSLS_OUTLIER_STATISTICS, &outlier_stat,
IMSLS_RESIDUAL_SIGMA, &res_sigma,
IMSLS_NUM_PREDICT, n_predict,
IMSLS_OUTLIER_FORECAST_USER, outlier_forecast,
0);
printf("\nMethod 1: Automatic ARIMA model selection,"
" no differencing\n");
printf("\nModel chosen: p=%d, q=%d, s=%d, d=%d\n", model[0],
model[1], model[2], model[3]);
printf("\nNumber of outliers: %d\n\n", num_outliers);
printf("Outlier statistics:\n\n");
printf("Time point Outlier type\n");
for (i=0; i<num_outliers; i++)
printf("%d%11d\n", outlier_stat[2*i], outlier_stat[2*i+1]);
printf("\nAIC = %lf\n", aic);
printf("RSE = %lf\n\n", res_sigma);
printf("Parameters:\n");
for (i=0; i<=model[0]+model[1]; i++)
printf("parameters[%d] = %lf\n", i, parameters[i]);
for (i=0; i<n_predict; i++)
{
forecast_table[4*i] = actual[i];
forecast_table[4*i+1] = outlier_forecast[3*i];
forecast_table[4*i+2] = outlier_forecast[3*i+1];
forecast_table[4*i+3] = outlier_forecast[3*i+2];
}
imsls_f_write_matrix("* * * Forecast Table * * *",
n_predict, 4, forecast_table,
IMSLS_COL_LABELS, col_labels,
IMSLS_WRITE_FORMAT, "%11.4f", 0);
}
Output
Method 1: Automatic ARIMA model selection, no differencing
Model chosen: p=1, q=0, s=1, d=0
Number of outliers: 1
Outlier statistics:
Time point Outlier type
217 3
AIC = 678.224731
RSE = 0.290680
Parameters:
parameters[0] = 1.044163
parameters[1] = 0.887724
* * * Forecast Table * * *
Lead Time Orig. Series Forecast Dev. for Prob. Psi
Limits
1 8.5000 8.0572 0.5697 0.8877
2 8.7000 8.1967 0.7618 0.7881
3 8.9000 8.3206 0.8843 0.6996
4 9.1000 8.4306 0.9699 0.6210
5 9.1000 8.5282 1.0325 0.5513
6 9.1000 8.6148 1.0792 0.4894
Example 2
This is the same as Example 1, except now imsls_f_auto_arima
uses Method 2 with a possible seasonal
adjustment. As a result, the unadjusted model with 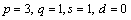 is chosen as optimum.
is chosen as optimum.
#include <imsls.h>
#include <stdio.h>
int main()
{
int n_obs, n_predict, i, num_outliers;
int model[4], times[304];
int n_p_initial = 4, n_q_initial = 4;
int n_s_initial = 2, n_d_initial = 3;
int s_initial[2] = {1,2}, d_initial[3] = {0,1,2};
int p_initial[4] = {0,1,2,3}, q_initial[4] = {0,1,2,3};
int outlier_stat[608];
float aic, res_sigma;
float parameters[7], outlier_forecast[18], forecast_table[24];
/* Values of series D at time points t=1,...,t=304 */
float x[310] = {
8.0,8.0,7.4,8.0,8.0,8.0,8.0,8.8,8.4,8.4,8.0,8.2,8.2,8.2,8.4,
8.4,8.4,8.6,8.8,8.6,8.6,8.6,8.6,8.6,8.8,8.9,9.1,9.5,8.5,8.4,
8.3,8.2,8.1,8.3,8.4,8.7,8.8,8.8,9.2,9.6,9.0,8.8,8.6,8.6,8.8,
8.8,8.6,8.6,8.4,8.3,8.4,8.3,8.3,8.1,8.2,8.3,8.5,8.1,8.1,7.9,
8.3,8.1,8.1,8.1,8.4,8.7,9.0,9.3,9.3,9.5,9.3,9.5,9.5,9.5,9.5,
9.5,9.5,9.9,9.5,9.7,9.1,9.1,8.9,9.3,9.1,9.1,9.3,9.5,9.3,9.3,
9.3,9.9,9.7,9.1,9.3,9.5,9.4,9.0,9.0,8.8,9.0,8.8,8.6,8.6,8.0,
8.0,8.0,8.0,8.6,8.0,8.0,8.0,7.6,8.6,9.6,9.6,10.0,9.4,9.3,9.2,
9.5,9.5,9.5,9.9,9.9,9.5,9.3,9.5,9.5,9.1,9.3,9.5,9.3,9.1,9.3,
9.1,9.5,9.4,9.5,9.6,10.2,9.8,9.6,9.6,9.4,9.4,9.4,9.4,9.6,9.6,
9.4,9.4,9.0,9.4,9.4,9.6,9.4,9.2,8.8,8.8,9.2,9.2,9.6,9.6,9.8,
9.8,10.0,10.0,9.4,9.8,8.8,8.8,8.8,8.8,9.6,9.6,9.6,9.2,9.2,9.0,
9.0,9.0,9.4,9.0,9.0,9.4,9.4,9.6,9.4,9.6,9.6,9.6,10.0,10.0,9.6,
9.2,9.2,9.2,9.0,9.0,9.6,9.8,10.2,10.0,10.0,10.0,9.4,9.2,9.6,9.7,
9.7,9.8,9.8,9.8,10.0,10.0,8.6,9.0,9.4,9.4,9.4,9.4,9.4,9.6,10.0,
10.0,9.8,9.8,9.7,9.6,9.4,9.2,9.0,9.4,9.6,9.6,9.6,9.6,9.6,9.6,
9.0,9.4,9.4,9.4,9.6,9.4,9.6,9.6,9.8,9.8,9.8,9.6,9.2,9.6,9.2,
9.2,9.6,9.6,9.6,9.6,9.6,9.6,10.0,10.0,10.4,10.4,9.8,9.0,9.6,9.8,
9.6,8.6,8.0,8.0,8.0,8.0,8.4,8.8,8.4,8.4,9.0,9.0,9.4,10.0,10.0,
10.0,10.2,10.0,10.0,9.6,9.0,9.0,8.6,9.0,9.6,9.6,9.0,9.0,8.9,8.8,
8.7,8.6,8.3,7.9};
/* Actual values of series D at time points t=305,...,t=310 */
float actual[6] = {8.5,8.7,8.9,9.1,9.1,9.1};
char *col_labels[] = {
"Lead Time",
"Orig. Series",
"Forecast",
"Dev. for Prob. Limits",
"Psi"};
n_predict = 6;
n_obs = 304;
/* Define times from t=1 to t=304 */
for (i=0;i<n_obs;i++) times[i] = i+1;
imsls_f_auto_arima(n_obs, times, x,
IMSLS_MODEL, model,
IMSLS_AIC, &aic,
IMSLS_CRITICAL, 3.8,
IMSLS_MAX_LAG, 5,
IMSLS_METHOD, 2,
IMSLS_P_INITIAL, n_p_initial, p_initial,
IMSLS_Q_INITIAL, n_q_initial, q_initial,
IMSLS_S_INITIAL, n_s_initial, s_initial,
IMSLS_D_INITIAL, n_d_initial, d_initial,
IMSLS_NUM_OUTLIERS, &num_outliers,
IMSLS_OUTLIER_STATISTICS_USER, outlier_stat,
IMSLS_RESIDUAL_SIGMA, &res_sigma,
IMSLS_NUM_PREDICT, n_predict,
IMSLS_OUTLIER_FORECAST_USER, outlier_forecast,
IMSLS_RETURN_USER, parameters,
0);
printf("\nMethod 2: Grid search, differencing allowed\n");
printf("\nModel chosen: p=%d, q=%d, s=%d, d=%d\n", model[0],
model[1], model[2], model[3]);
printf("\nNumber of outliers: %d\n\n", num_outliers);
printf("Outlier statistics:\n\n");
printf("Time point Outlier type\n");
for (i=0; i<num_outliers; i++)
printf("%d%11d\n", outlier_stat[2*i], outlier_stat[2*i+1]);
printf("\nAIC = %lf\n", aic);
printf("RSE = %lf\n\n", res_sigma);
printf("Parameters:\n");
for (i=0; i<=model[0]+model[1]; i++)
printf("parameters[%d] = %lf\n", i, parameters[i]);
for (i=0; i<n_predict; i++)
{
forecast_table[4*i] = actual[i];
forecast_table[4*i+1] = outlier_forecast[3*i];
forecast_table[4*i+2] = outlier_forecast[3*i+1];
forecast_table[4*i+3] = outlier_forecast[3*i+2];
}
imsls_f_write_matrix("* * * Forecast Table * * *",
n_predict, 4, forecast_table,
IMSLS_COL_LABELS, col_labels,
IMSLS_WRITE_FORMAT, "%11.4f", 0);
}
Output
Method 2: Grid search, differencing allowed
Model chosen: p=3, q=1, s=1, d=0
Number of outliers: 1
Outlier statistics:
Time point Outlier type
217 3
AIC = 675.885986
RSE = 0.286720
Parameters:
parameters[0] = 1.892720
parameters[1] = 0.184380
parameters[2] = 0.641278
parameters[3] = -0.029176
parameters[4] = -0.743030
* * * Forecast Table * * *
Lead Time Orig. Series Forecast Dev. for Prob. Psi
Limits
1 8.5000 8.0471 0.5620 0.9274
2 8.7000 8.2004 0.7664 0.8123
3 8.9000 8.3347 0.8921 0.7153
4 9.1000 8.4534 0.9785 0.6257
5 9.1000 8.5569 1.0397 0.5504
6 9.1000 8.6483 1.0847 0.4819
Example 3
This example is the same as Example 2 but now Method 3 with the optimum model parameters
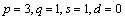 from Example 2 are chosen for
outlier detection and forecasting.
from Example 2 are chosen for
outlier detection and forecasting.
#include <imsls.h>
#include <stdio.h>
int main()
{
int n_obs, n_predict, i, num_outliers;
int *outlier_stat = NULL;
int model[4] = {3,1,1,0}, times[304];
float aic, res_sigma, *parameters = NULL;
float outlier_forecast[18], forecast_table[24];
/* Values of series D at time points t=1,...,t=304 */
float x[304] = {
8.0,8.0,7.4,8.0,8.0,8.0,8.0,8.8,8.4,8.4,8.0,8.2,8.2,8.2,8.4,
8.4,8.4,8.6,8.8,8.6,8.6,8.6,8.6,8.6,8.8,8.9,9.1,9.5,8.5,8.4,
8.3,8.2,8.1,8.3,8.4,8.7,8.8,8.8,9.2,9.6,9.0,8.8,8.6,8.6,8.8,
8.8,8.6,8.6,8.4,8.3,8.4,8.3,8.3,8.1,8.2,8.3,8.5,8.1,8.1,7.9,
8.3,8.1,8.1,8.1,8.4,8.7,9.0,9.3,9.3,9.5,9.3,9.5,9.5,9.5,9.5,
9.5,9.5,9.9,9.5,9.7,9.1,9.1,8.9,9.3,9.1,9.1,9.3,9.5,9.3,9.3,
9.3,9.9,9.7,9.1,9.3,9.5,9.4,9.0,9.0,8.8,9.0,8.8,8.6,8.6,8.0,
8.0,8.0,8.0,8.6,8.0,8.0,8.0,7.6,8.6,9.6,9.6,10.0,9.4,9.3,9.2,
9.5,9.5,9.5,9.9,9.9,9.5,9.3,9.5,9.5,9.1,9.3,9.5,9.3,9.1,9.3,
9.1,9.5,9.4,9.5,9.6,10.2,9.8,9.6,9.6,9.4,9.4,9.4,9.4,9.6,9.6,
9.4,9.4,9.0,9.4,9.4,9.6,9.4,9.2,8.8,8.8,9.2,9.2,9.6,9.6,9.8,
9.8,10.0,10.0,9.4,9.8,8.8,8.8,8.8,8.8,9.6,9.6,9.6,9.2,9.2,9.0,
9.0,9.0,9.4,9.0,9.0,9.4,9.4,9.6,9.4,9.6,9.6,9.6,10.0,10.0,9.6,
9.2,9.2,9.2,9.0,9.0,9.6,9.8,10.2,10.0,10.0,10.0,9.4,9.2,9.6,9.7,
9.7,9.8,9.8,9.8,10.0,10.0,8.6,9.0,9.4,9.4,9.4,9.4,9.4,9.6,10.0,
10.0,9.8,9.8,9.7,9.6,9.4,9.2,9.0,9.4,9.6,9.6,9.6,9.6,9.6,9.6,
9.0,9.4,9.4,9.4,9.6,9.4,9.6,9.6,9.8,9.8,9.8,9.6,9.2,9.6,9.2,
9.2,9.6,9.6,9.6,9.6,9.6,9.6,10.0,10.0,10.4,10.4,9.8,9.0,9.6,9.8,
9.6,8.6,8.0,8.0,8.0,8.0,8.4,8.8,8.4,8.4,9.0,9.0,9.4,10.0,10.0,
10.0,10.2,10.0,10.0,9.6,9.0,9.0,8.6,9.0,9.6,9.6,9.0,9.0,8.9,8.8,
8.7,8.6,8.3,7.9};
/* Actual values of series D at time points t=305,...,t=310 */
float actual[6] = {8.5,8.7,8.9,9.1,9.1,9.1};
char *col_labels[] = {
"Lead Time",
"Orig. Series",
"Forecast",
"Dev. for Prob. Limits",
"Psi"};
n_predict = 6;
n_obs = 304;
/* Define times from t=1 to t=304 */
for (i=0;i<n_obs;i++) times[i] = i+1;
parameters = imsls_f_auto_arima(n_obs, times, x,
IMSLS_MODEL, model,
IMSLS_AIC, &aic,
IMSLS_CRITICAL, 3.8,
IMSLS_METHOD, 3,
IMSLS_NUM_OUTLIERS, &num_outliers,
IMSLS_OUTLIER_STATISTICS, &outlier_stat,
IMSLS_RESIDUAL_SIGMA, &res_sigma,
IMSLS_NUM_PREDICT, n_predict,
IMSLS_OUTLIER_FORECAST_USER, outlier_forecast,
0);
printf("\nMethod 3: Specified ARIMA model\n");
printf("\nModel: p=%d, q=%d, s=%d, d=%d\n", model[0], model[1],
model[2], model[3]);
printf("\nNumber of outliers: %d\n\n", num_outliers);
printf("Outlier statistics:\n\n");
printf("Time point Outlier type\n");
for (i=0; i<num_outliers; i++)
printf("%d%11d\n", outlier_stat[2*i], outlier_stat[2*i+1]);
printf("\nAIC = %lf\n", aic);
printf("RSE = %lf\n", res_sigma);
printf("\nParameters:\n");
for (i=0; i<=model[0]+model[1]; i++)
printf("parameters[%d] = %lf\n", i, parameters[i]);
for (i=0; i<n_predict; i++)
{
forecast_table[4*i] = actual[i];
forecast_table[4*i+1] = outlier_forecast[3*i];
forecast_table[4*i+2] = outlier_forecast[3*i+1];
forecast_table[4*i+3] = outlier_forecast[3*i+2];
}
imsls_f_write_matrix("* * * Forecast Table * * *",
n_predict, 4, forecast_table,
IMSLS_COL_LABELS, col_labels,
IMSLS_WRITE_FORMAT, "%11.4f", 0);
}
Output
Method 3: Specified ARIMA model
Model: p=3, q=1, s=1, d=0
Number of outliers: 1
Outlier statistics:
Time point Outlier type
217 3
AIC = 675.885925
RSE = 0.286720
Parameters:
parameters[0] = 1.892720
parameters[1] = 0.184380
parameters[2] = 0.641278
parameters[3] = -0.029176
parameters[4] = -0.743030
* * * Forecast Table * * *
Lead Time Orig. Series Forecast Dev. for Prob. Psi
Limits
1 8.5000 8.0471 0.5620 0.9274
2 8.7000 8.2004 0.7664 0.8123
3 8.9000 8.3347 0.8921 0.7153
4 9.1000 8.4534 0.9785 0.6257
5 9.1000 8.5569 1.0397 0.5504
6 9.1000 8.6483 1.0847 0.4819

