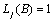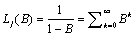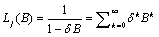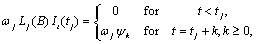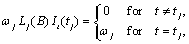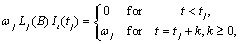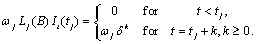Computes forecasts, their associated probability
limits and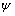 
weights for an outlier contaminated
time series whose underlying outlier free series follows a general seasonal
or nonseasonal ARMA model.
Synopsis
#include <imsls.h>
float
*imsls_f_ts_outlier_forecast (int
n_obs, float
series[],
int
num_outliers, int
outlier_statistics[], float
omega[],
float
delta, int
model[], float
parameters[],
int n_predict,…,0)
The type double function is imsls_d_ts_outlier_forecast.
Required Arguments
int n_obs
(Input)
Number of observations in the time series.
float series[]
(Input)
An array of length n_obs by 2 containing
the outlier free time series in its first column and the residuals of the series
in the second column.
int num_outliers
(Input)
Number of detected outliers in the original outlier
contaminated series as computed in imsls_f_ts_outlier_identification.
int outlier_statistics[] (Input)
An array of length num_outliers
by 2 containing the outlier statistics from imsls_f_ts_outlier_identification.
If num_outliers=0, this array is ignored.
float omega[]
(Input)
Array of length num_outliers
containing the 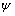weights for the outliers determined
in imsls_f_ts_outlier_identification.
Ignored, if num_outliers=0.
float delta
(Input)
The dynamic dampening effect parameter used in the outlier
detection.
int model[] (Input)
Vector of length 4 containing the numbers p, q, s, d of the
ARIMA
model the outlier free series
is following.
float parameters[]
(Input)
Vector of length 1+p+q containing
the estimated constant, AR and MA parameters as output from imsls_f_ts_outlier_identification.
int n_predict
(Input)
Maximum lead time for forecasts. The forecasts are
taken at origin t=n_obs, the time point
of the last observed value, for lead times 1,2,...,n_predict.
Return Value
Pointer to an array of length n_predict
by 3. The first column contains the forecasted values for the original
outlier contaminated series. The second column contains the
deviations from each forecast for computing confidence probability limits, and the third
column contains the 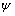weights of the infinite moving
average form of the model.
If an error occurred, NULL is returned.
Synopsis with Optional Arguments
#include <imsls.h>
float
*imsls_f_ts_outlier_forecast(int
n_obs,
float series[],
int
num_outliers, int
outlier_statistics[],
float
omega[], float
delta, int
model[],
float
parameters[], int
n_predict,
IMSLS_RETURN_USER, float
forecast[],
IMSLS_CONFIDENCE, float
confidence,
IMSLS_OUT_FREE_FORECAST, float
**outfree_forecast,
IMSLS_OUT_FREE_FORECAST_USER, float
outfree_forecast[],
0)
Optional Arguments
IMSLS_RETURN_USER, float forecast[] (Output)
An array
of length n_predict by 3
supplied by the user containing the forecasts for the original outlier
contaminated series in column 1, deviations from each forecast in column 2 and
the 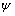weights of the infinite moving
average form of the model in column 3.
IMSLS_CONFIDENCE,
float
confidence (Input)
Value in the
exclusive interval (0,100) used to specify the confidence percent
probability limits of the forecast.Typical choices for confidence are
90.0, 95.0 and 99.0.
Default: confidence = 95.0
IMSLS_OUT_FREE_FORECAST,
float
**outfree_forecast (Output)
Address of a
pointer to an array of length n_predict by 3 containing the forecasts for the
original outlier free series in column 1, deviations from each forecast in
column 2 and the 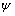weights of the infinite moving
average form of the model in column 3.
IMSLS_OUT_FREE_FORECAST_USER, float
outfree_forecast[]
Output)
Storage for array outfree_forecast is provided
by the user. For a description, see IMSLS_OUT_FREE_FORECAST.
Description
Consider the following model for a given
outlier contaminated univariate time series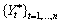 
:
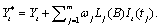
For an explanation of the notation, see the “Description”
section for imsls_f_ts_outlier_identification.
It follows from the formula above that
the Box-Jenkins forecast at origin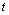 
for lead time 
, 
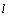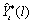, can be computed as:
Therefore, computation of the forecasts for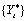 
is done in two steps:
1. Computation of the forecasts for the outlier free series 
.
2. Computation of the forecasts for
the original series 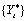by adding the multiple outlier
effects to the forecasts for .
Step 1 above:
Since
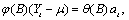
where
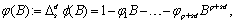
the Box-Jenkins forecast at origin 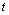for lead time , 
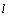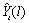, can be computed recursively as:
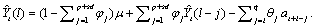
Here,
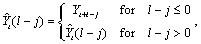
and
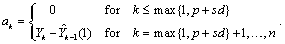
Step 2 above:
The formulas for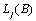 
for the different types of
outliers are as follows:
|
Innovational outliers (IO) |
|
|
Additive outliers (AO) |
|
|
Level shifts (LS) |
|
|
Temporary changes (TC) |
|
Assuming the outlier occurs at time point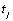 
, the outlier impact is
therefore:
|
Innovational outliers (IO) |
|
|
Additive outliers (AO) |
|
|
Level shifts (LS) |
|
|
Temporary changes (TC) |
|
From these formulas, the forecasts 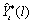can be computed easily.
The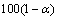 
percent probability
limits for 
and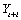 
are given by
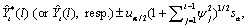
where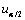 
is the 
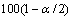percentile of the standard
normal distribution,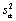 
is an estimate of the variance
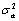of the random shocks (returned
from imsls_f_ts_outlier_identification),
and the 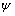weights 
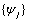are the coefficients in
Example
This example is a realization of an ARMA(2,1) process
described by the model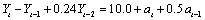 
,
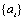a Gaussian white
noise process.
Outliers were artificially added to the outlier free series
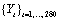at time points 
(level shift,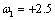 
) and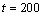 
(additive outlier, 
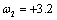), resulting in the outlier
contaminated series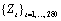 
. For both series, forecasts
were determined for time points 
and compared with the
actual values of the series.
#include <imsls.h>
#include <stdlib.h>
#include <stdio.h>
int main()
{
float time_series[290] ={
41.6699982,41.6699982,42.0752144,42.6123962,43.6161919,42.1932831,
43.1055450,44.3518715,45.3961258,45.0790215,41.8874397,40.2159805,
40.2447319,39.6208458,38.6873589,37.9272423,36.8718872,36.8310852,
37.4524879,37.3440933,37.9861374,40.3810501,41.3464622,42.6495285,
42.6096764,40.3134537,39.7971268,41.5401535,40.7160759,41.0363541,
41.8171883,42.4190292,43.0318832,43.9968109,44.0419617,44.3225212,
44.6082611,43.2199631,42.0419197,41.9679718,42.4926224,43.2091255,
43.2512283,41.2301674,40.1057358,40.4510574,41.5329170,41.5678177,
43.0090141,42.1592140,39.9234505,38.8394127,40.4319878,40.8679352,
41.4551926,41.9756317,43.9878922,46.5736389,45.5939293,42.4487762,
41.5325394,42.8830910,44.5771217,45.8541985,46.8249474,47.5686378,
46.6700745,45.4120026,43.2305107,42.7635345,43.7112923,42.0768661,
41.1835632,40.3352280,37.9761467,35.9550056,36.3212509,36.9925880,
37.2625008,37.0040665,38.5232544,39.4119797,41.8316803,43.7091446,
42.9381447,42.1066780,40.3771248,38.6518707,37.0550499,36.9447708,
38.1017685,39.4727097,39.8670387,39.3820763,38.2180786,37.7543488,
37.7265244,38.0290642,37.5531158,37.4685936,39.8233147,42.0480766,
42.4053535,43.0117416,44.1289330,45.0393829,45.1114540,45.0086479,
44.6560631,45.0278931,46.7830849,48.7649765,47.7991905,46.5339661,
43.3679199,41.6420822,41.2694893,41.5959740,43.5330009,43.3643608,
42.1471291,42.5552788,42.4521446,41.7629128,39.9476891,38.3217010,
40.5318718,42.8811569,44.4796944,44.6887932,43.1670265,41.2226143,
41.8330154,44.3721924,45.2697029,44.4174194,43.5068550,44.9793015,
45.0585403,43.2746620,40.3317070,40.3880501,40.2627106,39.6230278,
41.0305252,40.9262009,40.8326912,41.7084885,42.9038048,45.8650513,
46.5231590,47.9916115,47.8463135,46.5921936,45.8854408,45.9130440,
45.7450371,46.2964249,44.9394569,45.8141251,47.5284042,48.5527802,
48.3950577,47.8753052,45.8880005,45.7086983,44.6174774,43.5567932,
44.5891113,43.1778679,40.9405632,40.6206894,41.3330421,42.2759552,
42.4744949,43.0719833,44.2178459,43.8956337,44.1033440,45.6241455,
45.3724861,44.9167595,45.9180603,46.9077835,46.1666603,46.6013489,
46.6592331,46.7291603,47.1908340,45.9784355,45.1215782,45.6791115,
46.7379875,47.3036957,45.9968834,44.4669495,45.7734680,44.6315041,
42.9911766,46.3842583,43.7214432,43.5276833,41.3946495,39.7013168,
39.1033401,38.5292892,41.0096245,43.4535828,44.6525154,45.5725899,
46.2815285,45.2766647,45.3481712,45.5039482,45.6745682,44.0144806,
42.9305000,43.6785469,42.2500534,40.0007210,40.4477005,41.4432716,
42.0058670,42.9357758,45.6758842,46.8809929,46.8601494,47.0449791,
46.5420647,46.8939934,46.2963371,43.5479164,41.3864059,41.4046364,
42.3037987,43.6223717,45.8602371,47.3016396,46.8632469,45.4651413,
45.6275482,44.9968376,42.7558670,42.0218239,41.9883728,42.2571678,
44.3708687,45.7483635,44.8832512,44.7945862,44.8922577,44.7409401,
45.1726494,45.5686874,45.9946709,47.3151054,48.0654068,46.4817467,
42.8618279,42.4550323,42.5791168,43.4230957,44.7787971,43.8317108,
43.6481781,42.4183960,41.8426285,43.3475227,44.4749908,46.3498306,
47.8599319,46.2449913,43.6044006,42.4563484,41.2715340,39.8492508,
39.9997292,41.4410820,42.9388237,42.5687332,42.6384087,41.7088661,
43.9399033,45.4284401,44.4558411,45.1761856,45.3489113,45.1892662,
46.3754730,45.6082802 };
int n_obs = 280, i;
float *parameters = NULL, *result = NULL, *forecast = NULL;
float *outfree_forecast = NULL, *omega = NULL, *residual = NULL;
float res_sigma, aic;
float delta = 0.7;
float series[560];
int *outlier_stat = NULL;
int num_outliers;
int n_predict = 10;
int model[4];
float forecast_table[40];
model[0] = 2;
model[1] = 1;
model[2] = 1;
model[3] = 0;
result = imsls_f_ts_outlier_identification(n_obs, model,
time_series,
IMSLS_RELATIVE_ERROR, 1.0e-5,
IMSLS_NUM_OUTLIERS, &num_outliers,
IMSLS_RESIDUAL, &residual,
IMSLS_OUTLIER_STATISTICS, &outlier_stat,
IMSLS_OMEGA_WEIGHTS, &omega,
IMSLS_ARMA_PARAM, ¶meters,
IMSLS_RESIDUAL_SIGMA, &res_sigma,
IMSLS_AIC, &aic,
0);
printf("\nARMA parameters:\n");
for (i=0; i<=model[0]+model[1]; i++)
printf("%d\t\t%lf\n", i, parameters[i]);
printf("\nNumber of outliers: %d\n\n", num_outliers);
printf("Outlier statistics:\n");
printf("Time point\t\tOutlier type\n");
for (i=0; i<num_outliers; i++)
printf("%d\t\t%d\n", outlier_stat[2*i], outlier_stat[2*i+1]);
printf("\n");
printf("RSE:%lf\n", res_sigma);
printf("AIC:%lf\n", aic);
for (i=0; i<n_obs; i++)
{
series[2*i] = result[i];
series[2*i+1] = residual[i];
}
forecast = imsls_f_ts_outlier_forecast(n_obs, series,
num_outliers, outlier_stat, omega, delta,
model, parameters, n_predict,
IMSLS_OUT_FREE_FORECAST,&outfree_forecast, 0);
for (i=0; i<n_predict; i++)
{
forecast_table[4*i] = time_series[n_obs+i];
forecast_table[4*i+1] = forecast[3*i];
forecast_table[4*i+2] = forecast[3*i+1];
forecast_table[4*i+3] = forecast[3*i+2];
}
imsls_f_write_matrix("\t* * * Forecast Table for outlier"
"contaminated series * * *\nOrig. Series"
"\tforecast\tprob. limits\tpsi weights\n",
n_predict, 4, forecast_table,
IMSLS_WRITE_FORMAT, "%11.4f", 0);
for (i=0; i<n_predict; i++)
{
forecast_table[4*i] = time_series[n_obs+i] - 2.5;
forecast_table[4*i+1] = outfree_forecast[3*i];
forecast_table[4*i+2] = outfree_forecast[3*i+1];
forecast_table[4*i+3] = outfree_forecast[3*i+2];
}
printf("\n");
imsls_f_write_matrix("\t* * * Forecast Table for outlier free"
"series * * *\n\nOutlier free series\tforecast"
"\tprob. limits\tpsi weights\n",
n_predict, 4, forecast_table,
IMSLS_WRITE_FORMAT, "%11.4f", 0);
}
Output
ARMA parameters:
0 8.839014
1 0.948735
2 -0.153870
3 -0.553387
Number of outliers: 2
Outlier statistics:
Time point Outlier type
150 2
200 1
RSE:1.004321
AIC:1323.625977
* * * Forecast Table for outlier contaminated series * * *
Orig. series forecast prob. limits psi weights
1 2 3 4
1 42.6384 42.3178 1.9684 1.5021
2 41.7089 42.7910 3.5521 1.2712
3 43.9399 43.2786 4.3450 0.9749
4 45.4284 43.6684 4.7500 0.7294
5 44.4558 43.9632 4.9622 0.5420
6 45.1762 44.1828 5.0756 0.4019
7 45.3489 44.3459 5.1369 0.2979
8 45.1893 44.4668 5.1703 0.2208
9 46.3755 44.5564 5.1885 0.1637
10 45.6083 44.6228 5.1985 0.1213
* * * Forecast Table for outlier free series * * *
Outlier free series forecast prob. limits psi weights
1 2 3 4
1 40.1384 40.5936 1.9684 1.5021
2 39.2089 41.0668 3.5521 1.2712
3 41.4399 41.5544 4.3450 0.9749
4 42.9284 41.9442 4.7500 0.7294
5 41.9558 42.2389 4.9622 0.5420
6 42.6762 42.4586 5.0756 0.4019
7 42.8489 42.6217 5.1369 0.2979
8 42.6893 42.7426 5.1703 0.2208
9 43.8755 42.8322 5.1885 0.1637
10 43.1083 42.8986 5.1985 0.1213
