Constructs an equivalent completely testable multivariate general linear hypothesis HβU = G  from a partially testable hypothesis H_pβU = G_p.

Synopsis

#include <imsls.h>

int imsls_f_hypothesis_partial (Imsls_f_regression *regression_info, int nhp, float hp[], ..., 0)

The type double function is imsls_d_hypothesis_partial.

Required Argument

Imsls_f_regression *regression_info   (Input)
Pointer to a structure of type Imsls_f_regression containing information about the regression fit. See function imsls_f_regression.

int nhp   (Input)
Number of rows in the hypothesis matrix, hp.

float hp[]   (Input)
The H_p array of size nhp by n_coefficients with each row corresponding to a row in the hypothesis and containing the constants that specify a linear combination of the regression coefficients. Here, n_coefficients is the number of coefficients in the fitted regression model.

Return Value

Number of rows in the completely testable hypothesis, nh. This value is also the degrees of freedom for the hypothesis. The value nh classifies the hypothesis H_pβU = G_p as nontestable (nh = 0), partially testable (0 < nh < rank_hp) or completely testable (0 < nh = rank_hp), where rank_hp is the rank of H_p (see keyword IMSLS_RANK_HP).

Synopsis with Optional Arguments

#include <imsls.h>

int imsls_f_hypothesis_partial (Imsls_f_regression *regression_info, int nhp, float hp[],
IMSLS_GP, float gp[],
IMSLS_U, int nu, float u[],
IMSLS_RANK_HP, int rank_hp
IMSLS_H_MATRIX, float **h,
IMSLS_H_MATRIX_USER, float h[],
IMSLS_G, float **g,
IMSLS_G_USER, float g[],
0)

Optional Arguments

IMSLS_GP, float gp[]   (Input)
Array of size nhp by nu containing the G_p matrix, the null hypothesis values. By default, each value of G_p is equal to 0.

IMSLS_U, int nu, float u[]   (Input)
Argument nu is the number of linear combinations of the dependent variables to be considered. The value nu must be greater than 0 and less than or equal to n_dependent.

            Argument u contains the n_dependent by nu U matrix for the test H_pBU = G_p. This argument is not referenced by imsls_f_hypothesis_partial and is included only for consistency with functions imsls_f_hypothesis_scph and imsls_f_hypothesis_test. A dummy array of length 1 may be substituted for this argument.

            Default: nu = n_dependent and u is the identity matrix.

IMSLS_RANK_HP, int*rank_hp   (Output)
Rank of H_p.

IMSLS_H_MATRIX, float **h   (Output)
Address of a pointer to the internally allocated array of size nhp by n_parameters containing the H matrix. Each row of h corresponds to a row in the completely testable hypothesis and contains the constants that specify an estimable linear combination of the regression coefficients.  The actual size of H is nh by n_paramters, where nh is the number of rows in the completely testable hypothesis returned by imsls_f_hypothesis_partial. Note that nh may be less than or equal to nhp.

IMSLS_H_MATRIX_USER, float h[]   (Output)
Storage for array h is provided by the user. See IMSLS_H.

IMSLS_G, float **g   (Output)
Address of a pointer to the internally allocated array of size nph ny n_dependent containing the G matrix. The elements of g contain the null hypothesis values for the completely testable hypothesis.  The actual size of G is nh by n_dependent, where nh is the number of rows in the completely testable hypothesis returned by imsls_f_hypothesis_partial. Note that nh may be less than or equal to nhp.

IMSLS_G_USER, float g[]   (Output)
Storage for array g is provided by the user. See IMSLS_G.

Description

Once a general linear model y = Xβ + ɛ is fitted, particular hypothesis tests are frequently of interest. If the matrix of regressors X is not full rank (as evidenced by the fact that some diagonal elements of the R matrix output from the fit are equal to zero), methods that use the results of the fitted model to compute the hypothesis sum of squares (see function imsls_f_hypothesis_scph) require specification in the hypothesis of only linear combinations of the regression parameters that are estimable. A linear combination of regression parameters c^Tβ is estimable if there exists some vector a such that c^T = a^TX, i.e., c^T is in the space spanned by the rows of X. For a further discussion of estimable functions, see Maindonald (1984, pp. 166−168) and Searle (1971, pp. 180−188). Function imsls_f_hypothesis_partial is only useful in the case of non-full rank regression models, i.e., when the problem of estimability arises.

Peixoto (1986) noted that the customary definition of testable hypothesis in the context of a general linear hypothesis test Hβ = g is overly restrictive. He extended the notion of a testable hypothesis (a hypothesis composed of estimable functions of the regression parameters) to include partially testable and completely testable hypothesis. A hypothesis Hβ = g is partially testable if the intersection of the row space H (denoted by ℜ(H)) and the row space of X (ℜ(X)) is not essentially empty and is a proper subset of ℜ(H), i.e., {0} ⊂ ℜ(H) ∩ ℜ(X) ⊂ ℜ(H). A hypothesis Hβ = g is completely testable if {0} ⊂ ℜ(H) ∩ ℜ(H) ⊂ ℜ(X). Peixoto also demonstrated a method for converting a partially testable hypothesis to one that is completely testable so that the usual method for obtaining sums of squares for the hypothesis from the results of the fitted model can be used. The method replaces H_p in the partially testable hypothesis H_pβ = g_p by a matrix H whose rows are a basis for the intersection of the row space of H_p and the row space of X. A corresponding conversion of the null hypothesis values from g_p to g is also made. A sum of squares for the completely testable hypothesis can then be computed (see function imsls_f_hypothesis_scph). The sum of squares that is computed for the hypothesis Hβ = g equals the difference in the error sums of squares from two fitted models—the restricted model with the partially testable hypothesis H_pβ = g_p and the unrestricted model.

For the general case of the multivariate model Y = Xβ + ɛ with possible linear equality restrictions on the regression parameters, imsls_f_hypothesis_partial converts the partially testable hypothesis H_pβ = g_p to a completely testable hypothesis HβU = G. For the case of the linear model with linear equality restrictions, the definitions of the estimable functions, nontestable hypothesis, partially testable hypothesis, and completely testable hypothesis are similar to those previously given for the unrestricted model with the exception that ℜ(X) is replaced by ℜ(R) where R is the upper triangular matrix based on the linear equality restrictions. The nonzero rows of R form a basis for the rowspace of the matrix (X^T, A^T)^T. The rows of H form an orthonormal basis for the intersection of two subspaces—the subspace spanned by the rows of H_p and the subspace spanned by the rows of R. The algorithm used for computing the intersection of these two subspaces is based on an algorithm for computing angles between linear subspaces due to Björk and Golub (1973). (See also Golub and Van Loan 1983, pp. 429−430). The method is closely related to a canonical correlation analysis dis­cussed by Kennedy and Gentle (1980, pp. 561−565). The algorithm is as follows:

1.     Compute a QR factorization of

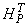
with column permutations so that

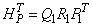
Here, P₁ is the associated permutation matrix that is also an orthogonal matrix. Determine the rank of H_p as the number of nonzero diagonal elements of R₁, for example n₁. Partition Q₁ = (Q₁₁, Q₁₂) so that Q₁₁ is the first n₁ column of Q₁. Set rank_hp = n.

2.     Compute a QR factorization of the transpose of the R matrix (input through regression_info) with column permuations so that

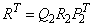
Determine the rank of R from the number of nonzero diagonal elements of R, for example n₂. Partition Q₂ = (Q₂₁, Q₂₂) so that Q₂₁ is the first n₂ columns of Q₂.

3.     Form

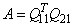
4.     Compute the singular values of A

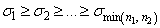
and the left singular vectors W of the singular value decomposition of A so that

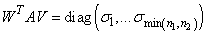
If σ₁ < 1, then the dimension of the intersection of the two subspaces is s = 0. Otherwise, assume the dimension of the intersection to be s if σ_s = 1 > σ_s+1. Set nh = s.

5.     Let W₁ be the first s columns of W. Set H = (Q₁W₁)^T.

6.     Assume R₁₁ to be a nhp by nhp matrix related to R₁ as follows: If nhp < n_parameters, R₁₁ equals the first nhp rows of R₁. Otherwise, R₁₁ contains R₁ in its first n_parameters rows and zeros in the remaining rows. Compute a solution Z to the linear system

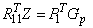
If this linear system is delcared inconsistent, an error message with error code equal to 2 is issued.

7.     Partition

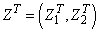
so that Z₁ is the first n₁ rows of Z. Set

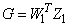
The degrees of freedom (nh) classify the hypothesis H_pβU =G_p as nontestable (nh = 0), partially testable (0 < nh < rank_hp), or completely testable (0 < nh = rank_hp).

For further details concerning the algorithm, see Sallas and Lionti (1988).

Example

A one-way analysis-of-variance model discussed by Peixoto (1986) is fitted to data. The model is

y_ii = μ + α_i + ɛ_ii                      (i, j) = (1, 1) (2, 1) (2, 2)

The model is fitted using function imsls_f_regression. The partially testable hypothesis

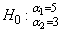
is converted to a completely testable hypothesis.

 

#include <imsls.h>

#define N_ROWS 3

#define N_INDEPENDENT 1

#define N_DEPENDENT 1

#define N_PARAMETERS 3

#define NHP 2

 

int main() {

    Imsls_f_regression *info;

    int    n_class = 1;

    int    n_continuous = 0;

    int    nh, nreg, rank_hp;

    float  *coefficients, *x, *g, *h;

    static float   z[N_ROWS*N_INDEPENDENT] = { 1, 2, 2 };

    static float   y[] = {17.3, 24.1, 26.3};

    static float   gp[] = {5, 3};

    static float   hp[NHP*N_PARAMETERS] = {0, 1, 0,

                                           0, 0, 1};

 

    nreg = imsls_f_regressors_for_glm(N_ROWS, z,

        n_class, n_continuous,

        IMSLS_REGRESSORS, &x, 0);   

 

    coefficients = imsls_f_regression(N_ROWS, nreg, x, y,

        IMSLS_N_DEPENDENT, N_DEPENDENT,

        IMSLS_REGRESSION_INFO, &info,

        0);

 

    nh = imsls_f_hypothesis_partial(info, NHP, hp,

        IMSLS_GP, gp,

        IMSLS_H_MATRIX, &h,

        IMSLS_G, &g,

        IMSLS_RANK_HP, &rank_hp, 0);

 

    if (nh == 0) {

        printf("Nontestable Hypothesis\n");

    } else if (nh < rank_hp) {

        printf("Partially Testable Hypothesis\n");

    } else {

        printf("Completely Testable Hypothesis\n");

    }

 

    imsls_f_write_matrix("H Matrix", nh, N_PARAMETERS, h, 0);

 

    imsls_f_write_matrix("G", nh, N_DEPENDENT, g, 0);

 

    imsls_free(coefficients);

    imsls_free(info);

    imsls_free(x);

    imsls_free(h);

    imsls_free(g);   

}

Output

Partially Testable Hypothesis

 

             H Matrix

         1           2           3

    0.0000      0.7071     -0.7071

 

     G

     1.414

Warning Errors

IMSLS_HYP_NOT_CONSISTENT            The hypothesis is inconsistent within the computed tolerance.

---

Contact Support