regression

Chapter 2: Regression > regression

regression

Fits a multivariate linear regression model using least squares.

Synopsis

#include <imsls.h>

float *imsls_f_regression (int n_rows, int n_independent, float x[], float y[], ..., 0)

The type double function is imsls_d_regression.

Required Arguments

int n_rows (Input)
Number of rows in x.

int n_independent (Input)
Number of independent (explanatory) variables.

float x[] (Input)
Array of size n_rows × n_independent containing the independent (explanatory) variables(s). The i-th column of x contains the i-th independent variable.

float y[] (Input)
Array of size n_rows × n_dependent containing the dependent (response) variables(s). The i-th column of y contains the i-th dependent variable. See optional argument IMSLS_N_DEPENDENT to set the value of n_dependent.

Return Value

If the optional argument IMSLS_NO_INTERCEPT is not used, regression returns a pointer to an array of length n_dependent × (n_independent + 1) containing a least-squares solution for the regression coefficients. The estimated intercept is the initial component of each row, where the i-th row contains the regression coefficients for the i-th dependent variable.

Synopsis with Optional Arguments

#include <imsls.h>

float *imsls_f_regresssion (int n_rows, int n_independent,

IMSLS_X_COL_DIM, int x_col_dim,

IMSLS_Y_COL_DIM, int y_col_dim,IMSLS_N_DEPENDENT, int n_dependent,

IMSLS_X_INDICES, int indind[], int inddep[], int ifrq, int iwt,

IMSLS_IDO, int ido,

IMSLS_ROWS_ADD, or

IMSLS_ROWS_DELETE,

IMSLS_INTERCEPT, or

IMSLS_NO_INTERCEPT,

IMSLS_TOLERANCE, float tolerance,

IMSLS_RANK, int *rank,

IMSLS_COEF_COVARIANCES, float **coef_covariances,

IMSLS_COEF_COVARIANCES_USER, float coef_covariances[],

IMSLS_COV_COL_DIM, int cov_col_dim,

IMSLS_X_MEAN, float **x_mean,

IMSLS_X_MEAN_USER, float x_mean[],

IMSLS_RESIDUAL, float **residual,

IMSLS_RESIDUAL_USER, float residual[],

IMSLS_ANOVA_TABLE, float **anova_table,

IMSLS_ANOVA_TABLE_USER, float anova_table[],

IMSLS_FREQUENCIES, float frequencies[],

IMSLS_SCPE, float **scpe[],

IMSLS_SCPE_USER, float scpe_user[],

IMSLS_WEIGHTS, float weights[], \

IMSLS_REGRESSION_INFO, Imsls_f_regression **regression_info,

IMSLS_RETURN_USER, float coefficients[],

Optional Arguments

IMSLS_X_COL_DIM, int x_col_dim (Input)
Column dimension of x.
Default: x_col_dim = n_independent

IMSLS_Y_COL_DIM, int y_col_dim (Input)
Column dimension of y.
Default: y_col_dim = n_dependent

IMSLS_N_DEPENDENT, int n_dependent (Input)
Number of dependent variables. Input matrix y must be declared of size n_rows by n_dependent, where column i of y contains the i-th dependent variable.
Default: n_dependent = 1

IMSLS_X_INDICES, int indind[], int inddep, int ifrq, int iwt (Input)
This argument allows an alternative method for data specification. Data (independent, dependent, frequencies, and weights) is all stored in the data matrix x. Argument y, and keywords IMSLS_FREQUENCIES and IMSLS_WEIGHTS are ignored.

Each of the four arguments contains indices indicating column numbers of x in which particular types of data are stored. Columns are numbered 0 … x_col_dim − 1.

Parameter indind contains the indices of the independent variables.

Parameter inddep contains the indices of the dependent variables.

Parameters ifrq and iwt contain the column numbers of x in which the frequencies and weights, respectively, are stored. Set ifrq = −1 if there will be no column for frequencies. Set iwt = −1 if there will be no column for weights. Weights are rounded to the nearest integer. Negative weights are not allowed.

Note that required input argument y is not referenced, and can be declared a vector of length 1.

IMSLS_IDO, int ido (Input)
Processing option.
The argument ido must be one of 0, 1, 2, or 3. If ido = 0 (the default), all of the observations are input during one invocation. If ido = 1, 2, or 3, blocks of rows of the data can be processed squentially in separate invocations of imsls_f_regression; with this option, it is not a requirement that all observations be memory resident, thus enabling one to handle large data sets.

Ido	Action
0	This is the only invocation; all the data are input at once. (Default)
1	This is the first invocation with this data; additional calls will be made. Initialization and updating for the n_rows observations of x will be performed.
2	This is an intermediate invocation; updating for the n_rows observations of x will be performed.
3	This is the final invocation of this function. Updating for the data in x and wrap-up computations are performed. Workspace is released No further invocations of imsls_f_regression with ido greater than 1 should be made without first invoking imsls_f_regression with ido = 1.

Default: ido = 0

IMSLS_ROWS_ADD, or

IMSLS_ROWS_DELETE
By default (or if IMSLS_ROWS_ADD is specified), the observations in x are added to the discriminant statistics. If IMSLS_ROWS_DELETE is specified, then the observations are deleted.

If ido = 0, these optional arguments are ignored (data is always added if there is only one invocation).

IMSLS_INTERCEPT, or

IMSLS_NO_INTERCEPT
IMSLS_INTERCEPT is the default where the fitted value for observation i is

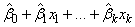
where k = n_independent. If IMSLS_NO_INTERCEPT is specified, the intercept term

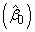
is omitted from the model and the return value from regression is a pointer to an array of length n_dependent × n_independent.

IMSLS_TOLERANCE, float tolerance (Input)
Tolerance used in determining linear dependence. For regression, tolerance = 100 × imsls_f_machine(4) is the default choice. For imsls_d_regression, tolerance = 100 × imsls_d_machine(4) is the default. (See imsls_f_machine Chapter 15 , “Ultilities”.)

IMSLS_RANK, int *rank (Output)
Rank of the fitted model is returned in *rank.

IMSLS_COEF_COVARIANCES, float **coef_covariances (Output)
Address of a pointer to the n_dependent × m × m internally allocated array containing the estimated variances and covariances of the estimated regression coefficients. Here, m is the number of regression coefficients in the model. If IMSLS_NO_INTERCEPT is specified, n = n_independent; otherwise, m = n_independent + 1.

The first m × m elements contain the matrix for the first dependent variable, the next m × m elements contain the matrix for the next dependent variable, ... and so on.

IMSLS_COEF_COVARIANCES_USER, float coef_covariances[] (Output)
Storage for arrays coef_covariances is provided by the user. See IMSLS_COEF_COVARIANCES.

IMSLS_COV_COL_DIM, int cov_col_dim (Input)
Column dimension of array coef_covariances.
Default: cov_col_dim = m, where m is the number of regression coefficients in the model

IMSLS_X_MEAN, float **x_mean (Output)
Address of a pointer to the internally allocated array containing the estimated means of the independent variables.

IMSLS_X_MEAN_USER, float x_mean[] (Output)
Storage for array x_mean is provided by the user.
See IMSLS_X_MEAN.

IMSLS_RESIDUAL, float **residual (Output)
Address of a pointer to the internally allocated array of size n_rows by n_dependent containing the residuals. Residuals may not be requested if ido > 0.

IMSLS_RESIDUAL_USER, float residual[] (Output)
Storage for array residual is provided by the user.
See IMSLS_RESIDUAL.

IMSLS_ANOVA_TABLE, float **anova_table (Output)
Address of a pointer to the internally allocated array of size
15 × n_dependent containing the analysis of variance table for each dependent variable. The i-th column corresponds to the analysis for the i-th dependent variable.

The analysis of variance statistics are given as follows:

Element	Analysis of Variance Statistics
0	degrees of freedom for the model
1	degrees of freedom for error
2	total (corrected) degrees of freedom
3	sum of squares for the model
4	sum of squares for error
5	total (corrected) sum of squares
6	model mean square
7	error mean square
8	overall F-statistic
9	p-value
10	R² (in percent)
11	adjusted R² (in percent)
12	estimate of the standard deviation
13	overall mean of y
14	coefficient of variation (in percent)

The anova statistics may not be requested if ido > 0. Note that the p-value is returned as 0.0 when the value is so small that all significant digits have been lost.

IMSLS_ANOVA_TABLE_USER, float anova_table[] (Output)
Storage for array anova_table is provided by the user. See IMSLS_ANOVA_TABLE.

IMSLS_SCPE, float **scpe (Output)
The address of a pointer to an internally allocated array of size n_dependent × n_dependent containing the error (residual) sums of squares and crossproducts. scpe [m][n] contains the sum of crossproducts for the m-th and n-th dependent variables.

IMSLS_SCPE_USER, float scpe[] (Output)
Storage for array scpe is provided by the user. See IMSLS_SCPE.

IMSLS_FREQUENCIES, float frequencies[] (Input)
Array of length n_rows containing the frequency for each observation.
Default: frequencies[] = 1

IMSLS_WEIGHTS, float weights[] (Input)
Array of length n_rows containing the weight for each observation.
Default: weights[] = 1

IMSLS_REGRESSION_INFO, Imsls_f_regression **regression_info (Output)
Address of the pointer to an internally allocated structure of type Imsls_f_regression containing information about the regression fit. This structure is required as input for functions imsls_f_regression_prediction and imsls_f_regression_summary.

IMSLS_RETURN_USER, float coefficients[] (Output)
If specified, the least-squares solution for the regression coefficients is stored in array coefficients provided by the user. If IMSLS_NO_INTERCEPT is specified, the array requires n_dependent × n units of memory, where n = n_independent; otherwise, n = n_independent + 1.

Description

Function imsls_f_regression fits a multivariate multiple linear regression model with or without an intercept. The multiple linear regression model is

y_i = β₀ + β₁x_i1 + β₂x_i2 + … + β_kx_ik + ɛ_i i = 1, 2, …, n

where the observed values of the y_i’s are the responses or values of the dependent variable; the x_i1’s, x_i2’s, …, x_ik’s are the settings of the k (input in n_independent) independent variables; β₀, β₁, …, β_k are the regression coefficients whose estimated values are to be output by imsls_f_regression; and the ɛ_i’s are independently distributed normal errors each with mean 0 and variance s². Here, n is the sum of the frequencies for all nonmissing observations, i.e.,

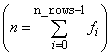
where f_i is equal to frequencies[i] if optional argument IMSLS_FREQUENCIES is specified and equal to 1.0 otherwise. Note that by default, β₀ is included in the model.

More generally, imsls_f_regression fits a multivariate regression model. See the chapter introduction for a description of the multivariate model.

Function imsls_f_regression computes estimates of the regression coefficients by minimizing the sum of squares of the deviations of the observed response y_i from the fitted response

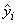
for the n observations. This minimum sum of squares (the error sum of squares) is output as one of the analysis of variance statistics if IMSLS_ANOVA_TABLE (or IMSLS_ANOVA_TABLE_USER) is specified and is computed as follows:

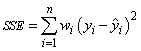
Another analysis of variance statistic is the total sum of squares. By default, the total sum of squares is the sum of squares of the deviations of y_i from its mean

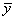
the so-called corrected total sum of squares. This statistic is computed as follows:

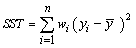
When IMSLS_NO_INTERCEPT is specified, the total sum of squares is the sum of squares of y_i, the so-called uncorrected total sum of squares. This is computed as follows:

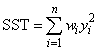
See Draper and Smith (1981) for a good general treatment of the multiple linear regression model, its analysis, and many examples.

In order to compute a least-squares solution, imsls_f_regression performs an orthogonal reduction of the matrix of regressors to upper-triangular form. The reduction is based on one pass through the rows of the augmented matrix (x, y) using fast Givens transformations. (See Golub and Van Loan 1983, pp. 156–162; Gentleman 1974.) This method has the advantage that the loss of accuracy resulting from forming the crossproduct matrix used in the normal equations is avoided.

By default, the current means of the dependent and independent variables are used to internally center the data for improved accuracy. Let x_i be a column vector containing the j-th row of data for the independent variables. Let x_i represent the mean vector for the independent variables given the data for rows 1, 2, …, i. The current mean vector is defined as follows:

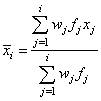
where the w_j’s and the f_j’s are the weights and frequencies. The i-th row of data has

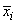
subtracted from it and is multiplied by

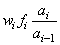
where

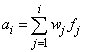
Although a crossproduct matrix is not computed, the validity of this centering operation can be seen from the following formula for the sum of squares and crossproducts matrix:

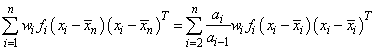
An orthogonal reduction on the centered matrix is computed. When the final computations are performed, the intercept estimate and the first row and column of the estimated covariance matrix of the estimated coefficients are updated (if IMSLS_COEF_COVARIANCES or IMSLS_COEF_COVARIANCES_USER is specified) to reflect the statistics for the original (uncentered) data. This means that the estimate of the intercept is for the uncentered data.

As part of the final computations, imsls_f_regression checks for linearly dependent regressors. In particular, linear dependence of the regressors is declared if any of the following three conditions are satisfied:

• A regressor equals 0.

• Two or more regressors are constant.

•

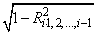
is less than or equal to tolerance. Here,

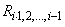
is the multiple correlation coefficient of the i-th independent variable with the first i – 1 independent variables. If no intercept is in the model, the multiple correlation coefficient is computed without adjusting for the mean.

On completion of the final computations, if the i-th regressor is declared to be linearly dependent upon the previous i − 1 regressors, the i-th coefficient estimate and all elements in the i-th row and i-th column of the estimated variance-covariance matrix of the estimated coefficients (if IMSLS_COEF_COVARIANCES or IMSLS_COEF_COVARIANCES_USER is specified) are set to 0. Finally, if a linear dependence is declared, an informational (error) message, code IMSLS_RANK_DEFICIENT, is issued indicating the model is not full rank.

Examples

Example 1

A regression model

y_i = β₀ + β₁x_i1 + β₂x_i2 + β₃x_i3 + ɛ_i i = 1, 2, …, 9

is fitted to data taken from Maindonald (1984, pp. 203–204).

#include <imsls.h>

#define INTERCEPT 1

#define N_INDEPENDENT 3

#define N_COEFFICIENTS (INTERCEPT + N_INDEPENDENT)

#define N_OBSERVATIONS 9

int main()

{

float *coefficients;

float x[][N_INDEPENDENT] = {7.0, 5.0, 6.0,

2.0,-1.0, 6.0,

7.0, 3.0, 5.0,

-3.0, 1.0, 4.0,

2.0,-1.0, 0.0,

2.0, 1.0, 7.0,

-3.0,-1.0, 3.0,

2.0, 1.0, 1.0,

2.0, 1.0, 4.0};

float y[] = {7.0,-5.0, 6.0, 5.0, 5.0, -2.0, 0.0, 8.0, 3.0};

coefficients = imsls_f_regression(N_OBSERVATIONS, N_INDEPENDENT,

(float *)x, y, 0);

imsls_f_write_matrix("Least-Squares Coefficients", 1, N_COEFFICIENTS,

coefficients,

IMSLS_COL_NUMBER_ZERO,

0);

}

Output

Least-Squares Coefficients

0 1 2 3

7.733 -0.200 2.333 -1.667

Example 2

A weighted least-squares fit is computed using the model

y_i = β₀ + β₁x_i1 + β₂x_i2 + ɛ_i i = 1, 2, …, 4

and weights 1∕i² discussed by Maindonald (1984, pp. 67−68).

In the example, IMSLS_WEIGHTS is specified. The minimum sum of squares for error in terms of the original untransformed regressors and responses for this weighted regression is

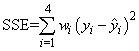
where w_i = 1/i², represented in the C code as array w.

#include <imsls.h>

#include <math.h>

#define N_INDEPENDENT 2

#define N_COEFFICIENTS N_INDEPENDENT + 1

#define N_OBSERVATIONS 4

int main()

{

int i;

float *coefficients, w[N_OBSERVATIONS], anova_table[15],

power;

float x[][N_INDEPENDENT] = {

-2.0, 0.0,

-1.0, 2.0,

2.0, 5.0,

7.0, 3.0};

float y[] = {-3.0, 1.0, 2.0, 6.0};

char *anova_row_labels[] = {

"degrees of freedom for regression",

"degrees of freedom for error",

"total (uncorrected) degrees of freedom",

"sum of squares for regression",

"sum of squares for error",

"total (uncorrected) sum of squares",

"regression mean square",

"error mean square", "F-statistic",

"p-value", "R-squared (in percent)",

"adjusted R-squared (in percent)",

"est. standard deviation of model error",

"overall mean of y",

"coefficient of variation (in percent)"};

/* Calculate weights */

power = 0.0;

for (i = 0; i < N_OBSERVATIONS; i++) {

power += 1.0;

w[i] = 1.0 / (power*power);

}

/*Perform analysis */

coefficients = imsls_f_regression(N_OBSERVATIONS, N_INDEPENDENT,

(float *) x, y,

IMSLS_WEIGHTS, w,

IMSLS_ANOVA_TABLE_USER, anova_table,

0);

/* Print results */

imsls_f_write_matrix("Least Squares Coefficients", 1,

N_COEFFICIENTS, coefficients, 0);

imsls_f_write_matrix("* * * Analysis of Variance * * *\n", 15, 1,

anova_table,

IMSLS_ROW_LABELS, anova_row_labels,

IMSLS_WRITE_FORMAT, "%10.2f",

0);

}

Output

Least Squares Coefficients

1 2 3

-1.431 0.658 0.748

* * * Analysis of Variance * * *

degrees of freedom for regression 2.00

degrees of freedom for error 1.00

total (uncorrected) degrees of freedom 3.00

sum of squares for regression 7.68

sum of squares for error 1.01

total (uncorrected) sum of squares 8.69

regression mean square 3.84

error mean square 1.01

F-statistic 3.79

p-value 0.34

R-squared (in percent) 88.34

adjusted R-squared (in percent) 65.03

est. standard deviation of model error 1.01

overall mean of y -1.51

coefficient of variation (in percent) -66.55

Example 3

A multivariate regression is performed for a data set with two dependent variables. Also, usage of the keyword IMSLS_X_INDICES is demonstrated. Note that the required input variable y is not referenced and is declared as a pointer to a float.

#include <imsls.h>

#define INTERCEPT 1

#define N_INDEPENDENT 3

#define N_DEPENDENT 2

#define N_COEFFICIENTS (INTERCEPT + N_INDEPENDENT)

#define N_OBSERVATIONS 9

int main()

{

float coefficients[N_DEPENDENT*N_COEFFICIENTS];

float *dummy;

float scpe[N_DEPENDENT*N_DEPENDENT];

float anova_table[15*N_DEPENDENT];

static float x[] = { 7.0, 5.0, 6.0, 7.0, 1.0,

2.0,-1.0, 6.0, -5.0, 4.0,

7.0, 3.0, 5.0, 6.0, 10.0,

-3.0, 1.0, 4.0, 5.0, 5.0,

2.0,-1.0, 0.0, 5.0, -2.0,

2.0, 1.0, 7.0, -2.0, 4.0,

-3.0,-1.0, 3.0, 0.0, -6.0,

2.0, 1.0, 1.0, 8.0, 2.0,

2.0, 1.0, 4.0, 3.0, 0.0};

int ifrq = -1, iwt=-1;

static int indind[N_INDEPENDENT] = {0, 1, 2};

static int inddep[N_DEPENDENT] = {3, 4};

char *fmt = "%10.4f";

char *anova_row_labels[] = {

"d.f. regression",

"d.f. error",

"d.f. total (uncorrected)",

"ssr",

"sse",

"sst (uncorrected)",

"msr",

"mse", "F-statistic",

"p-value", "R-squared (in percent)",

"adj. R-squared (in percent)",

"est. s.t.d. of model error",

"overall mean of y",

"coefficient of variation (in percent)"};

imsls_f_regression(N_OBSERVATIONS, N_INDEPENDENT,

(float *) x, dummy,

IMSLS_X_COL_DIM, N_INDEPENDENT+N_DEPENDENT,

IMSLS_N_DEPENDENT, N_DEPENDENT,

IMSLS_X_INDICES, indind, inddep, ifrq, iwt,

IMSLS_SCPE_USER, scpe,

IMSLS_ANOVA_TABLE_USER, anova_table,

IMSLS_RETURN_USER, coefficients,

0);

imsls_f_write_matrix("Least Squares Coefficients", N_DEPENDENT,

N_COEFFICIENTS, coefficients,

IMSLS_COL_NUMBER_ZERO, 0);

imsls_f_write_matrix("SCPE", N_DEPENDENT, N_DEPENDENT, scpe,

IMSLS_WRITE_FORMAT, "%10.4f", 0);

imsls_f_write_matrix("* * * Analysis of Variance * * *\n",

15, N_DEPENDENT,

anova_table,

IMSLS_ROW_LABELS, anova_row_labels,

IMSLS_WRITE_FORMAT, "%10.2f",

0);

}

Output

Least Squares Coefficients

0 1 2 3

1 7.733 -0.200 2.333 -1.667

2 -1.633 0.400 0.167 0.667

SCPE

1 2

1 4.0000 20.0000

2 20.0000 110.0000

* * * Analysis of Variance * * *

1 2

d.f. regression 3.00 3.00

d.f. error 5.00 5.00

d.f. total (uncorre 8.00 8.00

cted)

ssr 152.00 56.00

sse 4.00 110.00

sst (uncorrected) 156.00 166.00

msr 50.67 18.67

mse 0.80 22.00

F-statistic 63.33 0.85

p-value 0.00 0.52

R-squared (in 97.44 33.73

percent)

adj. R-squared 95.90 0.00

(in percent)

est. s.t.d. of 0.89 4.69

model error

overall mean of y 3.00 2.00

coefficient of 29.81 234.52

variation (in

percent)

Example 4

Continuing with Example 1 data, the example below invokes the regression function using values of IDO greater than 0. Also, usage of the keywords IMSLS_COEF_COVARIANCES and IMSLS_X_MEAN is demonstrated.

#include <imsls.h>

#define N_INDEPENDENT 3

#define N_OBSERVATIONS_BLOCK_1 3

#define N_OBSERVATIONS_BLOCK_2 3

#define N_OBSERVATIONS_BLOCK_3 3

#define N_COEFFICIENTS 4

int main()

{

float coefficients[N_COEFFICIENTS], *coef_covariance=NULL;

float *anova_table=NULL;

float *residual=NULL, *x_mean=NULL;

static float x1[][N_INDEPENDENT] = { 7.0, 5.0, 6.0,

2.0,-1.0, 6.0,

7.0, 3.0, 5.0};

static float x2[][N_INDEPENDENT] = {-3.0, 1.0, 4.0,

2.0,-1.0, 0.0,

2.0, 1.0, 7.0};

static float x3[][N_INDEPENDENT] = {-3.0,-1.0, 3.0,

2.0, 1.0, 1.0,

2.0, 1.0, 4.0};

static float y1[] = {7.0,-5.0, 6.0};

static float y2[] = {5.0, 5.0,-2.0};

static float y3[] = {0.0, 8.0, 3.0};

imsls_f_regression(N_OBSERVATIONS_BLOCK_1, N_INDEPENDENT, &x1[0][0], y1,

IMSLS_RETURN_USER, coefficients,

IMSLS_IDO, 1,

0);

imsls_f_regression(N_OBSERVATIONS_BLOCK_2, N_INDEPENDENT, &x2[0][0], y2,

IMSLS_RETURN_USER, coefficients,

IMSLS_IDO, 2,

0);

imsls_f_regression(N_OBSERVATIONS_BLOCK_3, N_INDEPENDENT, &x3[0][0], y3,

IMSLS_RETURN_USER, coefficients,

IMSLS_COEF_COVARIANCES, &coef_covariance,

IMSLS_X_MEAN, &x_mean,

IMSLS_IDO, 3,

0);

imsls_f_write_matrix("\nLeast Squares Coefficients", 1,

N_COEFFICIENTS, coefficients, 0);

if (coef_covariance){

imsls_f_write_matrix("\nCoefficient Covariance",

N_COEFFICIENTS, N_COEFFICIENTS, coef_covariance,

IMSLS_PRINT_UPPER,

0);

imsls_free(coef_covariance);

}

if (x_mean){

imsls_f_write_matrix("\nx means", 1, N_INDEPENDENT, x_mean, 0);

imsls_free(x_mean);

}

Output

Least Squares Coefficients

1 2 3 4

7.733 -0.200 2.333 -1.667

Coefficient Covariance

1 2 3 4

1 0.3951 -0.0120 0.0289 -0.0778

2 0.0160 -0.0200 -0.0000

3 0.0556 -0.0111

4 0.0222

x means

1 2 3

2 1 4

Warning Errors

IMSLS_RANK_DEFICIENT

The model is not full rank. There is not a unique least-squares solution.

Fatal Errors

IMSLS_BAD_IDO_6	“ido” = #. Initial allocations must be performed by invoking the function with “ido” = 1.
IMSLS_BAD_IDO_7	“ido” = #. A new analysis may not begin until the previous analysis is terminated by invoking the function with “ido” = 3.

Contact Support