Computes the matrix of sums of squares and crossproducts for the multivariate general linear hypothesis HβU = G given the regression fit.
Synopsis
#include <imsls.h>
float *imsls_f_hypothesis_scph (Imsls_f_regression *regression_info, int nh, float h[], float *dfh, ..., 0)
The type double function is imsls_d_hypothesis_scph.
Required Argument
Imsls_f_regression
*regression_info (Input)
Pointer to a
structure of type Imsls_f_regression containing information about the
regression fit. See function imsls_f_regression.
int nh
(Input)
Number of rows in the hypothesis matrix, h.
float h[]
(Input)
The H array of size nh by
n_coefficients with each row corresponding to a row in the hypothesis and
containing the constants that specify a linear combination of the
regression coefficients. Here, n_coefficients is the number of
coefficients in the fitted regression model.
float *dfh
(Output)
Degrees of freedom for the sums of squares and crossproducts matrix.
This is equal to the rank of input matrix h.
Return Value
Array of size nu by nu containing the sums of squares and crossproducts attributable to the hypothesis.
Synopsis with Optional Arguments
#include <imsls.h>
float
*imsls_f_regression_scph (Imsls_f_regression *regression_info,
int
nh,
float h[],
float *dfh,
IMSLS_G,
float
g[],
IMSLS_U,
int
nu,
float u[],
IMSLS_RETURN_USER,
scph[],
0)
Optional Arguments
IMSLS_G, float g[]
(Input)
Array of size nh by nu containing
the G matrix, the null hypothesis values. By default, each value of
G is equal to 0.
IMSLS_U, int nu, float u[]
(Input)
Argument nu is the number of
linear combinations of the dependent variables to be considered. The value nu must be greater
than 0 and less than or equal to n_dependent.
Argument u contains the n_dependent by nu U matrix for the test HpβU = Gp.
Default: nu = n_dependent and u is the identity matrix
IMSLS_RETURN_USER, float scph[]
(Output)
If specified, the sums of squares and crossproducts matrix is stored
in array scph
provided by the user, where scph is of size nu by nu.
Description
Function imsls_f_hypothesis_scph computes the matrix of sums of squares and crossproducts for the general linear hypothesis HβU = G for the multivariate general linear model Y = Xβ + ɛ.
The rows of H must be linear combinations of the rows of R, i.e., Hβ = G must be completely testable. If the hypothesis is not completely testable, function imsls_f_hypothesis_partial can be used to construct an equivalent completely testable hypothesis.
Computations are based on an algorithm discussed by Kennedy and Gentle (1980, p. 317) that is extended by Sallas and Lionti (1988) for mulitvariate non-full rank models with possible linear equality restrictions. The algorithm is as follows:
1. Form 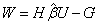 .
.
2. Find C as the solution of RTC = HT. If the equations are declared inconsistent within a computed tolerance, a warning error message is issued that the hypothesis is not completely testable.
3. For all rows of R corresponding to restrictions, i.e., containing negative diagonal elements from a restricted least-squares fit, zero out the corresponding rows of C, i.e., from DC.
4. Decompose DC using Householder transformations and column pivoting to yield a square, upper triangular matrix T with diagonal elements of nonincreasing magnitude and permutation matrix P such that
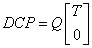
where Q is an orthogonal matrix.
5. Determine the rank of T, say r. If t11 = 0, then r = 0. Otherwise, the rank of T is r if
| trr | > | t11 | ɛ ≥ | tr + 1, r + 1 |
where ɛ = 10.0 × imsls_f_machine(4) (10.0 × imsls_d_machine(4) for the double-precision version).
Then, zero out all rows of T below r. Set the degrees of freedom for the hypothesis, dfh, to r.
6. Find V as a solution to TTV = PTW. If the equations are inconsistent, a warning error message is issued that the hypothesis is inconsistent within a computed tolerance, i.e., the linear system
HβU = G
Aβ = Z
does not have a solution for β.
Form VTV, which is the required matrix of sum of squares and crossproducts, scph.
In general, the two warning errors described above are serious user errors that require the user to correct the hypothesis before any meaningful sums of squares from this function can be computed. However, in some cases, the user may know the hypothesis is consistent and completely testable, but the checks in imsls_f_hypothesis_scph are too tight. For this reason, imsls_f_hypothesis_scph continues with the calculations.
Function imsls_f_hypothesis_scph gives a matrix of sums of squares and crossproducts that could also be obtained from separate fittings of the two models:
Y¹ = Xβ¹ + ɛ¹ (1)
Aβ¹ = Z¹
Hβ¹ = G
and
Y¹ = Xβ¹ + ɛ¹ (2)
Aβ¹ = Z¹
where Y¹ = YU, β¹ = βU, ɛ¹ = ɛU, and Z¹ = ZU. The error sum of squares and crossproducts matrix for (1) minus that for (2) is the matrix sum of squares and crossproducts output in scph. Note that this approach avoids the question of testability.
Example
The data for this example are from Maindonald (1984, pp. 203−204). A multivariate regression model containing two dependent variables and three independent variables is fit using function imsls_f_regression and the results stored in the structure info. The sum of squares and crossproducts matrix, scph, is then computed by calling imsls_f_hypothesis_scph for the test that the third independent variable is in the model (determined by the specification of h). The degrees of freedom for scph also is computed.
#include <imsls.h>
int main()
{
Imsls_f_regression *info;
float *coefficients, *scph;
float dfh;
float x[] = { 7.0, 5.0, 6.0,
2.0,-1.0, 6.0,
7.0, 3.0, 5.0,
-3.0, 1.0, 4.0,
2.0,-1.0, 0.0,
2.0, 1.0, 7.0,
-3.0,-1.0, 3.0,
2.0, 1.0, 1.0,
2.0, 1.0, 4.0 };
float y[] = { 7.0, 1.0,
-5.0, 4.0,
6.0, 10.0,
5.0, 5.0,
5.0, -2.0,
-2.0, 4.0,
0.0, -6.0,
8.0, 2.0,
3.0, 0.0 };
int n_observations = 9;
int n_independent = 3;
int n_dependent = 2;
int nh = 1;
float h[] = { 0, 0, 0, 1 };
coefficients = imsls_f_regression(n_observations, n_independent,
x, y,
IMSLS_N_DEPENDENT, n_dependent,
IMSLS_REGRESSION_INFO, &info,
0);
scph = imsls_f_hypothesis_scph(info, nh, h, &dfh, 0);
printf("Degrees of Freedom Hypothesis = %4.0f\n", dfh);
imsls_f_write_matrix("Sum of Squares and Crossproducts",
n_dependent, n_dependent, scph,
IMSLS_NO_COL_LABELS, IMSLS_NO_ROW_LABELS,
0);
}
Output
Degrees of Freedom Hypothesis = 1
Sum of Squares and Crossproducts
100 -40
-40 16
Warning Errors
IMSLS_HYP_NOT_TESTABLE The hypothesis is not completely testable within the computed tolerance. Each row of “h” must be a linear combination of the rows of “r”.
IMSLS_HYP_NOT_CONSISTENT The hypothesis is inconsistent within the computed tolerance.
