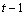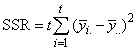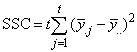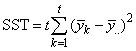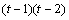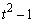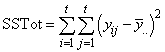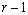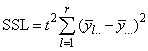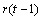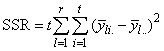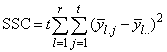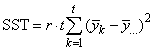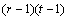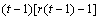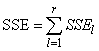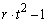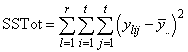Analyzes data from latin-square experiments. Function latin_square also analyzes latin-square experiments replicated at several locations.
Synopsis
#include <imsls.h>
float *imsls_f_latin_square (int n, int n_locations, int n_treatments, int row[], int col[], int treatment[], float y[], …, 0)
The type double function is imsls_d_latin_square.
Required Arguments
int n
(Input)
Number of missing and non-missing experimental observations.
imsls_f_latin_square
verifies that:
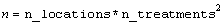
hint n_locations
(Input)
Number of locations. n_locations must be
one or greater. If n_locations>1 then
the optional array locations[] must be
included as input to imsls_f_latin_square.
int n_treatments
(Input)
Number of treatments. n_treatments must be
greater than one. In addition the number of rows and columns must be equal
to n_treatments.
int row[]
(Input)
An array of length n containing the row
identifiers for each observation in y. Each row must
be assigned values from 1 to n_treatments.
imsls_f_latin_square
verifies that the number of unique factor A identifiers is equal to n_treatments.
int col[]
(Input)
An array of length n containing the
column identifiers for each observation in y. Each column
must be assigned values from 1 to n_treatments.
imsls_f_latin_square
verifies that the number of unique column identifiers is equal to n_treatments.
int treatment[]
(Input)
An array of length n containing the
treatment identifiers for each observation in y. Each
treatment must be assigned values from 1 to n_treatments.
imsls_f_latin_square
verifies that the number of unique treatment identifiers is equal to n_treatments.
float y[] (Input)
An
array of length n containing the
experimental observations and any missing values. Missing values cannot be
omitted. They are indicated by placing a NaN (not a number) in y. The NaN value can be
set using either the function imsls_f_machine(6) or
imsls_d_machine((6),
depending upon whether single or double precision is being used,
respectively. The location, row, column, and treatment number for each
observation in y
are identified by the corresponding values in the arguments locations, row, col, and treatment.
Return Value
Address of a pointer to the memory location of a two dimensional, 7 by 6 array containing the ANOVA table. Each row in this array contains values for one of the effects in the ANOVA table. The first value in each row, anova_tablei,0 = anova_table[i*6], identifies the source for the effect associated with values in that row. The remaining values in a row contain the ANOVA table values using the following convention:
|
j |
anova_tablei,j = anova_table[i*6+j] |
|
0 |
Source Identifier (values described below) |
|
1 |
Degrees of freedom |
|
2 |
Sum of squares |
|
3 |
Mean squares |
|
4 |
F-statistic |
|
5 |
p-value for this F-statistic |
Note that the p-value for the F-statistic is returned as 0.0 when the value is so small that all significant digits have been lost.
The Source Identifiers in the first column of anova_tablei,j are the only negative values in anova_table[]. Assignments of identifiers to ANOVA sources use the following coding:
|
Source Identifier |
ANOVA Source |
|
-1 |
LOCATIONS † |
|
-2 |
ROWS |
|
-3 |
COLUMNS |
|
-4 |
TREATMENTS |
|
-5 |
LOCATIONS × TREATMENTS † |
|
-6 |
ERROR WITHIN LOCATIONS |
|
-7 |
CORRECTED TOTAL |
Note: † If n_locations=1 rows involving location are set to missing (NaN).
Synopsis with Optional Arguments
#include <imsl.h>
float
*imsls_f_latin_square (int
n, int
n_locations,
int n_treatments,
int row[],
int col[],
int treatment[], float y[],
IMSLS_RETURN_USER, float
anova_table[],
IMSLS_LOCATIONS, int
locations[],
IMSLS_N_MISSING,
int
*n_missing,
IMSLS_CV,
float *cv,
IMSLS_GRAND_MEAN,
float
*grand_mean,
IMSLS_TREATMENT_MEANS,
float
**treatment_means,
IMSLS_TREATMENT_MEANS_USER,
float
treatment_means[],
IMSLS_STD_ERRORS,
float
**std_err,
IMSLS_STD_ERRORS_USER,
float
std_err[],
IMSLS_LOCATION_ANOVA_TABLE,
float
**location_anova_table,
IMSLS_LOCATION_ANOVA_TABLE_USER,
float
location_anova_table[],
IMSLS_ANOVA_ROW_LABELS,
char
***anova_row_labels,
IMSLS_ANOVA_ROW_LABELS_USER,
char
*anova_row_labels[],
0)
Optional Arguments
IMSLS_RETURN_USER,
float anova_table[]
(Output)
User defined array of length 42 for storage of the 7 by
6 anova table described as the return argument for this function. For a
detailed description of the format for this table, see the previous description
of the return arguments for imsls_f_latin_square.
IMSLS_LOCATIONS,
int locations[]
(Input)
An array of length n containing the
location identifiers for each observation in y. Unique
integers must be assigned to each location in the study. This argument is
required when n_locations>1.
IMSLS_N_MISSING,
int *n_missing
(Output)
Number of missing values, if any, found in y. Missing
values are denoted with a NaN (Not a Number) value.
IMSLS_CV, float
*cv
(Output)
The coefficient of variation computed by using the within location
standard deviation.
IMSLS_GRAND_MEAN,
float *grand_mean
(Output)
Mean of all the data across every location.
IMSLS_TREATMENT_MEANS,
float **treatment_means
(Output)
Address of a pointer to an internally allocated array of
size n_treatments
containing the treatment means.
IMSLS_TREATMENT_MEANS_USER,
float treatment_means[]
(Output)
Storage for the array treatment_means,
provided by the user.
IMSLS_STD_ERRORS,
float **std_err
(Output)
Address of a pointer to an internally allocated array of
length 2 containing the standard error and associated degrees of freedom
for comparing two treatment means. std_err[0] contains the
standard error and its degrees of freedom are returned in std_err[1].
IMSLS_STD_ERRORS_USER,
float std_err[]
(Output)
Storage for the array std_err, provided by
the user.
IMSLS_LOCATION_ANOVA_TABLE,
float **location_anova_table
(Output)
Address of a pointer to an internally allocated 3-dimensional array
of size n_locations by 7 by 6
containing the anova tables associated with each location. For each
location, the 7 by 6 dimensional array corresponds to the anova table for that
location. For example, location_anova_table[(i-1)×42+(j-1)×6 + (k-1)] contains the value
in the k-th column and
j-th
row of the anova-table for the i-th location.
IMSLS_LOCATION_ANOVA_TABLE_USER, float anova_table[] (Output)
Storage for the array location_anova_table, provided by the user.
IMSLS_ANOVA_ROW_LABELS,
char ***anova_row_labels
(Output)
Address of a pointer to a pointer to an internally allocated array
containing the labels for each of the n_anova rows of the
returned ANOVA table. The label for the i-th row of the
ANOVA table can be printed with printf("%s", anova_row_labels[i]).
The
memory associated with anova_row_labels
can be freed with a single call to imsls_free(anova_row_labels).
IMSLS_ANOVA_ROW_LABELS_USER,
char *anova_row_labels[]
(Output)
Storage for the array anova_row_labels,
provided by the user. The amount of space required will vary depending
upon the number of factors and n_anova. An
upperbound on the required memory is char *anova_row_labels[600].
Description
The function imsls_f_latin_square analyzes latin-square experiments, possibly replicated at multiple locations. Latin-square experiments block treatments using two factors: rows and columns. The number of levels associated with rows and columns must equal the number of treatments. Treatments are blocked by rows and columns in a balanced arrangement to ensure that every row contain one replicate of every treatment. The same balance is required for every column, see Table 1. Notice that the four treatments, T1, T2, T3, and T4, appear exactly once in every column and every row.
|
|
|
Columns | |||
|
|
|
C1 |
C2 |
C3 |
C4 |
|
Rows |
R1 |
T1 |
T2 |
T3 |
T4 |
|
R2 |
T2 |
T3 |
T4 |
T1 | |
|
R3 |
T3 |
T4 |
T1 |
T2 | |
|
R4 |
T4 |
T1 |
T2 |
T3 | |
Table 4- 17 - Latin-Square Experiment with Four Treatments
A necessary assumption in Latin-Square experiments is that there are no interactions between treatments and the row and column blocking factors. For data collected at a single location, the Anova table for a Latin-Square experiment is usually organized into five rows, see Table 2.
|
Source |
DF |
Sum of Squares |
Mean Squares |
|
ROWS |
|
|
MSR |
|
COLUMNS |
|
|
MSC |
|
TREATMENTS |
|
|
MST |
|
ERROR |
|
SSE=SSTot-SSR-SSC-SST |
MSE |
|
TOTAL |
|
| |
Table 4- 18 – The ANOVA Table for a Latin-Square Experiment at one Location
The statistical model used to represent data is from a single location:
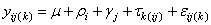 ,
,
where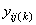 is the observation for the
k-th
treatment in the i-th row and
j-th
column of the Latin Square, and,
is the observation for the
k-th
treatment in the i-th row and
j-th
column of the Latin Square, and,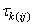 is the effect associated with
the k-th
treatment.
is the effect associated with
the k-th
treatment.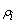 and
and 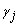 are the i-th row and
j-th
column effects, respectively, and
are the i-th row and
j-th
column effects, respectively, and 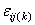 is the noise associated with this
observation.
is the noise associated with this
observation.
If multiple locations are involved, imsls_f_latin_square assumes that treatments are crossed with locations, but that row and column effects are nested within locations, see Table 3. The statistical model used to represent these data is:
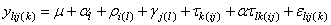 ,
,
where
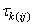
is the effect associated with the kth treatment, and
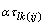
is the interaction effect between location l and treatment k.
|
SOURCE |
DF |
Sum of Squares |
Mean Squares |
|
LOCATIONS |
|
|
MSL |
|
ROWS |
|
|
MSR |
|
COLUMNS |
|
|
MSC |
|
TREATMENTS |
|
|
MST |
|
LOCATIONS X TREATMENTS |
|
SSLT by difference |
MSLT |
|
ERROR |
|
|
MSE |
|
TOTAL |
|
|
|
Table 4- 19 – The ANOVA Table for a Latin-Square Experiment at Multiple Locations
Example
This example uses four treatments organized into a latin square. This example also uses the function l_print_LSD(), which is defined in the first example for imsls_f_lattice().
#include <math.h>
#include <imsls.h>
#include <stdio.h>
#include <stdlib.h>
void l_print_LSD(int n1, int* equalMeans, float *means);
int main()
{
char **anova_row_labels;
char *col_labels[] = {" ", "\nID", "\nDF", "\nSSQ ",
"Mean \nsquares", "\nF-Test", "\np-Value"};
int i, l, page_width=100;
int n = 16; /* Total number of observations */
int n_treatments = 4;
int n_locations = 1;
int df, *equal_means;
float grand_mean, cv;
float *aov, *treatment_means, *std_err;
int col[]={1, 2, 3, 4, 1, 2, 3, 4, 1, 2, 3, 4, 1, 2, 3, 4};
int row[]={3, 2, 4, 1, 1, 4, 2, 3, 2, 3, 1, 4, 4, 1, 3, 2};
int treatment[]={1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4};
float alpha = 0.05;
float y[]={
1.167, 1.185, 1.655, 1.345, 1.64, 1.29, 1.665, 1.29,
1.475, 0.71, 1.425, 0.66, 1.565, 1.29, 1.4, 1.18
};
printf("\n\n*** Experimental Design ***");
printf("\n===============================");
printf("\n| COL | 1 | 2 | 3 | 4 |");
printf("\n===============================");
printf("\n|ROW 1 | 2 | 4 | 3 | 1 |");
printf("\n===============================");
printf("\n|ROW 2 | 3 | 1 | 2 | 4 |");
printf("\n===============================");
printf("\n|ROW 3 | 1 | 3 | 4 | 2 |");
printf("\n===============================");
printf("\n|ROW 4 | 4 | 2 | 1 | 3 |");
printf("\n===============================");
aov = imsls_f_latin_square(n, n_locations, n_treatments,
row, col, treatment, y,
IMSLS_GRAND_MEAN, &grand_mean,
IMSLS_CV, &cv,
IMSLS_TREATMENT_MEANS, &treatment_means,
IMSLS_STD_ERRORS, &std_err,
IMSLS_ANOVA_ROW_LABELS, &anova_row_labels,
0);
/* Print ANOVA table. */
imsls_page(IMSLS_SET_PAGE_WIDTH, &page_width);
imsls_f_write_matrix("\n *** ANALYSIS OF VARIANCE TABLE ***",
7, 6, aov,
IMSLS_WRITE_FORMAT, "%3.0f%3.0f%8.3f%8.3f%8.3f%8.3f",
IMSLS_ROW_LABELS, anova_row_labels,
IMSLS_COL_LABELS, col_labels,
0);
printf("\n\nGrand Mean: %7.3f", grand_mean);
printf("\n\nCoefficient of Variation: %7.3f\n\n", cv);
l = 0;
printf("Treatment Means: \n");
for (i=0; i < n_treatments; i++){
printf("treatment[%2d] %7.4f \n", i+1,
treatment_means[l++]);
}
df = (int)std_err[1];
printf("\n\n");
printf("Standard Error for Comparing Two Treatment Means: %f \n",
std_err[0]);
printf("(df=%d)\n", df);
equal_means = imsls_f_multiple_comparisons(n_treatments,
treatment_means, df, std_err[0]/sqrt(2.0),
IMSLS_LSD,
IMSLS_ALPHA, alpha,
0);
l_print_LSD(n_treatments, equal_means, treatment_means);
}
Output
*** Experimental Design ***
===============================
| COL | 1 | 2 | 3 | 4 |
===============================
|ROW 1 | 2 | 4 | 3 | 1 |
===============================
|ROW 2 | 3 | 1 | 2 | 4 |
===============================
|ROW 3 | 1 | 3 | 4 | 2 |
===============================
|ROW 4 | 4 | 2 | 1 | 3 |
===============================
*** ANALYSIS OF VARIANCE TABLE ***
Mean
ID DF SSQ squares F-Test p-Value
Locations ............. -1 ... ........ ........ ........ ........
Rows ................. -2 3 0.185 0.062 2.064 0.207
Columns ............... -3 3 0.589 0.196 6.579 0.025
Treatments ............ -4 3 0.352 0.117 3.927 0.073
Locations x Treatments -5 ... ........ ........ ........ ........
Error within Locations -6 6 0.179 0.030 ........ ........
Corrected Total ....... -7 15 1.305 ........ ........ ........
Grand Mean: 1.309
Coefficient of Variation: 13.204
Treatment Means:
treatment[ 1] 1.3380
treatment[ 2] 1.4712
treatment[ 3] 1.0675
treatment[ 4] 1.3587
Standard Error for Comparing Two Treatment Means: 0.122200
(df=6)
[group] Mean LSD Grouping
[3] 1.067500 *
[1] 1.338000 * *
[4] 1.358750 * *
[2] 1.471250 *