Predict a binomial or multinomial outcome given an estimated model and new values of the independent variables.
Synopsis
#include <imsls.h>
float *imsls_f_logistic_reg_predict (int n_observations, int n_independent, int n_classes, float coefs[], float x[],..., 0)
The type double function is imsls_d_logistic_reg_predict.
Required Arguments
int
n_observations (Input)
The number of observations.
int
n_independent (Input)
The number of independent
variables.
int n_classes
(Input)
The number of discrete outcomes, or classes.
float coefs[]
(Input)
Array of length n_coefficients × n_classes containing
the coefficient estimates of the logistic regression model. n_coefficients is the
number of coefficients in the model.
float x[] (Input)
Array of length n_observations × n_independent
containing the values of the independent variables.
Return Value
Pointer to an array containing the predicted responses. The predicted value is the predicted number of outcomes in each class for each new observation provided in x. If frequencies[i] = 1 for all observations, then the return value is equivalent to the predicted probabilities. If the option IMSLS_CONFIDENCE is specified, the length of the return array is (n_observations × n_classes × 3) and the array includes the lower and upper prediction limits. Otherwise, the array is of length (n_observations × n_classes). Note that if the data is column-oriented (see IMSLS_COLUMN_WISE), the return value will also be column-oriented.
Synopsis with Optional Arguments
#include <imsls.h>
float
*imsls_f_logistic_reg_predict (int n_observations,
int n_independent, int n_classes,
float coefs[],
float x[],
IMSLS_Y,
float
y[],
IMSLS_GROUP_COUNTS,
or
IMSLS_GROUPS,
IMSLS_COLUMN_WISE,
IMSLS_FREQUENCIES,
int
frequencies[],
IMSLS_REFERENCE_CLASS,
int
ref_class,
IMSLS_NO_INTERCEPT,
IMSLS_X_INDICES,
int
n_xin,
int xin[],
IMSLS_X_INTERACTIONS,
int
n_xinteract,
int
xinteract[],
IMSLS_CONFIDENCE,
float
confid.
IMSLS_MODEL,
Imsls_f_model
*model,
IMSLS_PREDERR,
float
*prederr,
IMSLS_RETURN_USER,
float
yhat[],
0)
Optional Arguments
IMSLS_Y, float
y[]
(Input)
Array containing the actual responses corresponding to the
independent variables. If present, the expected length for y is n_observations × n_classes unless one
of IMSLS_GROUPS
or IMSLS_GROUP_COUNTS is
also present. IMSLS_Y is required
when IMSLS_PREDERR is
requested.
Default: The function expects that y is not given.
IMSLS_GROUP_COUNTS or
IMSLS_GROUPS,
(Input)
These optional arguments specify alternative formats of the
input array y. If IMSLS_GROUP_COUNTS is
present, y is of
length n_observations × (n_classes - 1), and
contains counts for all but one of the classes for each observation. The
missing class is treated as the reference class. If IMSLS_GROUP_COUNTS is
present and if any y[i] > 1,
IMSLS_FREQUENCIES is
required. If IMSLS_GROUPS is
present, the input array y is of length n_observations and
y[i] contains
the group number to which the i-th
observation belongs. In this case, frequencies[i] is set
to 1 for all observations.
Default: Unless one of the arguments is present,
the function expects that y is n_observations × n_classes and contains
counts for all the classes.
IMSLS_COLUMN_WISE,
(Input)
If present, the input arrays are column-oriented.
That is, contiguous elements in x are values of the
same independent variable, or column, except at multiples of n_observations.
Default:
Input arrays are row-oriented.
IMSLS_FREQUENCIES,
int frequencies[]
(Input)
Array of length n_observations
containing the number of replications or trials for each of the
observations. This argument is required if IMSLS_GROUP_COUNTS is
present and if any y[i] > 1.
Default: frequencies[i] =
1.
IMSLS_REFERENCE_CLASS,
int ref_class
(Input)
Number specifying which class or outcome category to use as the
reference class. The purpose of the reference class is explained in the Description
section.
Default: ref_class = n_classes.
IMSLS_NO_INTERCEPT
(Input)
If present, the model will not include an intercept
term.
Default: The intercept term is included.
IMSLS_X_INDICES,
int n_xin, int
xin[]
(Input)
An array of length n_xin providing the
variable indices of x that correspond to
the independent variables the user wishes to be included in the logistic
regression model.
Default: All n_independent
variables are included.
IMSLS_X_INTERACTIONS,
int n_xinteract,
int xinteract[]
(Input)
An array of length n_xinteract × 2
providing pairs of variable indices of x that define the
interaction terms in the model. Adjacent indices should be
unique.
Default: No interaction terms are included.
IMSLS_CONFIDENCE,
float confid
(Input)
This value provides the confidence level to use in the
calculation of the prediction intervals. If this argument is present and
valid (0 < confid < 100), confid% prediction
intervals are provided for each predicted value.
Default: Prediction
intervals are not provided.
IMSLS_MODEL,
Imsls_f_model *model
(Input)
Pointer to a structure of type Imsls_f_model
containing information about the logistic regression fit. See imsls_f_logistic_regression.
Required when IMSLS_CONFIDENCE is
present.
Default: Not needed if IMSLS_CONFIDENCE is
not present.
IMSLS_PREDERR,
float *prederr
(Output)
The mean squared prediction error when IMSLS_Y is
present.
IMSLS_RETURN_USER,
float yhat[]
(Output)
Storage for the return value is provided by the user.
See the description of the Return Value above for
details.
Description
Function imsls_f_logistic_reg_predict calculates the predicted outcomes for a binomial or multinomial response variable given an estimated logistic regression model and new observations of the independent variables.
For a binary response y, the objective is to
estimate the conditional probability of success,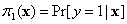 
, where 
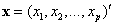is a realization of p
independent variables. In particular, the estimated probability of
success
,
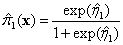where
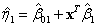
and
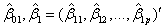are the coefficient
estimates. Then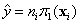 
. That is, 
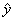is the expected value of the
response under the estimated model given the values of the independent
variables.
Similarly, for a multinomial response, with class K the reference class,
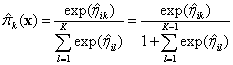
Then
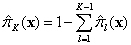
and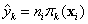
. If the actual responses are given,
the mean squared prediction error is
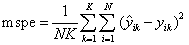
If requested,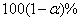
prediction intervals are provided for
the predicted values by first finding the prediction standard errors of the
logits,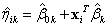 
, and then evaluating
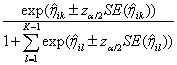
to obtain the upper and lower limits for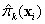 
, where 
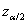is the upper 
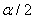quantile of the standard normal
distribution. Note that properties of the prediction intervals are only
valid when the new observations are inside the range of the original data used
to fit the model. Generally, the model should not be used to extrapolate outside
the range of the original data. See Hosmer and Lemeshow (2000) for further
details.
Examples
Example 1
The model fit to the beetle mortality data of Prentice (1976) is used to predict the expected mortality at three new doses. For the original data, see Example 1 in imsls_f_logistic_regression.
|
Log Dosage |
Number of Beetles Exposed |
Number of Deaths |
|
1.66 |
16 |
?? |
|
1.87 |
22 |
?? |
|
1.71 |
11 |
?? |
#include <imsls.h>
#include <stdio.h>
int main(){
float y1[8]={6, 13, 18, 28, 52, 53, 61, 60};
float x1[8]={1.69, 1.724, 1.755, 1.784, 1.811, 1.836, 1.861, 1.883};
float x2[3]={1.66, 1.87, 1.71};
float freqs1[8]={59, 60, 62, 56, 63, 59, 62, 60};
float freqs2[3]={16, 22, 11};
float *coefs, *yhat;
int n_classes=2, n_observations=8, n_independent=1,
n_coefs=2, i,n_new_observations=3;
coefs=imsls_f_logistic_regression(n_observations,n_independent,
n_classes,x1,y1,
IMSLS_GROUP_COUNTS,
IMSLS_FREQUENCIES,freqs1,
0);
imsls_f_write_matrix("Coefficient Estimates",(n_coefs)*(n_classes-1),
1,coefs,0);
yhat=imsls_f_logistic_reg_predict(n_new_observations,n_independent,
n_classes,coefs,x2,IMSLS_FREQUENCIES,freqs2,0);
printf( "\nDose\t N\tExpected Deaths\n");
for(i=0;i<n_new_observations;i++){
printf("%5.2f\t%2.1f\t\t%5.2f\n",
x2[i],freqs2[i],yhat[2*i]);
}
}
Output
Coefficient Estimates
1 -60.76
2 34.30
Dose N Expected Deaths
1.66 16.0 0.34
1.87 22.0 21.28
1.71 11.0 1.19
Example 2
A logistic regression model is fit to artificial (noisy) data with 4 classes and 3 independent variables and used to predict class probabilities at 10 new values of the independent variables. Also shown are the mean squared prediction error and upper and lower limits of the 95% prediction interval for each predicted value.
#include <imsls.h>
#include <stdio.h>
int main(){
float x[50*3]={
3, 2, 2, 1, 3, 3, 3, 2, 3, 3, 3, 3, 3, 3, 2, 3, 2, 1, 3, 2,
2, 1, 2, 1, 3, 2, 1, 2, 1, 2, 3, 2, 1, 2, 1, 1, 2, 3, 1, 2,
1, 1, 1, 3, 1, 3, 2, 3, 3, 1,
25.92869, 51.63245, 25.78432, 39.37948, 24.65058, 45.20084,
52.6796, 44.28342, 40.63523, 51.76094, 26.30368, 20.70230,
38.74273, 19.47333, 26.42211, 37.05986, 51.67043, 42.40156,
33.90027, 35.43282, 44.30369, 46.72387, 46.99262, 36.05923,
36.83197, 61.66257, 25.67714, 39.08567, 48.84341, 39.34391,
24.73522, 50.55251, 31.34263, 27.15795, 31.72685, 25.00408,
26.35457, 38.12343, 49.9403, 42.45779, 38.80948, 43.22799,
41.87624, 48.0782, 43.23673, 39.41294, 23.93346,
42.8413, 30.40669, 37.77389,
1, 2, 1, 1, 1, 1, 2, 2, 2, 1, 1, 2, 2, 1, 1, 2, 2, 1, 2, 1, 1,
1, 1, 1, 2, 2, 1, 2, 2, 1, 1, 2, 2, 2, 1, 1, 2, 1, 1, 2, 2, 2,
1, 1, 2, 1, 1, 2, 1, 1
};
float y[50]={
1, 2, 3, 4, 3, 3, 4, 4, 4, 4, 2, 1, 4, 1, 1, 1, 4, 4, 3, 1, 2,
3, 3, 4, 2, 3, 4, 1, 2, 4, 3, 4, 4, 1, 3, 4, 4, 2, 3, 4, 2, 2,
4, 3, 1, 4, 3, 4, 2, 3
};
float newx[10*3]={
2, 2, 1, 3, 3, 3, 2, 3, 3, 3,
25.92869, 51.63245, 25.78432, 39.37948, 24.65058, 45.20084,
52.6796, 44.28342, 40.63523, 51.76094,
1, 2, 1, 1, 1, 1, 2, 2, 2, 1
};
float newy[10]={
3, 2, 1, 1, 4, 3, 2, 2, 1, 2
};
float *coefs,*yhat,mspe,model_pval,lrstat;
int i,j,n_classes,n_observations,n_new_obs,n_independent,n_coefs,dof;
Imsls_f_model *model_info_ptr=NULL;
n_classes=4;
n_observations=50;
n_new_obs=10;
n_independent=3;
n_coefs=4;
coefs=imsls_f_logistic_regression(n_observations,n_independent,
n_classes,x,y,
IMSLS_GROUPS,
IMSLS_COLUMN_WISE,
IMSLS_LRSTAT,&lrstat,
IMSLS_NEXT_RESULTS,&model_info_ptr,
0);
yhat=imsls_f_logistic_reg_predict(n_new_obs,n_independent,
n_classes,coefs,newx,
IMSLS_Y,newy,
IMSLS_GROUPS,
IMSLS_COLUMN_WISE,
IMSLS_CONFIDENCE,95.0,
IMSLS_MODEL,model_info_ptr,
IMSLS_PREDERR,&mspe,
0);
dof = n_coefs*(n_classes-1) - (n_classes-1);
model_pval = 1.0 -
imsls_f_chi_squared_cdf(lrstat,dof);
printf("Model Fit Summary:\n");
printf("Log-likelihood: %5.2f \n",model_info_ptr->loglike);
printf("LR test statistic: %5.2f\n",lrstat);
printf("Degrees of freedom: %d\n", dof);
printf("P-value: %5.4f\n", model_pval);
printf("\nPrediction Summary:\n");
printf("Mean squared prediction error: %4.2f\n", mspe);
printf("\n%Obs Class Estimate Lower Upper\n");
for(j=0;j<n_new_obs;j++){
for(i=0;i<n_classes;i++){
printf(" %d\t%d %4.2f %4.2f %4.2f\n",j+1,i+1,
yhat[i*3*n_new_obs+j],
yhat[(i*3+1)*n_new_obs+j],
yhat[(i*3+2)*n_new_obs+j]);
}
}
}
Output
Model Fit Summary:
Log-likelihood: -58.58
LR test statistic: 16.37
Degrees of freedom: 9
P-value: 0.0595
Prediction Summary:
Mean squared prediction error: 0.21
Obs Class Estimate Lower Upper
1 1 0.26 0.20 0.20
1 2 0.14 0.11 0.11
1 3 0.31 0.24 0.24
1 4 0.29 0.45 0.46
2 1 0.04 0.03 0.03
2 2 0.27 0.17 0.17
2 3 0.12 0.08 0.08
2 4 0.57 0.72 0.72
3 1 0.23 0.17 0.17
3 2 0.13 0.10 0.10
3 3 0.28 0.21 0.21
3 4 0.36 0.52 0.53
4 1 0.06 0.04 0.05
4 2 0.16 0.13 0.13
4 3 0.49 0.38 0.38
4 4 0.29 0.45 0.45
5 1 0.34 0.28 0.28
5 2 0.13 0.11 0.11
5 3 0.30 0.25 0.25
5 4 0.22 0.36 0.37
6 1 0.03 0.02 0.02
6 2 0.16 0.12 0.12
6 3 0.53 0.41 0.41
6 4 0.29 0.44 0.45
7 1 0.04 0.02 0.02
7 2 0.27 0.17 0.17
7 3 0.13 0.08 0.08
7 4 0.57 0.72 0.73
8 1 0.14 0.09 0.09
8 2 0.29 0.19 0.20
8 3 0.12 0.08 0.08
8 4 0.46 0.63 0.63
9 1 0.21 0.14 0.15
9 2 0.27 0.19 0.19
9 3 0.10 0.07 0.07
9 4 0.42 0.59 0.60
10 1 0.01 0.01 0.01
10 2 0.15 0.12 0.12
10 3 0.57 0.44 0.45
10 4 0.28 0.43 0.44
Warning Errors
|
IMSLS_NO_ACTUALS |
The average squared prediction error cannot be calculated because no actual “y” values are given. |
Fatal Errors
|
IMSLS_OVERFLOW |
The linear predictor = # is too large and will lead to overflow when exponentiated. |
*Relationship between the parameter, θ or λ, and a linear model of the explanatory variables, X β.
