Generates regressors for a general linear model.

Synopsis

#include <imsls.h>

int imsls_f_regressors_for_glm (int n_observations, float x[], int n_class, int n_continuous, ..., 0)

The type double function is imsls_d_regressors_for_glm.

Required Arguments

int n_observations   (Input)
Number of observations.

float x[]   (Input)
An n_observations × (n_class + n_continuous) array containing the data. The columns must be ordered such that the first n_class columns contain the class variables and the next n_continuous columns contain the continuous variables. (Exception: see optional argument IMSLS_X_CLASS_COLUMNS.)

int n_class   (Input)
Number of classification variables.

int n_continuous   (Input)
Number of continuous variables.

Return Value

An integer (n_regressors) indicating the number of regressors generated.

Synopsis with Optional Arguments

#include <imsls.h>

int imsls_f_regressors_for_glm (int n_observations, float x[], int n_class, int n_continuous,

IMSLS_X_COL_DIM, int x_col_dim,

IMSLS_X_CLASS_COLUMNS, int x_class_columns[],

IMSLS_MODEL_ORDER, int model_order, or

IMSLS_INDICES_EFFECTS, int n_effects, int n_var_effects[], int indices_effects[],

IMSLS_DUMMY, Imsls_dummy_method dummy_method,

IMSLS_REGRESSORS, float **regressors,

IMSLS_REGRESSORS_USER, float regressors[],

IMSLS_REGRESSORS_COL_DIM, int regressors_col_dim,

0)

Optional Arguments

IMSLS_X_COL_DIM, int x_col_dim   (Input)
Column dimension of x.
Default: x_col_dim = n_class + n_continuous

IMSLS_X_CLASS_COLUMNS, int x_class_columns[]   (Input)
Index array of length n_class containing the column numbers of x that are the classification variables. The sremaining variables are assumed to be continuous.
Default: x_class_columns = 0, 1, ..., n_class − 1

IMSLS_MODEL_ORDER, int model_order   (Input)
Order of the model. Model order can be specified as 1 or 2. Use optional argument IMSLS_INDICES_EFFECTS to specify more complicated models.
Default: model_order = 1

     or

IMSLS_INDICES_EFFECTS, int n_effects, int n_var_effects[], int indices_effects[]   (Input)
Variable n_effects is the number of effects (sources of variation) in the model. Variable n_var_effects is an array of length n_effects containing the number of variables associated with each effect in the model. Argument indices_effects is an index array of length n_var_effects[0] + n_var_effects[1]+…+n_var_effects(n_effects − 1). The first n_var_effects[0] elements give the column numbers of x for each variable in the first effect. The next n_var_effects[1] elements give the column numbers for each variable in the second effect.  The last n_var_effects [n_effects − 1] elements give the column numbers for each variable in the last effect.

IMSLS_DUMMY, Imsls_dummy_method dummy_method   (Input)
Dummy variable option. Indicator variables are defined for each class variable as described in the “Description” section.

            Dummy variables are then generated from the n indicator variables in one of the following three ways:

dummy_method	Method
IMSLS_ALL	The n indicator variables are the dummy variables (default).
IMSLS_LEAVE_OUT_LAST	The dummies are the first n − 1 indicator variables.
IMSLS_SUM_TO_ZERO	The n − 1 dummies are defined in terms of the indicator variables so that for balanced data, the usual summation restrictions are imposed on the regression coefficients.

IMSLS_REGRESSORS, float **regressors   (Output)
Address of a pointer to the internally allocated array of size n_observations × n_regressors containing the regressor variables generated from x.

IMSLS_REGRESSORS_USER, float regressors[]   (Output)
Storage for array regressors is provided by the user. See IMSLS_REGRESSORS.

IMSLS_REGRESSORS_COL_DIM, int regressors_col_dim   (Input)
Column dimension of regressors.
Default: regressors_col_dim = n_regressors

Description

Function imsls_f_regressors_for_glm generates regressors for a general linear model from a data matrix. The data matrix can contain classification variables as well as continuous variables. Regressors for effects composed solely of continuous variables are generated as powers and crossproducts. Consider a data matrix containing continuous variables as Columns 3 and 4. The effect indices (3, 3) generate a regressor whose i-th value is the square of the i-th value in Column 3. The effect indices (3, 4) generates a regressor whose i-th value is the product of the i-th value in Column 3 with the i-th value in Column 4.

Regressors for an effect (source of variation) composed of a single classification variable are generated using indicator variables. Let the classification variable A take on values a₁, a₂, ..., a_n. From this classification variable, imsls_f_regressors_for_glm creates n indicator variables. For k = 1, 2, ..., n, we have

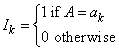
For each classification variable, another set of variables is created from the indicator variables. These new variables are called dummy variables. Dummy variables are generated from the indicator variables in one of three manners:

1.     The dummies are the n indicator variables.

2.     The dummies are the first n – 1 indicator variables.

3.     The n – 1 dummies are defined in terms of the indicator variables so that for balanced data, the usual summation restrictions are imposed on the regression coefficients.

In particular, for dummy_method = IMSLS_ALL, the dummy variables are A_k = I_k(k = 1, 2, ..., n). For dummy_method = IMSLS_LEAVE_OUT_LAST, the dummy variables are A_k = I_k(k = 1, 2, ..., n − 1). For dummy_method = IMSLS_SUM_TO_ZERO, the dummy variables are A_k = I_k − I_n(k = 1, 2, ..., n − 1). The regressors generated for an effect composed of a single-classification variable are the associated dummy variables.

Let m_j be the number of dummies generated for the j-th classification variable. Suppose there are two classification variables A and B with dummies

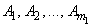
and

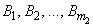
The regressors generated for an effect composed of two classification variables A and B are

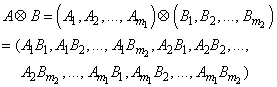
More generally, the regressors generated for an effect composed of several classification variables and several continuous variables are given by the Kronecker products of variables, where the order of the variables is specified in indices_effects. Consider a data matrix containing classification variables in Columns 0 and 1 and continuous variables in Columns 2 and 3. Label these four columns A, B, X₁, and X₂. The regressors generated by the effect indices (0, 1, 2, 2, 3) are A ⊗ B ⊗ X₁X₁X₂.

Remarks

Let the data matrix x = (A, B, X₁), where A and B are classification variables and X₁ is a continuous variable. The model containing the effects A, B, AB, X₁, AX₁, BX₁, and ABX₁ is specified as follows (use optional keyword IMSLS_INDICES_EFFECTS):

n_class = 2

n_continuous = 1

n_effects = 7

n_var_effects = (1, 1, 2, 1, 2, 2, 3)

indices_effects = (0, 1, 0, 1, 2, 0, 2, 1, 2, 0, 1, 2)

For this model, suppose that variable A has two levels, A₁ and A₂, and that variable B has three levels, B₁, B₂, and B₃. For each dummy_method option, the regressors in their order of appearance in regressors are given below.

 

dummy_method	regressors
IMSLS_ALL	A1, A2, B1, B2, B3, A1B1, A1B2, A1B3, A2B1, A2B2, A2B3, X1, A1X1, A2X1, B1X1, B2X1, B3X1, A1B1X1, A1B2X1, A1B3X1, A2B1X1, A2B2X1, A2B3X1
IMSLS_LEAVE_OUT_LAST	A1, B1, B2, A1B1, A1B2, X1, A1X1, B1X1, B2X1, A1B1X1, A1B2X1
IMSLS_SUM_TO_ZERO	A1 − A2, B1 − B3, B2 − B3, (A1 − A2) (B1 − B2), (A1 − A2) (B2 − B3), X1, (A1 − A2) X1,  (B1 − B3)X1, (B2 − B3)X1, (A1 − A2) (B1 − B2)X1, (A1  − A2) (B2 − B3)X1

 

Within a group of regressors corresponding to an interaction effect, the indicator variables composing the regressors vary most rapidly for the last classification variable, next most rapidly for the next to last classification variable, etc.

By default, imsls_f_regressors_for_glm internally generates values for n_effects, n_var_effects, and indices_effects, which correspond to a first order model with NEF = n_continuous + n_class. The variables then are used to create the regressor variables. The effects are ordered such that the first effect corresponds to the first column of x, the second effect corresponds to the second column of x, etc. A second order model corresponding to the columns (variables) of x is generated if IMSLS_MODEL_ORDER with model_order = 2 is specified.

There are

effects, where NVAR = n_continuous + n_class. The first NVAR effects correspond to the columns of x, such that the first effect corresponds to the first column of x, the second effect corresponds to the second column of x, ..., the NVAR-th effect corresponds to the NVAR-th column of x (i.e. x[NVAR − 1]). The next n_continuous effects correspond to squares of the continuous variables. The last

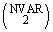
effects correspond to the two-variable interactions.

•      Let the data matrix x = (A, B, X₁), where A and B are classification variables and X₁ is a continuous variable. The effects generated and order of appearance is

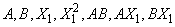
•      Let the data matrix x = (A, X₁, X₂), where A is a classification variable and X₁ and X₂ are continuous variables. The effects generated and order of appearance is

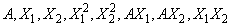
•      Let the data matrix x = (X₁, A, X₂) (see IMSLS_CLASS_COLUMNS), where A is a classification variable and X₁ and X₂ are continuous variables. The effects generated and order of appearance is

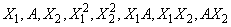
Higher-order and more complicated models can be specified using IMSLS_INDICES_EFFECTS.

Examples

Example 1

In the following example, there are two classification variables, A and B, with two and three values, respectively. Regressors for a one-way model (the default model order) are generated using the IMSLS_ALL dummy method (the default dummy method). The five regressors generated are A₁, A₂, B₁, B₂, and B₃.

 

#include <imsls.h>

 

int main() {

    int n_observations = 6;

    int n_class = 2;

    int n_cont  = 0;

    int n_regressors;

    float x[12] = {

        10.0,  5.0,

        20.0, 15.0,

        20.0, 10.0,

        10.0, 10.0,

        10.0, 15.0,

        20.0,  5.0};

 

   n_regressors = imsls_f_regressors_for_glm (n_observations, x,

       n_class, n_cont, 0);

 

   printf("Number of regressors = %3d\n", n_regressors);

}

Output

Number of regressors =   5

Example 2

In this example, a two-way analysis of covariance model containing all the interaction terms is fit. First, imsls_f_regressors_for_glm is called to produce a matrix of regressors, regressors, from the data x. Then, regressors is used as the input matrix into imsls_f_regression to produce the final fit. The regressors, generated using dummy_method = IMSLS_LEAVE_OUT_LAST, are the model whose mean function is

μ + α_i + β_j + Υ_ij + δx_ij + ζ_ix_ij + ηjx_ij + θ_ijx_ij   i = 1, 2; j = 1, 2, 3

where α₂ = β₃ = Υ₂₁ = Υ₂₂ = Υ₂₃ = ζ₂ = η₃ = θ₂₁ = θ₂₂ = θ₂₃ = 0.

 

#include <imsls.h>

 

int main() {

#define N_OBSERVATIONS 18

    int n_class = 2;

    int n_cont  = 1;

    float anova[15], *regressors;

    int n_regressors;

    float x[54] = {

        1.0, 1.0, 1.11,

        1.0, 1.0, 2.22,

        1.0, 1.0, 3.33,

        1.0, 2.0, 1.11,

        1.0, 2.0, 2.22,

        1.0, 2.0, 3.33,

        1.0, 3.0, 1.11,

        1.0, 3.0, 2.22,

        1.0, 3.0, 3.33,

        2.0, 1.0, 1.11,

        2.0, 1.0, 2.22,

        2.0, 1.0, 3.33,

        2.0, 2.0, 1.11,

        2.0, 2.0, 2.22,

        2.0, 2.0, 3.33,

        2.0, 3.0, 1.11,

        2.0, 3.0, 2.22,

        2.0, 3.0, 3.33};

   float y[N_OBSERVATIONS] = {

       1.0, 2.0, 2.0, 4.0, 4.0, 6.0,

       3.0, 3.5, 4.0, 4.5, 5.0, 5.5,

       2.0, 3.0, 4.0, 5.0, 6.0, 7.0};

   int class_col[2] = {0,1};

   int  n_effects = 7;

   int n_var_effects[7] = {1, 1, 2, 1, 2, 2, 3};

   int indices_effects[12] = {0, 1, 0, 1, 2, 0, 2, 1, 2, 0, 1, 2};

   float *coef;

   char      *reg_labels[] = {

        " ", "Alpha1", "Beta1", "Beta2", "Gamma11", "Gamma12",

        "Delta", "Zeta1", "Eta1", "Eta2", "Theta11", "Theta12"};

   char      *labels[] = {

        "degrees of freedom for the model",

        "degrees of freedom for error",

        "total (corrected) degrees of freedom",

        "sum of squares for the model",

        "sum of squares for error",

        "total (corrected) sum of squares",

        "model mean square", "error mean square",

        "F-statistic", "p-value",

        "R-squared (in percent)","adjusted R-squared (in percent)",

        "est. standard deviation of the model error",

        "overall mean of y",

        "coefficient of variation (in percent)"};

   n_regressors = imsls_f_regressors_for_glm (N_OBSERVATIONS, x,

       n_class, n_cont,

       IMSLS_X_CLASS_COLUMNS, class_col,

       IMSLS_DUMMY, IMSLS_LEAVE_OUT_LAST,

       IMSLS_INDICES_EFFECTS, n_effects, n_var_effects, indices_effects,

       IMSLS_REGRESSORS, &regressors,

       0);

 

   printf("Number of regressors = %3d", n_regressors);

 

   imsls_f_write_matrix ("regressors", N_OBSERVATIONS, n_regressors,

      regressors,

       IMSLS_COL_LABELS, reg_labels,

       0);

 

   coef = imsls_f_regression (N_OBSERVATIONS, n_regressors, regressors,

       y,

       IMSLS_ANOVA_TABLE_USER, anova,

       0);

 

   imsls_f_write_matrix ("* * * Analysis of Variance * * *\n", 15, 1,

        anova,

        IMSLS_ROW_LABELS,   labels,

        IMSLS_WRITE_FORMAT, "%11.4f",

        0);

 

}

Output

Number of regressors =  11

                                Regressors

        Alpha1       Beta1       Beta2     Gamma11     Gamma12       Delta

 1        1.00        1.00        0.00        1.00        0.00        1.11

 2        1.00        1.00        0.00        1.00        0.00        2.22

 3        1.00        1.00        0.00        1.00        0.00        3.33

 4        1.00        0.00        1.00        0.00        1.00        1.11

 5        1.00        0.00        1.00        0.00        1.00        2.22

 6        1.00        0.00        1.00        0.00        1.00        3.33

 7        1.00        0.00        0.00        0.00        0.00        1.11

 8        1.00        0.00        0.00        0.00        0.00        2.22

 9        1.00        0.00        0.00        0.00        0.00        3.33

10        0.00        1.00        0.00        0.00        0.00        1.11

11        0.00        1.00        0.00        0.00        0.00        2.22

12        0.00        1.00        0.00        0.00        0.00        3.33

13        0.00        0.00        1.00        0.00        0.00        1.11

14        0.00        0.00        1.00        0.00        0.00        2.22

15        0.00        0.00        1.00        0.00        0.00        3.33

16        0.00        0.00        0.00        0.00        0.00        1.11

17        0.00        0.00        0.00        0.00        0.00        2.22

18        0.00        0.00        0.00        0.00        0.00        3.33

 

         Zeta1        Eta1        Eta2     Theta11     Theta12

 1        1.11        1.11        0.00        1.11        0.00

 2        2.22        2.22        0.00        2.22        0.00

 3        3.33        3.33        0.00        3.33        0.00

 4        1.11        0.00        1.11        0.00        1.11

 5        2.22        0.00        2.22        0.00        2.22

 6        3.33        0.00        3.33        0.00        3.33

 7        1.11        0.00        0.00        0.00        0.00

 8        2.22        0.00        0.00        0.00        0.00

 9        3.33        0.00        0.00        0.00        0.00

10        0.00        1.11        0.00        0.00        0.00

11        0.00        2.22        0.00        0.00        0.00

12        0.00        3.33        0.00        0.00        0.00

13        0.00        0.00        1.11        0.00        0.00

14        0.00        0.00        2.22        0.00        0.00

15        0.00        0.00        3.33        0.00        0.00

16        0.00        0.00        0.00        0.00        0.00

17        0.00        0.00        0.00        0.00        0.00

18        0.00        0.00        0.00        0.00        0.00

 

 

           * * * Analysis of Variance * * *

 

degrees of freedom for the model                11.0000

degrees of freedom for error                     6.0000

total (corrected) degrees of freedom            17.0000

sum of squares for the model                    43.9028

sum of squares for error                         0.8333

total (corrected) sum of squares                44.7361

model mean square                                3.9912

error mean square                                0.1389

F-statistic                                     28.7364

p-value                                          0.0003

R-squared (in percent)                          98.1372

adjusted R-squared (in percent)                 94.7221

est. standard deviation of the model error       0.3727

overall mean of y                                3.9722

coefficient of variation (in percent)            9.3821

---

Contact Support