Chapter 8: Time Series and Forecasting > ts_outlier_identification

ts_outlier_identification

Detects and determines outliers and simultaneously estimates the model parameters in a time series whose underlying outlier free series follows a general seasonal or nonseasonal ARMA model.

Synopsis

#include <imsls.h>

float  *imsls_f_ts_outlier_identification (int n_obs, int model[],
float w[],…,0)

The type double function is imsls_d_ts_outlier_identification.

Required Arguments

int n_obs (Input)
Number of observations in the time series.

int model[] (Input)
Vector of length 4 containing the numbers p, q, s, d of the ARIMA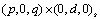 model the outlier free series is following.

float w[] (Input)
An array of length n_obs containing the time series.

Return Value

Pointer to an array of length n_obs containing the outlier free time series.
If an error occurred, NULL is returned.

Synopsis with Optional Arguments

#include <imsls.h>

float  *imsls_f_ts_outlier_identification (int n_obs,
int model[], float w[],
IMSLS_RETURN_USER, float x[],
IMSLS_DELTA, float delta,
IMSLS_CRITICAL, float critical,
IMSLS_EPSILON, float epsilon,
IMSLS_RELATIVE_ERROR, float relative_error,
IMSLS_RESIDUAL, float **residual,
IMSLS_RESIDUAL_USER, float residual[],
IMSLS_RESIDUAL_SIGMA, float *res_sigma,
IMSLS_NUM_OUTLIERS, int *num_outliers,
IMSLS_OUTLIER_STATISTICS, int **outlier_stat,
IMSLS_OUTLIER_STATISTICS_USER, int outlier_stat[],
IMSLS_TAU_STATISTICS, float **tau_stat,
IMSLS_TAU_STATISTICS_USER, float tau_stat[],
IMSLS_OMEGA_WEIGHTS, float **omega,
IMSLS_OMEGA_WEIGHTS_USER, float omega[],
IMSLS_ARMA_PARAM, float **parameters,
IMSLS_ARMA_PARAM_USER, float parameters[],
IMSLS_AIC, float *aic,
0)

Optional Arguments

IMSLS_RETURN_USER, float x[]  (Output)
A user supplied array of length n_obs containing the outlier free series.

IMSLS_DELTA, float delta (Input)
The dampening effect parameter used in the detection of a Temporary Change Outlier (TC), 0<delta < 1.
Default: delta = 0.7

IMSLS_CRITICAL, float critical  (Input)
Critical value used as a threshold for outlier detection, critical > 0.
Default: critical = 3.0

IMSLS_EPSILON, float epsilon  (Input)
Positive tolerance value controlling the accuracy of parameter estimates during outlier detection.
Default: epsilon = 0.001

IMSLS_RELATIVE_ERROR, float relative_error (Input)
Stopping criterion for the nonlinear equation solver used in function imsls_f_arma.
Default:  relative_error = .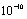

IMSLS_RESIDUAL, float **residual  (Output)
Address of a pointer to an internally allocated array of length n_obs containing the residuals for the outlier free series.

IMSLS_RESIDUAL_USER, float residual[]  (Output)
Storage for array residual is provided by the user. See IMSLS_RESIDUAL.

IMSLS_RESIDUAL_SIGMA, float *res_sigma  (Output)
Residual standard error of the outlier free series.

IMSLS_NUM_OUTLIERS, int *num_outliers  (Output)
The number of outliers detected.

IMSLS_OUTLIER_STATISTICS, int **outlier_stat  (Output)
Address of a pointer to an internally allocated array of length num_outliers × 2 containing  outlier statistics.  The first column contains the time at which the outlier was observed (t=1,2,...,n_obs) and the second column contains an identifier indicating the type of outlier observed. 
Outlier types fall into one of five categories:

0

Innovational Outliers (IO)

1

Additive outliers (AO)

2

Level Shift Outliers (LS)

3

Temporary Change Outliers (TC)

4

Unable to Identify (UI).

            Use IMSLS_NUM_OUTLIERS to obtain IMSLS_NUM_OUTLIERS, the number of detected outliers.
If num_outliers = 0, NULL is returned.

IMSLS_OUTLIER_STATISTICS_USER, int outlier_stat[]  (Output)
A user allocated array of length n_obs × 2 containing outlier statistics in the first num_outliers locations.  See IMSLS_OUTLIER_STATISTICS.
If num_outliers = 0, outlier_stat stays unchanged.

IMSLS_TAU_STATISTICS, float **tau_stat  (Output)
Address of a pointer to an internally allocated array of length num_outliers containing the t value for each detected outlier.
If num_outliers = 0, NULL is returned.

IMSLS_TAU_STATISTICS_USER, float tau_stat[] (Output)
A user allocated array of length n_obs containing the t value for each detected outlier in its first num_outliers locations.
If num_outliers = 0, tau_stat stays unchanged.

IMSLS_OMEGA_WEIGHTS, float **omega (Output)
Address of a pointer to an internally allocated array of length num_outliers containing the computed 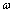weights for the detected outliers.
If num_outliers = 0, NULL is returned.

IMSLS_OMEGA_WEIGHTS_USER   float omega[] (Output)
A user allocated array of length n_obs containing the computed 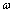weights for the detected outliers in its first num_outliers locations.
If num_outliers = 0, omega stays unchanged.

IMSLS_ARMA_PARAM,   float **parameters (Output)
Address of a pointer to an internally allocated array of length 1+p+q containing the estimated constant, AR and MA parameters.

IMSLS_ARMA_PARAM_USER   float parameters[] (Output)
A user allocated array of length 1+p+q containing the estimated constant, AR and MA parameters.

IMSLS_AIC, float   *aic (Output)
Akaike’s information criterion (AIC).

Description

Consider a univariate time series 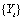that can be described by the following multiplicative seasonal ARIMA model of order :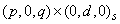

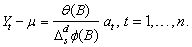
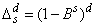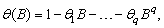
Here, ,  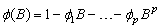.  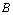is the lag operator, 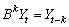,  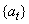is a white noise process, and 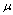 denotes the mean of the series .

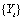In general, 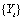 is not directly observable due to the influence of outliers. Chen and Liu (1993) distinguish between four types of outliers: innovational outliers (IO), additive outliers (AO), temporary changes (TC)  and level shifts (LS). If an outlier occurs as the last observation of the series, then Chen and Liu’s algorithm is unable to determine the outlier’s classification. In imsls_f_ts_outlier_identification, such an outlier is called a UI (unable to identify) and is treated as an innovational outlier.

In order to take the effects of multiple outliers occurring at time points 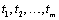 into account, Chen and Liu consider the following model:

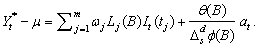
Here, 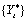 is the observed outlier contaminated series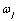, and  and 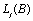 denote the magnitude and dynamic pattern of outlier 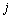, respectively.  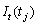 is an indicator function that determines the temporal course of the outlier effect, 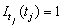,  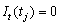otherwise. Note that 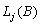 operates on  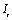via .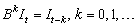

The last formula shows that the outlier free series 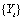 can be obtained from the original series 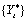 by removing all occurring outlier effects:

.

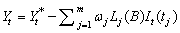The different types of outliers are charaterized by different values for: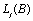

1. 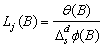  for an innovational outlier,

2. 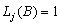  for an additive outlier,

3. 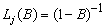  for a level shift outlier and

4. 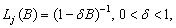  for a temporary change outlier.

Function imsls_f_ts_outlier_identification is an implementation of Chen and Liu’s algorithm. It determines the coefficients in 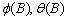 and the outlier effects in the model for the observed series jointly in three stages. The magnitude of the outlier effects is determined by least squares estimates. Outlier detection itself is realized by examination of the maximum value of the standardized statistics of the outlier effects. For a detailed description, see Chen and Liu’s original paper (1993).

Intermediate and final estimates for the coefficients in 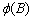 and 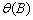 are computed by functions imsls_f_arma and imsls_f_max_arma.  If the roots of 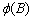or 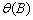 lie on or within the unit circle, then the algorithm stops with an appropriate error message. In this case, different values for p and q should be tried.

Examples

Example 1

This example is based on estimates of the Canadian lynx population. In order to simulate a measurement error, the actual time series value at time point 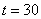, which is 0.25570e + 01, was replaced by 0.35570e + 01.  Function imsls_f_ts_outlier_identification is used to fit an AR(2) model of the form 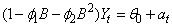, , 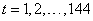 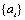Gaussian White noise, to the given series. Function imsls_f_ts_outlier_identification computes parameters 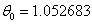,  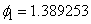and 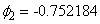 and identifies an additive outlier at time point .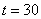

 

#include <imsls.h>

#include <stdio.h>

 

int main(){

    float series[114]={

    0.24300e+01,0.25060e+01,0.27670e+01,0.29400e+01,0.31690e+01,0.34500e+01,

    0.35940e+01,0.37740e+01,0.36950e+01,0.34110e+01,0.27180e+01,0.19910e+01,

    0.22650e+01,0.24460e+01,0.26120e+01,0.33590e+01,0.34290e+01,0.35330e+01,

    0.32610e+01,0.26120e+01,0.21790e+01,0.16530e+01,0.18320e+01,0.23280e+01,

    0.27370e+01,0.30140e+01,0.33280e+01,0.34040e+01,0.29810e+01,0.25570e+01,

    0.25760e+01,0.23520e+01,0.25560e+01,0.28640e+01,0.32140e+01,0.34350e+01,

    0.34580e+01,0.33260e+01,0.28350e+01,0.24760e+01,0.23730e+01,0.23890e+01,

    0.27420e+01,0.32100e+01,0.35200e+01,0.38280e+01,0.36280e+01,0.28370e+01,

    0.24060e+01,0.26750e+01,0.25540e+01,0.28940e+01,0.32020e+01,0.32240e+01,

    0.33520e+01,0.31540e+01,0.28780e+01,0.24760e+01,0.23030e+01,0.23600e+01,

    0.26710e+01,0.28670e+01,0.33100e+01,0.34490e+01,0.36460e+01,0.34000e+01,

    0.25900e+01,0.18630e+01,0.15810e+01,0.16900e+01,0.17710e+01,0.22740e+01,

    0.25760e+01,0.31110e+01,0.36050e+01,0.35430e+01,0.27690e+01,0.20210e+01,

    0.21850e+01,0.25880e+01,0.28800e+01,0.31150e+01,0.35400e+01,0.38450e+01,

    0.38000e+01,0.35790e+01,0.32640e+01,0.25380e+01,0.25820e+01,0.29070e+01,

    0.31420e+01,0.34330e+01,0.35800e+01,0.34900e+01,0.34750e+01,0.35790e+01,

    0.28290e+01,0.19090e+01,0.19030e+01,0.20330e+01,0.23600e+01,0.26010e+01,

    0.30540e+01,0.33860e+01,0.35530e+01,0.34680e+01,0.31870e+01,0.27230e+01,

    0.26860e+01,0.28210e+01,0.30000e+01,0.32010e+01,0.34240e+01,0.35310e+01

    };

   

    int i, model[4] = {2,0,1,0}, n_obs = 114;

    int *outlier_stat = NULL, num_outliers;

    float *parameters = NULL, *result = NULL;

    float res_sigma, aic;

   

    /* Simulate measurement error */

    series[29] = 0.35570e+01;

    result = imsls_f_ts_outlier_identification(n_obs, model, series,

        IMSLS_CRITICAL, 3.5,

        IMSLS_NUM_OUTLIERS, &num_outliers,

        IMSLS_OUTLIER_STATISTICS, &outlier_stat,

        IMSLS_ARMA_PARAM, &parameters,

        IMSLS_RESIDUAL_SIGMA, &res_sigma,

        IMSLS_AIC, &aic, 0);

 

    printf("\nARMA parameters:\n");

    for (i=0; i<=model[0]+model[1]; i++)

        printf("%d\t\t%lf\n", i, parameters[i]);

    printf("\nNumber of outliers: %d\n\n", num_outliers);

    printf("Outlier statistics:\n");

    printf("Time point\tOutlier type\n");

    for (i=0; i<num_outliers; i++)

        printf(" t=%2d\t\t   Type=%d\n", outlier_stat[2*i],

        outlier_stat[2*i+1]);

    printf("\n\nRSE: %lf\n", res_sigma);

    printf("AIC: %lf\n", aic);

    printf("\nExtract from the series:\n\n");

    printf ("time point    original series    outlier free series\n\n");

    for (i=0; i<36; i++)

        printf ("%2d %21.4f %21.4f\n", i+1, series[i], result[i]);

}

 

 

Output

 

ARMA parameters:

0               1.052683

1               1.389253

2               -0.752184

 

Number of outliers: 1

 

Outlier statistics:

Time point      Outlier type

 t=30              Type=1

 

RSE: 0.225020

AIC: 202.958511

 

Extract from the series:

 

time point    original series    outlier free series

 

 1                2.4300                2.4300

 2                2.5060                2.5060

 3                2.7670                2.7670

 4                2.9400                2.9400

 5                3.1690                3.1690

 6                3.4500                3.4500

 7                3.5940                3.5940

 8                3.7740                3.7740

 9                3.6950                3.6950

10                3.4110                3.4110

11                2.7180                2.7180

12                1.9910                1.9910

13                2.2650                2.2650

14                2.4460                2.4460

15                2.6120                2.6120

16                3.3590                3.3590

17                3.4290                3.4290

18                3.5330                3.5330

19                3.2610                3.2610

20                2.6120                2.6120

21                2.1790                2.1790

22                1.6530                1.6530

23                1.8320                1.8320

24                2.3280                2.3280

25                2.7370                2.7370

26                3.0140                3.0140

27                3.3280                3.3280

28                3.4040                3.4040

29                2.9810                2.9810

30                3.5570                2.7403

31                2.5760                2.5760

32                2.3520                2.3520

33                2.5560                2.5560

34                2.8640                2.8640

35                3.2140                3.2140

36                3.4350                3.4350

 

Example 2

This example is an artificial realization of an ARMA(1,1) process via formula 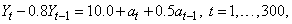 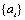Gaussian white noise, .

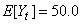An additive outlier with 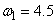 was added at time point 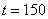, a temporary change outlier with 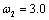 was added at time point .

 

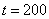#include <imsls.h>

#include <stdio.h>

 

int main()

{

  int i, n_obs = 300, num_outliers;

  int outlier_stat[300], model[4] = {1,1,1,0};

  float res_sigma, aic;

  float parameters[300], result[300], omega[300];

  float series[300]={

    50.0000000,50.2728081,50.6242599,51.0373917,51.9317627,50.3494759,

    51.6597252,52.7004929,53.5499802,53.1673279,50.2373505,49.3373871,

    49.5516472,48.6692696,47.6606636,46.8774185,45.7315445,45.6469727,

    45.9882355,45.5216560,46.0479660,48.1958656,48.6387749,49.9055367,

    49.8077278,47.7858467,47.9386749,49.7691956,48.5425873,49.1239853,

    49.8518791,50.3320694,50.9146347,51.8772049,51.8745689,52.3394470,

    52.7273712,51.4310036,50.6727448,50.8370399,51.2843437,51.8162918,

    51.6933670,49.7038231,49.0189247,49.455703,50.2718010,49.9605980,

    51.3775749,50.2285385,48.2692299,47.6495590,49.2938499,49.1924858,

    49.6449242,50.0446815,51.9972496,54.2576981,52.9835434,50.4193535,

    50.3617897,51.8276901,53.1239929,54.0682144,54.9238319,55.6877632,

    54.8896332,54.0701065,52.2754097,52.2522354,53.1248703,51.1287193,

    50.5003815,49.6504173,47.2453079,45.4555626,45.8449707,45.9765129,

    45.7682228,45.2343674,46.6496811,47.0894432,49.3368340,50.8058052,

    49.9132500,49.5893288,48.2470627,46.9779968,45.6760864,45.7070389,

    46.6158409,47.5303612,47.5630417,47.0389214,46.0352287,45.8161545,

    45.7974396,46.0015373,45.3796463,45.3461685,47.6444016,49.3327446,

    49.3810692,50.2027817,51.4567032,52.3986320,52.5819206,52.7721825,

    52.6919098,53.3274345,55.1345940,56.8962631,55.7791634,55.0616989,

    52.3551178,51.3264084,51.0968323,51.1980476,52.8001442,52.0545082,

    50.8742943,51.5150337,51.2242050,50.5033989,48.7760124,47.4179192,

    49.7319527,51.3320541,52.3918304,52.4140434,51.0845947,49.6485748,

    50.6893463,52.9840813,53.3246994,52.4568024,51.9196091,53.6683121,

    53.4555359,51.7755814,49.2915611,49.8755112,49.4546776,48.6171913,

    49.9643021,49.3766441,49.2551308,50.1021881,51.0769119,55.8328133,

    52.0212708,53.4930801,53.2147255,52.2356453,51.9648819,52.1816330,

    51.9898071,52.5623627,51.0717278,52.2431946,53.6943054,54.3752098,

    54.1492615,53.8523254,52.1093712,52.3982697,51.2405128,50.3018112,

    51.3819618,49.5479546,47.5024452,47.4447708,47.8939056,48.4070015,

    48.2440681,48.7389755,49.7309227,49.1998024,49.5798340,51.1196213,

    50.6288414,50.3971405,51.6084099,52.4564743,51.6443901,52.4080658,

    52.4643364,52.6257210,53.1604691,51.9309731,51.4137230,52.1233368,

    52.9867249,53.3180733,51.9647636,50.7947655,52.3815842,50.8353729,

    49.4136009,52.8355217,52.2234840,51.1392517,48.5245132,46.8700218,

    46.1607285,45.2324257,47.4157829,48.9989090,49.6230736,50.4352913,

    51.1652985,50.2588654,50.7820129,51.0448799,51.2880516,49.6898804,

    49.0288200,49.9338837,48.2214432,46.2103348,46.9550171,47.5595894,

    47.7176018,48.4502945,50.9816895,51.6950073,51.6973495,52.1941261,

    51.8988075,52.5617599,52.0218391,49.5236053,47.9684906,48.2445183,

    48.8275146,49.7176971,51.5649338,52.5627213,52.0182419,50.9688835,

    51.5846901,50.9486771,48.8685837,48.5600624,48.4760094,48.5348396,

    50.4187813,51.2542381,50.1872864,50.4407692,50.6222687,50.4972000,

    51.0036087,51.3367500,51.7368202,53.0463791,53.6261253,52.0728683,

    48.9740753,49.3280830,49.2733917,49.8519020,50.8562126,49.5594254,

    49.6109200,48.3785629,48.0026474,49.4874268,50.1596375,51.8059540,

    53.0288620,51.3321075,49.3114815,48.7999306,47.7201881,46.3433914,

    46.5303612,47.6294632,48.6012459,47.8567657,48.0604057,47.1352806,

    49.5724792,50.5566483,49.4182968,50.5578079,50.6883736,50.6333389,

    51.9766159,51.0595245,49.3751640,46.9667702,47.1658173,47.4411278,

    47.5360374,48.9914742,50.4747620,50.2728043,51.9117165,53.7627792};

 

  imsls_f_ts_outlier_identification(n_obs, model, series,

        IMSLS_NUM_OUTLIERS, &num_outliers,

        IMSLS_OUTLIER_STATISTICS_USER, outlier_stat,

        IMSLS_OMEGA_WEIGHTS_USER, omega,

        IMSLS_ARMA_PARAM_USER, parameters,

        IMSLS_RETURN_USER, result,

        IMSLS_RESIDUAL_SIGMA, &res_sigma,

        IMSLS_AIC, &aic,

        IMSLS_RELATIVE_ERROR, 1.0e-05,

        0);

 

  printf("\nARMA parameters:\n");

  for (i=0; i<=model[0]+model[1]; i++)

      printf("%d\t\t%lf\n", i, parameters[i]);

  printf("\nNumber of outliers: %d\n\n", num_outliers);

  printf("Outlier statistics:\n");

  printf("Time point\tOutlier type\n");

  for (i=0; i<num_outliers; i++)

      printf("%d\t\t%d\n", outlier_stat[2*i], outlier_stat[2*i+1]);

  printf("\nOmega statistics:\n");

  printf("Time point\tomega\n");

  for (i=0; i<num_outliers; i++)

      printf("%d%21.6f\n", outlier_stat[2*i], omega[i]);

  printf("\nRSE: %lf\n", res_sigma);

  printf("AIC: %lf\n\n", aic);

}

 

 Output

 

ARMA parameters:

0               10.833087

1               0.785139

2               -0.496548

 

Number of outliers: 2

 

Outlier statistics:

Time point      Outlier type

150             1

200             3

 

Omega statistics:

Time point      omega

150             4.477888

200             3.381441

 

RSE: 1.007223

AIC: 1417.044434

RW_logo.jpg
Contact Support