CSCON
Computes a cubic spline interpolant that is consistent with the concavity of the data.
Required Arguments
XDATA — Array of length NDATA containing the data point abscissas. (Input)
The data point abscissas must be distinct.
The data point abscissas must be distinct.
FDATA — Array of length NDATA containing the data point ordinates. (Input)
IBREAK — The number of breakpoints. (Output)
It will be less than 2 * NDATA.
It will be less than 2 * NDATA.
BREAK — Array of length IBREAK containing the breakpoints for the piecewise cubic representation in its first IBREAK positions. (Output)
The dimension of BREAK must be at least 2 * NDATA.
The dimension of BREAK must be at least 2 * NDATA.
CSCOEF — Matrix of size 4 by N where N is the dimension of BREAK. (Output)
The first IBREAK − 1 columns of CSCOEF contain the local coefficients of the cubic pieces.
The first IBREAK − 1 columns of CSCOEF contain the local coefficients of the cubic pieces.
Optional Arguments
NDATA — Number of data points. (Input)
NDATA must be at least 3.
Default: NDATA = size (XDATA,1).
NDATA must be at least 3.
Default: NDATA = size (XDATA,1).
FORTRAN 90 Interface
Generic: CALL CSCON (XDATA, FDATA, IBREAK, BREAK, CSCOEF [, …])
Specific: The specific interface names are S_CSCON and D_CSCON.
FORTRAN 77 Interface
Single: CALL CSCON (NDATA, XDATA, FDATA, IBREAK, BREAK, CSCOEF)
Double: The double precision name is DCSCON.
Description
The routine CSCON computes a cubic spline interpolant to n = NDATA data points {xi, fi} for i = 1, …, n. For ease of explanation, we will assume that xi < xi+1, although it is not necessary for the user to sort these data values. If the data are strictly convex, then the computed spline is convex, C2, and minimizes the expression
over all convex C 1 functions that interpolate the data. In the general case when the data have both convex and concave regions, the convexity of the spline is consistent with the data and the above integral is minimized under the appropriate constraints. For more information on this interpolation scheme, we refer the reader to Micchelli et al. (1985) and Irvine et al. (1986).
One important feature of the splines produced by this subroutine is that it is not possible, a priori, to predict the number of breakpoints of the resulting interpolant. In most cases, there will be breakpoints at places other than data locations. The method is nonlinear; and although the interpolant is a piecewise cubic, cubic polynomials are not reproduced. (However, linear polynomials are reproduced.) This routine should be used when it is important to preserve the convex and concave regions implied by the data.
Comments
1. Workspace may be explicitly provided, if desired, by use of C2CON/DC2CON. The reference is:
CALL C2CON (NDATA, XDATA, FDATA, IBREAK, BREAK, CSCOEF, ITMAX, XSRT, FSRT, A, Y, DIVD, ID, WK)
The additional arguments are as follows:
ITMAX — Maximum number of iterations of Newton’s method. (Input)
XSRT — Work array of length NDATA to hold the sorted XDATA values.
FSRT — Work array of length NDATA to hold the sorted FDATA values.
A — Work array of length NDATA.
Y — Work array of length NDATA − 2.
DIVD — Work array of length NDATA − 2.
ID — Integer work array of length NDATA.
WK — Work array of length 5 * (NDATA − 2).
2. Informational errors
Type | Code | Description |
|---|---|---|
3 | 16 | Maximum number of iterations exceeded, call C2CON/DC2CON to set a larger number for ITMAX. |
4 | 3 | The XDATA values must be distinct. |
4. The default value for ITMAX is 25. This can be reset by calling C2CON/DC2CON directly.
Example
We first compute the shape-preserving interpolant using CSCON, and display the coefficients and breakpoints. Second, we interpolate the same data using CSINT in a program not shown and overlay the two results. The graph of the result from CSINT is represented by the dashed line. Notice the extra inflection points in the curve produced by CSINT.
USE CSCON_INT
USE UMACH_INT
USE WRRRL_INT
IMPLICIT NONE
! Specifications
INTEGER NDATA
PARAMETER (NDATA=9)
!
INTEGER IBREAK, NOUT
REAL BREAK(2*NDATA), CSCOEF(4,2*NDATA), FDATA(NDATA),&
XDATA(NDATA)
CHARACTER CLABEL(14)*2, RLABEL(4)*2
!
DATA XDATA/0.0, .1, .2, .3, .4, .5, .6, .8, 1./
DATA FDATA/0.0, .9, .95, .9, .1, .05, .05, .2, 1./
DATA RLABEL/' 1', ' 2', ' 3', ' 4'/
DATA CLABEL/' ', ' 1', ' 2', ' 3', ' 4', ' 5', ' 6',&
' 7', ' 8', ' 9', '10', '11', '12', '13'/
! Compute cubic spline interpolant
CALL CSCON (XDATA, FDATA, IBREAK, BREAK, CSCOEF)
! Get output unit number
CALL UMACH (2, NOUT)
! Print the BREAK points and the
! coefficients (CSCOEF) for
! checking purposes.
WRITE (NOUT,'(1X,A,I2)') 'IBREAK = ', IBREAK
CALL WRRRL ('BREAK', BREAK, RLABEL, CLABEL, 1, IBREAK, 1, &
FMT='(F9.3)')
CALL WRRRL ('CSCOEF', CSCOEF, RLABEL, CLABEL, 4, IBREAK, 4, &
FMT='(F9.3)')
END
Output
IBREAK = 13
BREAK
1 2 3 4 5 6
1 0.000 0.100 0.136 0.200 0.259 0.300
7 8 9 10 11 12
1 0.400 0.436 0.500 0.600 0.609 0.800
13
1 1.000
CSCOEF
1 2 3 4 5 6
1 0.000 0.900 0.942 0.950 0.958 0.900
2 11.886 3.228 0.131 0.131 0.131 -4.434
3 0.000 -173.170 0.000 0.000 0.000 220.218
4 -1731.699 4841.604 0.000 0.000 -5312.082 4466.875
7 8 9 10 11 12
1 0.100 0.050 0.050 0.050 0.050 0.200
2 -4.121 0.000 0.000 0.000 0.000 2.356
3 226.470 0.000 0.000 0.000 0.000 24.664
4 -6222.348 0.000 0.000 0.000 129.115 123.321
13
1 1.000
2 0.000
3 0.000
4 0.000
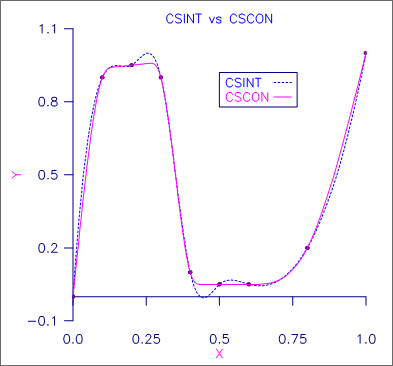
Figure 6, CSCON vs. CSINT