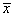The basic linear algebra subprograms, normally referred to as the BLAS, are routines for low-level operations such as dot products, matrix times vector, and matrix times matrix. Lawson et al. (1979) published the original set of 38 BLAS. The IMSL BLAS collection includes these 38 subprograms plus additional ones that extend their functionality. Since Dongarra et al. (1988 and 1990) published extensions to this set, it is customary to refer to the original 38 as Level 1 BLAS. The Level 1 operations are performed on one or two vectors of data. An extended set of subprograms perform operations involving a matrix and one or two vectors. These are called the Level 2 BLAS (see Specification of the Level 2 BLAS). An additional extended set of operations on matrices is called the Level 3 BLAS (see Specification of the Level 3 BLAS).
Users of the BLAS will often benefit from using versions of the BLAS supplied by hardware vendors, if available. This can provide for more efficient execution of many application programs. The BLAS provided by IMSL are written in FORTRAN. Those supplied by vendors may be written in other languages, such as assembler. The documentation given below for the BLAS is compatible with a vendor's version of the BLAS that conforms to the published specifications.
Programming Notes for Level 1 BLAS
The Level 1 BLAS do not follow the usual IMSL naming conventions. Instead, the names consist of a prefix of one or more of the letters “I,” “S,” “D,” “C” and “Z;” a root name; and sometimes a suffix. For subprograms involving a mixture of data types, the output type is indicated by the first prefix letter. The suffix denotes a variant algorithm. The prefix denotes the type of the operation according to the following table:
|
I Integer |
|
|
S Real |
C Complex |
|
D Double |
Z Double complex |
|
SD Single and Double |
CZ Single and double complex |
|
DQ Double and Quadruple |
ZQ Double and quadruple complex |
Vector arguments have an increment parameter that specifies the storage space or stride between elements. The correspondence between the vectors x and y and the arguments SX and SY, and INCX and INCY is

Function subprograms SXYZ and DXYZ refer to a third vector argument z. The storage increment INCZ for z is defined like INCX, INCY. In the Level 1 BLAS, only positive values of INCX are allowed for operations that have a single vector argument. The loops in all of the Level 1 BLAS process the vector arguments in order of increasing i. For INCX, INCY, INCZ < 0, this implies processing in reverse storage order.
The function subprograms in the Level 1 BLAS are all illustrated by means of an assignment statement. For example, see SDOT. Any value of a function subprogram can be used in an expression or as a parameter passed to a subprogram as long as the data types agree.
Descriptions of the Level 1 BLAS Subprograms
The set of Level 1 BLAS are summarized in Table 9.1. This table also lists the page numbers where the subprograms are described in more detail.
Specification of the Level 1 BLAS
With the definitions,
MX = max {1, 1 + (N - 1)|INCX|}
MY = max {1, 1 + (N - 1)|INCY|}
MZ = max {1, 1 + (N - 1)|INCZ|}
the subprogram descriptions assume the following FORTRAN declarations:
IMPLICIT INTEGER
(I-N)
IMPLICIT
REAL
S
IMPLICIT DOUBLE PRECISION D
IMPLICIT
COMPLEX C
IMPLICIT
DOUBLE COMPLEX
Z
INTEGER
IX(MX)
REAL
SX(MX), SY(MY),
SZ(MZ),
SPARAM(5)
DOUBLE
PRECISION DX(MX), DY(MY),
DZ(MZ),
DPARAM(5)
DOUBLE
PRECISION DACC(2),
DZACC(4)
COMPLEX
CX(MX), CY(MY)
DOUBLE
COMPLEX
ZX(MX), ZY(MY)
Since FORTRAN 77 does not include the type DOUBLE COMPLEX, subprograms with DOUBLE COMPLEX arguments are not available for all systems. Some systems use the declaration COMPLEX * 16 instead of DOUBLE COMPLEX.
In the following descriptions, the original BLAS are marked with an * in the left column.
Table 9.1: Level 1 Basic Linear Algebra Subprograms
|
|
| |||||||||||||
|
|
| |||||||||||||
|
|
| |||||||||||||
|
|
| |||||||||||||
|
|
| |||||||||||||
†Higher precision accumulation used
Set a Vector to a Constant Value
CALL ISET
(N, IA, IX, INCX)
CALL
SSET (N,
SA,
SX,
INCX)
CALL DSET (N, DA, DX, INCX)
CALL
CSET (N,
CA,
CX,
INCX)
CALL ZSET (N, ZA, ZX, INCX)
These subprograms set xi ← a for i = 1, 2, …, N. If N ≤ 0, then the subprograms return immediately.
Copy a Vector
CALL ICOPY (N, IX, INCX, IY, INCY)
*CALL SCOPY
(N, SX, INCX, SY, INCY)
*CALL DCOPY
(N, DX, INCX, DY, INCY)
*CALL CCOPY
(N, CX, INCX, CY,
INCY)
CALL ZCOPY (N, ZX, INCX, ZY, INCY)
These subprograms set yi ← xi for i = 1, 2, …, N. If N ≤ 0, then the subprograms return immediately.
Scale a Vector
*CALL SSCAL
(N, SA, SX, INCX)
*CALL DSCAL
(N, DA, DX, INCX)
*CALL CSCAL
(N, CA, CX,
INCX)
CALL ZSCAL (N, ZA, ZX, INCX)
*CALL CSSCAL
(N, SA, CX,
INCX)
CALL ZDSCAL (N, DA, ZX, INCX)
These subprograms set xi ← axi for i = 1, 2, …, N. If N ≤ 0, then the subprograms return immediately. CAUTION: For CSSCAL and ZDSCAL, the scalar quantity a is real and the vector x is complex.
Multiply a Vector by a Constant
CALL SVCAL (N, SA, SX, INCX, SY, INCY)
CALL
DVCAL (N,
DA,
DX,
INCX,
DY,
INCY)
CALL CVCAL (N, CA, CX, INCX, CY, INCY)
CALL
ZVCAL (N,
ZA,
ZX,
INCX,
ZY,
INCY)
CALL CSVCAL (N, SA, CX, INCX, CY, INCY)
CALL
ZDVCAL (N,
DA,
ZX,
INCX,
ZY,
INCY)
These subprograms set yi ← axi for i = 1, 2, …, N. If N ≤ 0, then the subprograms return immediately. CAUTION: For CSVCAL and ZDVCAL, the scalar quantity a is real and the vector x is complex.
Add a Constant to a Vector
CALL IADD (N, IA, IX, INCX)
CALL
SADD (N,
SA,
SX,
INCX)
CALL DADD (N, DA, DX, INCX)
CALL
CADD (N,
CA,
CX,
INCX)
CALL ZADD (N, ZA, ZX, INCX)
These subprograms set xi ← xi + a for i = 1, 2, …, N. If N ≤ 0, then the subprograms return immediately.
Subtract a Vector from a Constant
CALL ISUB (N, IA, IX, INCX)
CALL
SSUB (N,
SA,
SX,
INCX)
CALL DSUB (N, DA, DX, INCX)
CALL
CSUB (N,
CA,
CX,
INCX)
CALL ZSUB (N, ZA, ZX, INCX)
These subprograms set xi ← a - xi for i = 1, 2, …, N. If N ≤ 0, then the subprograms return immediately.
Constant Times a Vector Plus a Vector
*CALL SAXPY
(N, SA, SX, INCX, SY, INCY)
*CALL DAXPY
(N, DA, DX, INCX, DY, INCY)
*CALL CAXPY
(N, CA, CX, INCX, CY,
INCY)
CALL ZAXPY (N, ZA, ZX, INCX, ZY, INCY)
These subprograms set yi ← axi + yi for i = 1, 2, …, N. If N ≤ 0, then the subprograms return immediately.
Swap Two Vectors
CALL ISWAP (N, IX, INCX, IY, INCY)
*CALL SSWAP
(N, SX, INCX, SY, INCY)
*CALL DSWAP
(N, DX, INCX, DY, INCY)
*CALL CSWAP
(N, CX, INCX, CY,
INCY)
CALL ZSWAP (N, ZX, INCX, ZY, INCY)
These subprograms perform the exchange yi ↔ xi for i = 1, 2, …, N. If N ≤ 0, then the subprograms return immediately.
Dot Product
*SW =
SDOT (N,
SX,
INCX,
SY,
INCY)
*DW =
DDOT (N,
DX,
INCX,
DY,
INCY)
*CW = CDOTU
(N, CX, INCX, CY, INCY)
*CW = CDOTC
(N, CX, INCX, CY,
INCY)
ZW = ZDOTU (N, ZX, INCX, ZY,
INCY)
ZW = ZDOTC (N, ZX, INCX, ZY, INCY)
The function subprograms SDOT, DDOT, CDOTU, and ZDOTU compute
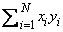
The function subprograms CDOTC and ZDOTC compute

The suffix C indicates that the complex conjugates of xi are used. The suffix U indicates that the unconjugated values of xi are used. If N ≤ 0, then the subprograms return zero.
Dot Product with Higher Precision Accumulation
*DW =
DSDOT (N,
SX,
INCX,
SY,
INCY)
CW = CZDOTC (N, CX, INCX, CY,
INCY)
CW = CZDOTU (N, CX, INCX, CY,
INCY)
ZW = ZQDOTC (N, ZX, INCX, ZY,
INCY)
ZW = ZQDOTU (N, ZX, INCX, ZY, INCY)
The function subprogram DSDOT computes
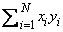
using double precision accumulation. The function subprograms CZDOTU and ZQDOTU compute
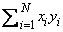
using double and quadruple complex accumulation, respectively. The function subprograms CZDOTC and ZQDOTC compute

using double and quadruple complex accumulation, respectively. If N ≤ 0, then the subprograms return zero.
Constant Plus Dot Product with Higher Precision Accumulation
*SW = SDSDOT
(N, SA, SX, INCX, SY,
INCY)
DW = DQDDOT (N, DA, DX, INCX, DY,
INCY)
CW = CZCDOT (N, CA, CX, INCX, CY,
INCY)
CW = CZUDOT (N, CA, CX, INCX, CY,
INCY)
ZW = ZQCDOT (N, ZA, ZX, INCX, ZY,
INCY)
ZW = ZQUDOT (N, ZA, ZX, INCX, ZY, INCY)
The function subprograms SDSDOT, DQDDOT, CZUDOT, and ZQUDOT compute

using higher precision accumulation where SDSDOT uses double precision accumulation, DQDDOT uses quadruple precision accumulation, CZUDOT uses double complex accumulation, and ZQUDOT uses quadruple complex accumulation. The function subprograms CZCDOT and ZQCDOT compute
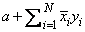
using double complex and quadruple complex accumulation, respectively. If N ≤ 0, then the subprograms return zero.
Dot Product Using the Accumulator
SW = SDDOTI
(N, SB, DACC, SX, INCX, SY,
INCY)
SW = SDDOTA (N, SB, DACC, SX, INCX, SY,
INCY)
CW = CZDOTI (N, CB, DACC, CX, INCX, CY,
INCY)
CW = CZDOTA (N, CB, DACC, CX, INCX, CY, INCY)
*DW =
DQDOTI (N,
DB,
DACC,
DX,
INCX,
DY,
INCY)
*DW =
DQDOTA (N,
DB,
DACC,
DX,
INCX,
DY,
INCY)
ZW = ZQDOTI (N, ZB, DZACC, ZX, INCX, ZY,
INCY)
ZW = ZQDOTA (N, ZB, DZACC, ZX, INCX, ZY, INCY)
The variable DACC, a double precision array of length two, is used as a quadruple precision accumulator. DZACC, a double precision array of length four, is its complex analog. The function subprograms, with a name ending in I, initialize DACC to zero. All of the function subprograms then compute
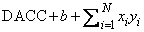
and store the result in DACC. The result, converted to the precision of the function, is also returned as the function value. If N ≤ 0, then the function subprograms return zero.
Hadamard Product
CALL SHPROD (N, SX, INCX, SY, INCY, SZ, INCZ)
CALL
DHPROD (N,
DX,
INCX,
DY,
INCY,
DZ,
INCZ)
These subprograms set zi ← xiyi for i = 1, 2, …, N. If N ≤ 0, then the subprograms return immediately.
Triple Inner Product
SW = SXYZ (N, SX, INCX, SY, INCY, SZ, INCZ)
DW =
DXYZ (N,
DX,
INCX,
DY,
INCY,
DZ,
INCZ)
These function subprograms compute
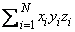
If N ≤ 0 then the subprograms return zero.
Sum of the Elements of a Vector
IW = ISUM (N, IX, INCX)
SW =
SSUM (N,
SX,
INCX)
DW = DSUM (N, DX, INCX)
These function subprograms compute
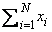
If N ≤ 0, then the subprograms return zero.
Sum of the Absolute Values of the Elements of a Vector
*SW = SASUM
(N, SX, INCX)
*DW = DASUM
(N, DX, INCX)
*SW = SCASUM
(N, CX,
INCX)
DW = DZASUM (N, ZX, INCX)
The function subprograms SASUM and DASUM compute
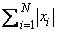
The function subprograms SCASUM and DZASUM compute
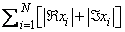
If N ≤ 0, then the subprograms return zero. CAUTION: For SCASUM and DZASUM, the function subprogram returns a real value.
Euclidean or 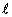 2 Norm of a
Vector
2 Norm of a
Vector
*SW = SNRM2
(N, SX, INCX)
*DW = DNRM2
(N, DX, INCX)
*SW = SCNRM2
(N, CX,
INCX)
DW = DZNRM2 (N, ZX, INCX)
These function subprograms compute
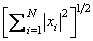
If N ≤ 0, then the subprograms return zero. CAUTION: For SCNRM2 and DZNRM2, the function subprogram returns a real value.
Product of the Elements of a Vector
SW = SPRDCT (N, SX, INCX)
DW =
DPRDCT (N,
DX,
INCX)
These function subprograms compute

If N ≤ 0, then the subprograms return zero.
Index of Element Having Minimum Value
IW = IIMIN (N, IX, INCX)
IW =
ISMIN (N,
SX,
INCX)
IW = IDMIN (N, DX, INCX)
These function subprograms compute the smallest index i such that xi = min1≤j≤N xj. If N ≤ 0, then the subprograms return zero.
Index of Element Having Maximum Value
IW = IIMAX (N, IX, INCX)
IW =
ISMAX (N,
SX,
INCX)
IW = IDMAX (N, DX, INCX)
These function subprograms compute the smallest index i such thatxi = max1≤j≤N xj. If N ≤ 0, then the subprograms return zero.
Index of Element Having Minimum Absolute Value
IW = ISAMIN (N, SX, INCX)
IW =
IDAMIN (N,
DX,
INCX)
IW = ICAMIN (N, CX, INCX)
IW =
IZAMIN (N,
ZX,
INCX)
The function subprograms ISAMIN
and IDAMIN
compute the smallest index i such that
|xi| = min1≤j≤N |xj|. The function
subprograms ICAMIN
and IZAMIN
compute the smallest index i such that
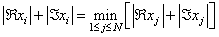
If N ≤ 0, then the subprograms return zero.
Index of Element Having Maximum Absolute Value
*IW = ISAMAX
(N, SX, INCX)
*IW = IDAMAX
(N, DX, INCX)
*IW = ICAMAX
(N, CX,
INCX)
IW = IZAMAX (N, ZX, INCX)
The function subprograms ISAMAX
and IDAMAX
compute the smallest index i such that
|xi| = max1≤j≤N |xj|. The function
subprograms ICAMAX
and IZAMAX
compute the smallest index i such that
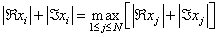
If N ≤ 0, then the subprograms return zero.
Construct a Givens Plane Rotation
*CALL SROTG
(SA,
SB,
SC,
SS)
*CALL DROTG
(SA,
SB,
SC,
SS)
Given the values a and b, these subprograms compute
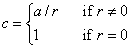
and
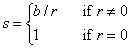
where r = σ(a2 + b2) 1/2 and
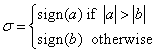
Then, the values c, s and r satisfy the matrix equation
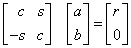
The introduction of σ is not essential to the computation of the Givens rotation matrix; but its use permits later stable reconstruction of c and s from just one stored number, an idea due to Stewart (1976). For this purpose, the subprogram also computes
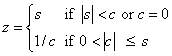
In addition to returning c and s, the subprograms return r overwriting a, and z overwriting b.
Reconstruction of c and s from z can be done as follows:
If z = 1, then set c = 0 and s = 1
If |z| < 1, then set
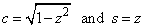
If |z| > 1, then set
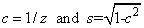
Apply a Plane Rotation
*CALL SROT
(N, SX, INCX, SY, INCY, SC, SS)
*CALL DROT
(N, DX, INCX, DY, INCY, DC,
DS)
CALL CSROT (N, CX, INCX, CY, INCY, SC,
SS)
CALL ZDROT (N, ZX, INCX, ZY, INCY, DC, DS)
These subprograms compute
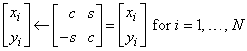
If N ≤ 0, then the subprograms return immediately. CAUTION: For CSROT and ZDROT, the scalar quantities c and s are real, and x and y are complex.
Construct a Modified Givens Transformation
*CALL SROTMG
(SD1,
SD2,
SX1,
SY1,
SPARAM)
*CALL DROTMG
(DD1,
DD2,
DX1,
DY1,
DPARAM)
The input quantities d1, d2, x1 and y1 define a 2-vector [w1, z1]T by the following:
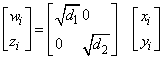
The subprograms determine the modified Givens rotation matrix H that transforms y1, and thus, z1 to zero. They also replace d1, d2 and x1 with
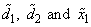
respectively. That is,
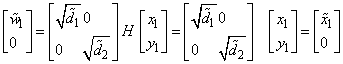
A representation of this matrix is stored in the array SPARAM or DPARAM. The form of the matrix H is flagged by PARAM(1).
PARAM(1) = 1. In this case,
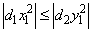
and
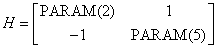
The elements PARAM(3) and PARAM(4) are not changed.
PARAM(1) = 0. In this case,
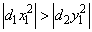
and
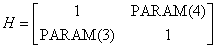
The elements PARAM(2) and PARAM(5) are not changed.
PARAM(1) = -1. In this case, rescaling was done and
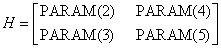
PARAM(1) = -2. In this case, H = I where I is the identity matrix. The elements PARAM(2), PARAM(3), PARAM(4) and PARAM(5) are not changed.
The values of d1, d2 and x1are changed to represent the effect of the transformation. The quantity y1, which would be zeroed by the transformation, is left unchanged.
The input value of d1 should be nonnegative, but d2 can be negative for the purpose of removing data from a least-squares problem.
See Lawson et al. (1979) for further details.
Apply a Modified Givens Transformation
*CALL SROTM
(N, SX, INCX, SY, INCY,
SPARAM)
*CALL DROTM
(N, DX, INCX, DY, INCY,
DPARAM)
CALL CSROTM (N, CX, INCX, CY, INCY,
SPARAM)
CALL ZDROTM (N, ZX, INCX, ZY, INCY, DPARAM)
If PARAM(1) = 1.0, then these subprograms compute
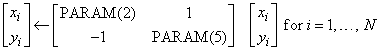
If PARAM(1) = 0.0, then the subprograms compute

If PARAM(1) = -1.0, then the subprograms compute

If N ≤ 0 or if PARAM(1) = -2.0, then the subprograms return immediately. CAUTION: For CSROTM and ZDROTM, the scalar quantities PARAM(*) are real and x and y are complex.
Programming Notes for Level 2 and Level 3 BLAS
For definitions of the matrix data structures used in the discussion below, see Reference Material. The Level 2 and Level 3 BLAS, like the Level 1 BLAS, do not follow the IMSL naming conventions. Instead, the names consist of a prefix of one of the letters “S,” “D,” “C” or “Z.” Next is a root name denoting the kind of matrix. This is followed by a suffix indicating the type of the operation.1 The prefix denotes the type of operation according to the following table:
|
S Real |
C Complex |
|
D Double |
Z Double Complex |
The root names for the kind of matrix:
|
GE General |
GB General Band |
|
SY Symmetric |
SB Symmetric Band |
|
HE Hermitian |
HB Hermitian Band |
|
TR Triangular |
TB Triangular Band |
The suffixes for the type of operation:
|
MV |
Matrix-Vector Product |
SV |
Solve for Vector |
|
R |
Rank-One Update |
|
|
|
RU |
Rank-One Update, |
RC |
Rank-One Update, |
|
R2 |
Rank-Two Update |
|
|
|
MM |
Matrix-Multiply |
SM |
Symmetric Matrix Multiply |
|
RK |
Rank-K Update |
R2K |
Rank 2K Update |
1IMSL does not support the Packed Symmetric, Packed-Hermitian, or Packed-Triangular data structures, with respective root names SP, HP or TP, nor any extended precision versions of the Level 2 BLAS.
The specifications of the operations are provided by subprogram arguments of CHARACTER*1 data type. Both lower and upper case of the letter have the same meaning:
|
TRANS, TRANSA, TRANSB |
'N' |
No Transpose |
|
|
'T' |
Transpose |
|
|
'C' |
Conjugage and Transpose |
|
UPLO |
'L' |
Lower Triangular |
|
|
'U' |
Upper Triangular |
|
DIAGNL |
'N' |
Non-unit Triangular |
|
|
'U' |
Unit Triangular |
|
SIDE |
'L' |
Multiply “A” Matrix on Left side or |
|
|
'R' |
Right side of the “B” matrix |
Note: See the “Triangular Mode” section in the Reference Material for definitions of these terms.
Descriptions of the Level 2 and Level 3 BLAS
The subprograms for Level 2 and Level 3 BLAS that perform
operations involving the expression βy or βC do not require that
the contents of y or C be defined when β = 0. In that case, the
expression βy or
βC is defined to
be zero. Note that for the _GEMV
and _GBMV
subprograms, the dimensions of the vectors x and y are implied by
the specification of the operation. If
TRANS
= 'N',
the dimension of y is m; if TRANS
= 'T'
or = 'C',
the dimension of y is n. The Level 2 and Level 3 BLAS are
summarized in Table 9.2. This table also lists the page numbers where the
subprograms are described in more detail.
Specification of the Level 2 BLAS
Type and dimension for variables occurring in the subprogram specifications are
INTEGER
INCX, INCY, NCODA, NLCA, NUCA, LDA, M,
N
CHARACTER*1 DIAGNL, TRANS,
UPLO
REAL
SALPHA, SBETA, SX(*), SY(*), SA(LDA,*)
DOUBLE PRECISION DALPHA, DBETA,
DX(*), DY(*),
DA(LDA,*)
COMPLEX
CALPHA, CBETA, CX(*), CY(*), CA(LDA,*)
DOUBLE COMPLEX
ZALPHA, ZBETA, ZX(*), ZY(*), ZA(LDA,*)
There is a lower bound on the leading dimension LDA. It must be ≥ the number of rows in the matrix that is contained in this array. Vector arguments have an increment parameter that specifies the storage space or stride between elements. The correspondence between the vector x, y and the arguments SX, SY and INCX, INCY is

In the Level 2 BLAS, only nonzero values of INCX, INCY are allowed for operations that have vector arguments. The Level 3 BLAS do not refer to INCX, INCY.
Specification of the Level 3 BLAS
Type and dimension for variables occurring in the subprogram specifications are
INTEGER
K, LDA, LDB, LDC, M, N
CHARACTER*1
DIAGNL, TRANS, TRANSA, TRANSB, SIDE,
UPLO
REAL
SALPHA, SBETA, SA(LDA,*), SB(LDB,*),
SC(LDC,*)
DOUBLE
PRECISION DALPHA, DBETA, DA(LDA,*), DB(LDB,*),
DC(LDC,*)
COMPLEX
CALPHA, CBETA, CA(LDA,*), CB(LDB,*),
CC(LDC,*)
DOUBLE COMPLEX ZALPHA, ZBETA, ZA(LDA,*),
ZB(LDB,*),
ZC(LDC,*)
Each of the integers K, M, N must be ≥ 0. It is an error if any of them are < 0. If any of them are = 0, the subprograms return immediately. There are lower bounds on the leading dimensions LDA, LDB, LDC. Each must be ≥ the number of rows in the matrix that is contained in this array.
Table 9.2: Level 2 and 3 Basic Linear Algebra Subprograms
|
Rank-One Matrix Update, |
||||||
Matrix–Vector Multiply, General
CALL SGEMV
(TRANS,
M,
N,
SALPHA,
SA,
LDA,
SX,
INCX,
SBETA,
SY,
INCY)
CALL DGEMV (TRANS, M, N, DALPHA, DA, LDA, DX, INCX, DBETA, DY, INCY)
CALL
CGEMV (TRANS,
M,
N,
CALPHA,
CA,
LDA,
CX,
INCX,
CBETA,
CY,
INCY)
CALL ZGEMV (TRANS, M, N, ZALPHA, ZA, LDA, ZX, INCX, ZBETA, ZY, INCY)
For all data types, A is an M ´ N matrix. These subprograms set
y to one of the expressions:
y ← αAx + βy, y ← αATx + βy, or for complex
data,
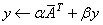
The character flag TRANS determines the operation.
Matrix–Vector Multiply, Banded
CALL SGBMV (TRANS, M, N, NLCA, NUCA SALPHA, SA, LDA, SX, INCX, SBETA, SY, INCY)
CALL DGBMV (TRANS, M, N, NLCA, NUCA DALPHA, DA, LDA, DX, INCX, DBETA, DY, INCY)
CALL CGBMV (TRANS, M, N, NLCA, NUCA CALPHA, CA, LDA, CX, INCX, BETA, CY, INCY)
CALL ZGBMV (TRANS, M, N, NLCA, NUCA ZALPHA, ZA, LDA, ZX, INCX, ZBETA, ZY, INCY)
For all data types, A is an M ´ N matrix with NLCA lower codiagonals and NUCA upper codiagonals. The matrix is stored in band storage mode. These subprograms set y to one of the expressions: y ← αAx + βy, y ← αATx + βy, or for complex data,
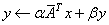
The character flag TRANS determines the operation.
Matrix-Vector Multiply, Hermitian
CALL CHEMV (UPLO, N, CALPHA, CA, LDA, CX, INCX, CBETA, CY, INCY)
CALL
ZHEMV (UPLO,
N,
ZALPHA,
ZA,
LDA,
ZX,
INCX,
ZBETA,
ZY,
INCY)
For all data types, A is an N ´ N matrix. These subprograms set y ← αAx + βy where A is an Hermitian matrix. The matrix A is either referenced using its upper or lower triangular part. The character flag UPLO determines the part used.
Matrix-Vector Multiply, Hermitian and Banded
CALL CHBMV (UPLO, N, NCODA, CALPHA, CA, LDA, CX, INCX, CBETA, CY, INCY)
CALL
ZHBMV (UPLO,
N,
NCODA,
ZALPHA,
ZA,
LDA,
ZX,
INCX,
ZBETA,
ZY,
INCY)
For all data types, A is an N ´ N matrix with NCODA codiagonals. The matrix is stored in band Hermitian storage mode. These subprograms set y ← αAx + βy. The matrix A is either referenced using its upper or lower triangular part. The character flag UPLO determines the part used.
Matrix-Vector Multiply, Symmetric and Real
CALL SSYMV (UPLO, N, SALPHA, SA, LDA, SX, INCX, SBETA, SY, INCY)
CALL
DSYMV (UPLO,
N,
DALPHA,
DA,
LDA,
DX,
INCX,
DBETA,
DY,
INCY)
For all data types, A is an N ´ N matrix. These subprograms set y ← αAx + βy where A is a symmetric matrix. The matrix A is either referenced using its upper or lower triangular part. The character flag UPLO determines the part used.
Matrix-Vector Multiply, Symmetric and Banded
CALL SSBMV (UPLO, N, NCODA, SALPHA, SA, LDA, SX, INCX, SBETA, SY, INCY)
CALL
DSBMV (UPLO,
N,
NCODA,
DALPHA,
DA,
LDA,
DX,
INCX,
DBETA,
DY,
INCY)
For all data types, A is an N ´ N matrix with NCODA codiagonals. The matrix is stored in band symmetric storage mode. These subprograms set y ← αAx + βy. The matrix A is either referenced using its upper or lower triangular part. The character flag UPLO determines the part used.
Matrix-Vector Multiply, Triangular
CALL STRMV (UPLO, TRANS, DIAGNL, N, SA, LDA, SX, INCX)
CALL
DTRMV (UPLO,
TRANS,
DIAGNL,
N,
DA,
LDA,
DX,
INCX)
CALL CTRMV (UPLO, TRANS, DIAGNL, N, CA, LDA, CX, INCX)
CALL
ZTRMV (UPLO,
TRANS,
DIAGNL,
N,
ZA,
LDA,
ZX,
INCX)
For all data types, A is an N ´ N triangular matrix. These subprograms set x to one of the expressions: x ← Ax, x ←ATx, or for complex data,
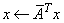
The matrix A is either referenced using its upper or lower triangular part and is unit or nonunit triangular. The character flags UPLO, TRANS, and DIAGNL determine the part of the matrix used and the operation performed.
Matrix-Vector Multiply, Triangular and Banded
CALL STBMV (UPLO, TRANS, DIAGNL, N, NCODA, SA, LDA, SX, INCX)
CALL
DTBMV (UPLO,
TRANS,
DIAGNL,
N,
NCODA,
DA,
LDA,
DX,
INCX)
CALL CTBMV (UPLO, TRANS, DIAGNL, N, NCODA, CA, LDA, CX, INCX)
CALL
ZTBMV (UPLO,
TRANS,
DIAGNL,
N,
NCODA,
ZA,
LDA,
ZX,
INCX)
For all data types, A is an N ´ N matrix with NCODA codiagonals. The matrix is stored in band triangular storage mode. These subprograms set x to one of the expressions: x ← Ax, x ← ATx, or for complex data,
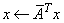
The matrix A is either referenced using its upper or lower triangular part and is unit or nonunit triangular. The character flags UPLO, TRANS, and DIAGNL determine the part of the matrix used and the operation performed.
Matrix-Vector Solve, Triangular
CALL STRSV (UPLO, TRANS, DIAGNL, N, SA, LDA, SX, INCX)
CALL
DTRSV (UPLO,
TRANS,
DIAGNL,
N,
DA,
LDA,
DX,
INCX)
CALL CTRSV (UPLO, TRANS, DIAGNL, N, CA, LDA, CX, INCX)
CALL
ZTRSV (UPLO,
TRANS,
DIAGNL,
N,
ZA,
LDA,
ZX,
INCX)
For all data types, A is an N ´ N triangular matrix. These subprograms solve x for one of the expressions: x ←← A-1x, x ← (A-1)Tx, or for complex data,
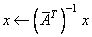
The matrix A is either referenced using its upper or lower triangular part and is unit or nonunit triangular. The character flags UPLO, TRANS, and DIAGNL determine the part of the matrix used and the operation performed.
Matrix-Vector Solve, Triangular and Banded
CALL STBSV (UPLO, TRANS, DIAGNL, N, NCODA, SA, LDA, SX, INCX)
CALL
DTBSV (UPLO,
TRANS,
DIAGNL,
N,
NCODA,
DA,
LDA,
DX,
INCX)
CALL CTBSV (UPLO, TRANS, DIAGNL, N, NCODA, CA, LDA, CX, INCX)
CALL
ZTBSV (UPLO,
TRANS,
DIAGNL,
N,
NCODA,
ZA,
LDA,
ZX,
INCX)
For all data types, A is an N ´ N triangular matrix with NCODA
codiagonals. The matrix is stored in band triangular storage mode. These
subprograms solve x for one of the expressions: x ← A-1x,
x
← (A-T) -1x, or for
complex data,
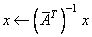
The matrix A is either referenced using its upper or lower triangular part and is unit or nonunit triangular. The character flags UPLO, TRANS, and DIAGNL determine the part of the matrix used and the operation performed.
Rank-One Matrix Update, General and Real
CALL SGER (M, N, SALPHA, SX, INCX, SY, INCY, SA, LDA)
CALL
DGER (M,
N,
DALPHA,
DX,
INCX,
DY,
INCY,
DA,
LDA)
For all data types, A is an M ´ N matrix. These subprograms set A ← A + αxyT.
Rank-One Matrix Update, General, Complex, and Transpose
CALL CGERU (M, N, CALPHA, CX, INCX, CY, INCY, CA, LDA)
CALL
ZGERU (M,
N,
ZALPHA,
ZX,
INCX,
ZY,
INCY,
ZA,
LDA)
For all data types, A is an M ´ N matrix. These subprograms set A ← A + αxyT.
Rank-One Matrix Update, General, Complex, and Conjugate Transpose
CALL CGERC (M, N, CALPHA, CX, INCX, CY, INCY, CA, LDA)
CALL
ZGERC (M,
N,
ZALPHA,
ZX,
INCX,
ZY,
INCY,
ZA,
LDA)
For all data types, A is an M ´ N matrix. These subprograms set
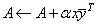
Rank-One Matrix Update, Hermitian and Conjugate Transpose
CALL CHER (UPLO, N, SALPHA, CX, INCX, CA, LDA)
CALL
ZHER (UPLO,
N,
DALPHA,
ZX,
INCX,
ZA,
LDA)
For all data types, A is an N ´ N matrix. These subprograms set
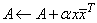
where A is Hermitian. The matrix A is either referenced by its upper or lower triangular part. The character flag UPLO determines the part used. CAUTION: Notice the scalar parameter α is real, and the data in the matrix and vector are complex.
Rank-Two Matrix Update, Hermitian and Conjugate Transpose
CALL CHER2 (UPLO, N, CALPHA, CX, INCX, CY, INCY, CA, LDA)
CALL
ZHER2 (UPLO,
N,
ZALPHA,
ZX,
INCX,
ZY,
INCY,
ZA,
LDA)
For all data types, A is an N ´ N matrix. These subprograms set
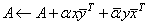
where A is an Hermitian matrix. The matrix A is either referenced by its upper or lower triangular part. The character flag UPLO determines the part used.
Rank-One Matrix Update, Symmetric and Real
CALL SSYR (UPLO, N, SALPHA, SX, INCX, SA, LDA)
CALL
DSYR (UPLO,
N,
DALPHA,
DX,
INCX,
DA,
LDA)
For all data types, A is an N ´ N matrix. These subprograms set A ← A + αxxT where A is a symmetric matrix. The matrix A is either referenced by its upper or lower triangular part. The character flag UPLO determines the part used.
Rank-Two Matrix Update, Symmetric and Real
CALL SSYR2 (UPLO, N, SALPHA, SX, INCX, SY, INCY, SA, LDA)
CALL
DSYR2 (UPLO,
N,
DALPHA,
DX,
INCX,
DY,
INCY,
DA,
LDA)
For all data types, A is an N ´ N matrix. These subprograms set A ← A + αxyT + αyxT where A is a symmetric matrix. The matrix A is referenced by its upper or lower triangular part. The character flag UPLO determines the part used.
Matrix-Matrix Multiply, General
CALL SGEMM (TRANSA, TRANSB, M, N, K, SALPHA, SA, LDA, SB, LDB, SBETA, SC, LDC)
CALL DGEMM (TRANSA, TRANSB, M, N, K, DALPHA, DA, LDA, DB, LDB, DBETA, DC, LDC)
CALL CGEMM (TRANSA, TRANSB, M, N, K, CALPHA, CA, LDA, CB, LDB, CBETA, CC, LDC)
CALL ZGEMM (TRANSA, TRANSB, M, N, K, ZALPHA, ZA, LDA, ZB, LDB, ZBETA, ZC, LDC)
For all data types, these subprograms set CM ×N to one of the expressions:
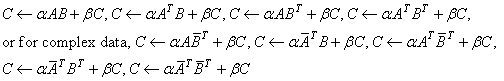
The character flags TRANSA and TRANSB determine the operation to be performed. Each matrix product has dimensions that follow from the fact that C has dimension M ´ N.
Matrix-Matrix Multiply, Symmetric
CALL SSYMM (SIDE, UPLO, M, N, SALPHA, SA, LDA, SB, LDB, SBETA, SC, LDC)
CALL
DSYMM (SIDE,
UPLO,
M,
N,
DALPHA,
DA,
LDA,
DB,
LDB,
DBETA,
DC,
LDC)
CALL CSYMM (SIDE, UPLO, M, N, CALPHA, CA, LDA, CB, LDB, CBETA, CC, LDC)
CALL
ZSYMM (SIDE,
UPLO,
M,
N,
ZALPHA,
ZA,
LDA,
ZB,
LDB,
ZBETA,
ZC,
LDC)
For all data types, these subprograms set CM×N to one of the
expressions: C ← αAB + βC or
C ←
αBA + βC, where A is a
symmetric matrix. The matrix A is referenced either by its upper or lower
triangular part. The character flags SIDE
and UPLO
determine the part of the matrix used and the operation performed.
Matrix-Matrix Multiply, Hermitian
CALL CHEMM (SIDE, UPLO, M, N, CALPHA, CA, LDA, CB, LDB, CBETA, CC, LDC)
CALL
ZHEMM (SIDE,
UPLO,
M,
N,
ZALPHA,
ZA,
LDA,
ZB,
LDB,
ZBETA,
ZC,
LDC)
For all data types, these subprograms set CM×N to one of the
expressions: C ← αAB + βC or
C ←
αBA + βC, where A is
an Hermitian matrix. The matrix A is referenced either by its upper or
lower triangular part. The character flags SIDE
and UPLO
determine the part of the matrix used and the operation performed.
Rank-k Update, Symmetric
CALL SSYRK
(UPLO,
TRANS,
N,
K,
SALPHA,
SA,
LDA,
SBETA,
SC,
LDC)
CALL DSYRK (UPLO, TRANS, N, K, DALPHA, DA, LDA, DBETA, DC, LDC)
CALL
CSYRK (UPLO,
TRANS,
N,
K,
CALPHA,
CA,
LDA,
CBETA,
CC,
LDC)
CALL ZSYRK (UPLO, TRANS, N, K, ZALPHA, ZA, LDA, ZBETA, ZC, LDC)
For all data types, these subprograms set CM
×N to one of the
expressions: C ← αAAT + bC or
C ← αATA + bC. The matrix C is referenced
either by its upper or lower triangular part. The character flags UPLO
and TRANS
determine the part of the matrix used and the operation performed. In subprogram
CSYRK
and ZSYRK,
only values 'N'
or 'T'
are allowed for TRANS;
'C'is
not acceptable.
Rank-k Update, Hermitian
CALL CHERK (UPLO, TRANS, N, K, SALPHA, CA, LDA, SBETA, CC, LDC)
CALL
ZHERK (UPLO,
TRANS,
N,
K,
DALPHA,
ZA,
LDA,
DBETA,
ZC,
LDC)
For all data types, these subprograms set CN × N to one of the expressions:
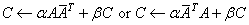
The matrix C is referenced either by its upper or lower triangular part. The character flags UPLO and TRANS determine the part of the matrix used and the operation performed. CAUTION: Notice the scalar parameters α and b are real, and the data in the matrices are complex. Only values 'N'or 'C'are allowed for TRANS; 'T'is not acceptable.
Rank-2k Update, Symmetric
CALL SSYR2K (UPLO, TRANS, N, K, SALPHA, SA, LDA, SB, LDB, SBETA, SC, LDC)
CALL DSYR2K (UPLO, TRANS, N, K, DALPHA, DA, LDA, DB, LDB, DBETA, DC, LDC)
CALL CSYR2K (UPLO, TRANS, N, K, CALPHA, CA, LDA, CB, LDB, CBETA, CC, LDC)
CALL ZSYR2K (UPLO, TRANS, N, K, ZALPHA, ZA, LDA, ZB, LDB, ZBETA, ZC, LDC)
For all data types, these subprograms set CN × N to one of the expressions:
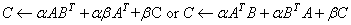
The matrix C is referenced either by its upper or lower triangular part. The character flags UPLO and TRANS determine the part of the matrix used and the operation performed. In subprogram CSYR2K and ZSYR2K, only values 'N'or 'T' are allowed for TRANS; 'C'is not acceptable.
Rank-2k Update, Hermitian
CALL CHER2K (UPLO, TRANS, N, K, CALPHA, CA, LDA, CB, LDB, SBETA, CC, LDC)
CALL ZHER2K (UPLO, TRANS, N, K, ZALPHA, ZA, LDA, ZB, LDB, DBETA, ZC, LDC)
For all data types, these subprograms set CN × N to one of the expressions:

The matrix C is referenced either by its upper or lower triangular part. The character flags UPLO and TRANS determine the part of the matrix used and the operation performed. CAUTION: Notice the scalar parameter b is real, and the data in the matrices are complex. In subprogram CHER2K and ZHER2K, only values 'N' or 'C'are allowed for TRANS; 'T'is not acceptable.
Matrix-Matrix Multiply, Triangular
CALL STRMM (SIDE, UPLO, TRANSA, DIAGNL, M, N, SALPHA, SA, LDA, SB, LDB)
CALL
DTRMM (SIDE,
UPLO,
TRANSA,
DIAGNL,
M,
N,
DALPHA,
DA,
LDA,
DB,
LDB)
CALL CTRMM (SIDE, UPLO, TRANSA, DIAGNL, M, N, CALPHA, CA, LDA, CB,LDB)
CALL
ZTRMM (SIDE,
UPLO,
TRANSA,
DIAGNL,
M,
N,
ZALPHA,
ZA,
LDA,
ZB,
LDB)
For all data types, these subprograms set BM ×N to one of the_expressions:
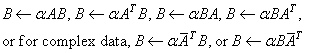
where A is a triangular matrix. The matrix A is either referenced using its upper or lower triangular part and is unit or nonunit triangular. The character flags SIDE, UPLO, TRANSA, and DIAGNL determine the part of the matrix used and the operation performed.
Matrix-Matrix Solve, Triangular
CALL STRSM (SIDE, UPLO, TRANSA, DIAGNL, M, N, SALPHA, SA, LDA, SB, LDB)
CALL
DTRSM (SIDE,
UPLO,
TRANSA,
DIAGNL,
M,
N,
DALPHA,
DA,
LDA,
DB,
LDB)
CALL CTRSM (SIDE, UPLO, TRANSA, DIAGNL, M, N, CALPHA, CA, LDA, CB, LDB)
CALL
ZTRSM (SIDE,
UPLO,
TRANSA,
DIAGNL,
M,
N,
ZALPHA,
ZA,
LDA,
ZB,
LDB)
For all data types, these subprograms set BM ×N to one of the expressions:
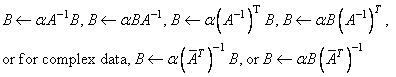
where A is a triangular matrix. The matrix A is either referenced using its upper or lower triangular part and is unit or nonunit triangular. The character flags SIDE, UPLO, TRANSA, and DIAGNL determine the part of the matrix used and the operation performed.
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |