Solves a first order differential-algebraic system of equations, g(t, y, yʹ) = 0, using the Petzold−Gear BDF method.
Required Arguments
T Independent
variable, t. (Input/Output)
Set T to the starting
value t0 at the first step.
TOUT Final
value of the independent variable. (Input)
Update this value
when re-entering after output, IDO = 2.
IDO Flag indicating the state of the computation. (Input/Output)
IDO State
1 Initial entry
2 Normal re-entry after obtaining output
3 Release workspace
4 Return because of an error condition
The user sets IDO = 1 or IDO = 3. All other values of IDO are defined as output. The initial call is made with IDO = 1 and T = t0. The routine then sets IDO = 2, and this value is used for all but the last entry that is made with IDO = 3. This call is used to release workspace and other final tasks. Values of IDO larger than 4 occur only when calling the second-level routine D2SPG and using the options associated with reverse communication.
Y Array of size NEQ containing the dependent variable values, y. This array must contain initial values. (Input/Output)
YPR Array of
size NEQ
containing derivative values, y ʹ. This array must contain
initial values. (Input/Output)
The routine will solve for consistent values
of yʹ to satisfy
the equations at the starting point.
GCN
User-supplied SUBROUTINE to evaluate
g(t, y, yʹ). The usage is
CALL GCN (NEQ, T, Y, YPR, GVAL), where GCN must be declared
EXTERNAL in the
calling program. The routine will solve for values of yʹ(t0) so that
g(t0, y, yʹ) = 0. The user can signal
that g is not defined at requested values of (t, y,
yʹ) using an
option. This causes the routine to reduce the step size or else quit.
NEQ Number of
differential equations. (Input)
T Independent
variable. (Input)
Y Array of size
NEQ containing
the dependent variable values y(t) . (Input)
YPR Array of size
NEQ containing
the derivative values yʹ(t).
(Input)
GVAL
Array of size NEQ containing the
function values, g(t, y, yʹ). (Output)
Optional Arguments
NEQ Number of
differential equations. (Input)
Default: NEQ = size(y,1)
FORTRAN 90 Interface
Generic: CALL DASPG (T, TOUT, IDO, Y, YPR, GCN[, ])
Specific: The specific interface names are S_DASPG and D_DASPG.
FORTRAN 77 Interface
Single: CALL DASPG (NEQ, T, TOUT, IDO, Y, YPR, GCN)
Double: The double precision name is DDASPG.
Description
Routine DASPG finds an approximation to the solution of a system of differential-algebraic equations g(t, y, yʹ) = 0, with given initial data for y and yʹ. The routine uses BDF formulas, appropriate for systems of stiff ODEs, and attempts to keep the global error proportional to a user-specified tolerance. See Brenan et al. (1989). This routine is efficient for stiff systems of index 1 or index 0. See Brenan et al. (1989) for a definition of index. Users are encouraged to use DOUBLE PRECISION accuracy on machines with a short REAL precision accuracy. The examples given below are in REAL accuracy because of the desire for consistency with the rest of IMSL MATH/LIBRARY examples. The routine DASPG is based on the code DASSL designed by L. Petzold (1982-1990).
Comments
Users can often get started using the routine DASPG/DDASPG without reading beyond this point in the documentation. There is often no reason to use options when getting started. Those readers who do not want to use options can turn directly to the first two examples. The following tables give numbers and key phrases for the options. A detailed guide to the options is given below in Comment 2.
|
Value |
Brief or Key Phrase for INTEGER Option |
|
6 |
INTEGER option numbers |
|
7 |
Floating-point option numbers |
|
IN(1) |
First call to DASPG, D2SPG |
|
IN(2) |
Scalar or vector tolerances |
|
IN(3) |
Return for output at intermediate steps |
|
IN(4) |
Creep up on special point, TSTOP |
|
IN(5) |
Provide (analytic) partial derivative formulas |
|
IN(6) |
Maximum number of steps |
|
IN(7) |
Control maximum step size |
|
IN(8) |
Control initial step size |
|
IN(9) |
Not Used |
|
IN(10) |
Constrain dependent variables |
|
IN(11) |
Consistent initial data |
|
IN(12-15) |
Not Used |
|
IN(16) |
Number of equations |
|
IN(17) |
What routine did, if any errors |
|
IN(18) |
Maximum BDF order |
|
IN(19) |
Order of BDF on next move |
|
IN(20) |
Order of BDF on previous move |
|
IN(21) |
Number of steps |
|
IN(22) |
Number of g evaluations |
|
IN(23) |
Number of derivative matrix evaluations |
|
IN(24) |
Number of error test failures |
|
IN(25) |
Number of convergence test failures |
|
IN(26) |
Reverse communiction for g |
|
IN(27) |
Where is g stored? |
|
IN(28) |
Panic flag |
|
IN(29) |
Reverse communication, for partials |
|
IN(30) |
Where are partials stored? |
|
IN(31) |
Reverse communication, for solving |
|
IN(32) |
Not Used |
|
IN(33) |
Where are vector tolerances stored? |
|
IN(34) |
Is partial derivative array allocated? |
|
IN(35) |
User's work arrays sizes are checked |
|
IN(36-50) |
Not used |
Table 1. Key Phrases for Floating-Point Options
|
Value |
Brief or Key Phrase for Floating-Point Option |
|
INR(1) |
Value of t |
|
INR(2) |
Farthest internal t vaue of integration |
|
INR(3) |
Value of TOUT |
|
INR(4) |
A stopping point of integration before TOUT |
|
INR(5) |
Values of two scalars ATOL, RTOL |
|
INR(6) |
Initial step size to use |
|
INR(7) |
Maximum step allowed |
|
INR(8) |
Condition number reciprocal |
|
INR(9) |
Value of cj for partials |
|
INR(10) |
Step size on the next move |
|
INR(11) |
Step size on the previous move |
|
INR(12-20) |
Not Used |
Table 2. Number and Key Phrases for Floating-Point Options
1. Workspace may be explicitly provided, and many of the options utilized by directly calling D2SPG/DD2SPG. The reference is:
CALL D2SPG (N, T, TOUT, IDO, Y, YPR, GCN, JGCN, IWK, WK)
The additional arguments are as follows:
IDO State
5 Return for evaluation of g(t, y, yʹ)
6 Return for evaluation of matrix A = [∂g/∂y + cj∂g/∂yʹ]
7 Return for factorization of the matrix A = [∂g/∂y + cj∂g/∂yʹ]
8 Return for solution of AΔy = Δg
These values of IDO occur only when calling the second-level routine D2SPG and using options associated with reverse communication. The routine D2SPG/DD2SPG is reentered.
GCN A Fortran SUBROUTINE to compute g(t, y, yʹ). This routine is normally provided by the user. That is the default case. The dummy IMSL routine DGSPG/DDGSPG may be used as this argument when g(t, y, yʹ) is evaluated by reverse communication. In either case, a name must be declared in a Fortran EXTERNAL statement. If usage of the dummy IMSL routine is intended, then the name DGSPG/DDGSPG should be specified. The dummy IMSL routine will never be called under this optional usage of reverse communication. An example of reverse communication for evaluation of g is given in Example 4.
JGCN A Fortran SUBROUTINE to compute partial derivatives of g(t, y, yʹ). This routine may be provided by the user. The dummy IMSL routine DJSPG/DDJSPG may be used as this argument when partial derivatives are computed using divided differences. This is the default. The dummy routine is not called under default conditions. If partial derivatives are to be explicitly provided, the routine JGCN must be written by the user or reverse communication can be used. An example of reverse communication for evaluation of the partials is given in Example 4.
If the user writes a routine with the fixed name DJSPG/DDJSPG, then
partial derivatives can be provided while calling DASPG. An option is used to signal that
formulas for partial derivatives are being supplied. This is illustrated in
Example 3. The name of the partial derivative routine must be declared in a
Fortran EXTERNAL statement when calling D2SPG. If usage of
the dummy IMSL routine is intended, then the name DJSPG/DDJSPG should be specified for this EXTERNAL name.
Whenever the user provides partial derivative evaluation formulas, by whatever
means, that must be noted with an option. Usage of the derivative evaluation
routine is
CALL JGCN
(N, T,
Y, YPR,
CJ, PDG,
LDPDG) where
Arg Definition
N Number of equations. (Input)
T Independent variable, t. (Input)
Y Array of size N containing the values of the dependent variables, y. (Input)
YPR Array of size N containing the values of the derivatives, yʹ. (Input)
CJ The value cj used in computing the partial derivatives returned in PDG. (Input)
PDG Array of size LDPDG * N containing the partial derivatives A = [∂g/∂y + cj∂g/∂yʹ]. Each nonzero derivative entry aij is returned in the array location PDG(i, j). The array contents are zero when the routine is called. Thus, only the nonzero derivatives have to be defined in the routine JGCN. (Output)
LDPDG The leading dimension of PDG. Normally, this value is N. It is a value larger than N under the conditions explained in option 16 of LSLRG (Chapter 1, Linear Systems).
JGCN must be declared EXTERNAL in the calling program.
IWK Work array of integer values. The size of this array is 35 + N. The contents of IWK must not be changed from the first call with IDO = 1 until after the final call with IDO = 3.
WK Work ahrray of floating-point values in the working precision. The size of this array is 41 + (MAXORD + 6)N + (N + K)N(1 − L) where K is determined from the values IVAL(3) and IVAL(4) of option 16 of LSLRG (Chapter 1, Linear Systems). The value of L is 0 unless option IN(34) is used to avoid allocation of the array containing the partial derivatives. With the use of this option, L can be set to 1. The contents of array WK must not be changed from the first call with IDO = 1 until after the final call.
2. Integer and Floating-Point Options with Chapter 11 Options Manager
The routine DASPG allows the user access to many interface parameters and internal working variables by the use of options. The options manager subprograms IUMAG and SUMAG/DUMAG (Chapter 11, Utilities), are used to change options from their default values or obtain the current values of required parameters.
Options of type INTEGER:
6 This is the list of numbers used for INTEGER options. Users will typically call this option first to get the numbers, IN(I), I = 1, 50. This option has 50 entries. The default values are IN(I) = I + 50, I = 1, 50.
7 This is the list of numbers used for REAL and DOUBLE PRECISION options. Users will typically call this option first to get the numbers, INR(I), I = 1,20. This option has 20 entries. The default values are INR(I) = I + 50, I = 1, 20.
IN(1) This is the first call to the routine DASPG or D2SPG. Value is 0 for the first call, 1 for further calls. Setting IDO = 1 resets this option to its default. Default value is 0.
IN(2) This flag controls the kind of tolerances to be used for the solution. Value is 0 for scalar values of absolute and relative tolerances applied to all components. Value is 1 when arrays for both these quantities are specified. In this case, use D2SPG. Increase the size of WK by 2*N, and supply the tolerance arrays at the end of WK. Use option IN(33) to specify the offset into WK where the 2N array values are to be placed: all ATOL values are followed by all RTOL values. Also see IN(33). Default value is 0.
IN(3)
This flag controls when the code returns to the user with output values of
y and
yʹ. If the value is 0, it
returns to the user at T = TOUT only. If the
value is 1, it returns to the user at an internal working step. Default value is
0.
IN(4) This flag controls whether the code should integrate past a special point, TSTOP, and then interpolate to get y and yʹat TOUT. If the value is 0, this is permitted. If the value is 1, the code assumes the equations either change on the alternate side of TSTOP or they are undefined there. In this case, the code creeps up to TSTOP in the direction of integration. The value of TSTOP is set with option INR(4). Default value is 0.
IN(5) This flag controls whether partial derivatives are computed using divided onesided differences, or they are to be computed using user-supplied evaluation formulas. If the value is 0, use divided differences. If the value is 1, use formulas for the partial derivatives. See Example 3 for an illustration of one way to do this. Default value is 0.
IN(6) The maximum number of steps. Default value is 500.
IN(7) This flag controls a maximum magnitude constraint for the step size. If the value is 0, the routine picks its own maximum. If the value is 1, a maximum is specified by the user. That value is set with option number INR(7). Default value is 0.
IN(8) This flag controls an initial value for the step size. If the value is 0, the routine picks its own initial step size. If the value is 1, a starting step size is specified by the user. That value is set with option number INR(6). Default value is 0.
IN(9) Not used. Default value is 0.
IN(10) This flag controls attempts to constrain all components to be nonnegative. If the value is 0, no constraints are enforced. If value is 1, constraint is enforced. Default value is 0.
IN(11) This flag controls whether the initial values (t, y, yʹ) are consistent. If the value is 0, g(t, y, yʹ) = 0 at the initial point. If the value is 1, the routine will try to solve for yʹ to make this equation satisfied. Default value is 0.
IN(12-15) Not used. Default value is 0 for each option.
IN(16) The number of equations in the system, n. Default value is 0.
IN(17) This value reports what the routine did. Default value is 0.
|
Value |
Explanation |
|
1 |
A step was taken in the intermediate output mode. The value TOUT has not been reached. |
|
2 |
The integration to exactly TSTOP was completed. |
|
3 |
The integration to TSTOP was completed by stepping past TSTOP and interpolating to evaluate y and yʹ. |
|
−1 |
Too many steps taken. |
|
−2 |
Error tolerances are too small. |
|
−3 |
A pure relative error tolerance can't be satisfied. |
|
−6 |
There were repeated error test failures on the last step. |
|
−7 |
The BDF corrector equation solver did not converge. |
|
−8 |
The matrix of partial derivatives is singular. |
|
−10 |
The BDF corrector equation solver did not converge because the evaluation failure flag was raised. |
|
−11 |
The evaluation failure flag was raised to quit. |
|
−12 |
The iteration for the initial vaule of yʹ did not converge. |
|
−33 |
There is a fatal error, perhaps caused by invalid input. |
Table 3. What the Routine DASPG or D2SPG Did
IN(18) The maximum order of BDF formula the routine should use. Default value is 5.
IN(19) The order of the BDF method the routine will use on the next step. Default value is IMACH(5).
IN(20) The order of the BDF method used on the last step. Default value is IMACH(5).
IN(21) The number of steps taken so far. Default value is 0.
IN(22) The number of times that g has been evaluated. Default value is 0.
IN(23) The number of times that the partial derivative matrix has been evaluated. Default value is 0.
IN(24) The total number of error test failures so far. Default value is 0.
IN(25) The total number of convergence test failures so far. This includes singular iteration matrices. Default value is 0.
IN(26)
Use reverse communication to evaluate g when this value is 0. If the value
is 1, forward communication is used. Use the routine D2SPG for reverse
communication. With reverse communication, a return will be made with
IDO = 5. Compute the
value of g, place it into the array WK at the offset
obtained with option IN(27), and re-enter the routine. Default value is
1.
IN(27) The user is to store the evaluated function g during reverse communication in the work array WK using this value as an offset. Default value is IMACH(5).
IN(28) This value is a panic flag. After an evaluation of g, this value is checked. The value of g is used if the flag is 0. If it has the value −1, the routine reduces the step size and possibly the order of the BDF. If the value is −2, the routine returns control to the user immediately. This option is also used to signal a singular or poorly conditioned partial derivative matrix encountered during the factor phase in reverse communication. Use a nonzero value when the matrix is singular. Default value is 0.
IN(29) Use reverse communication to evaluate the partial derivative matrix when this value is 0. If the value is 1, forward communication is used. Use the routine D2SPG for reverse communication. With reverse communication, a return will be made with IDO = 6. Compute the partial derivative matrix A and re-enter the routine. If forward communication is used for the linear solver, return the partials using the offset into the array WK. This offset value is obtained with option IN(30). Default value is 1.
IN(30) The user is to store the values of the partial derivative matrix A by columns in the work array WK using this value as an offset. The option 16 for LSLRG is used here to compute the row dimension of the internal working array that contains A. Users can also choose to store this matrix in some convenient form in their calling program if they are providing linear system solving using reverse communication. See options IN(31) and IN(34). Default value is IMACH(5).
IN(31)
Use reverse communication to solve the linear system AΔy = Δg if this value is 0.
If the value is 1, use forward communication into the routines L2CRG and LFSRG (Chapter 1, Linear Systems) for the linear system solving.
Return the solution using the offset into the array WK where g is
stored. This offset value is obtained with option IN(27). With reverse
communication, a return will be made with IDO = 7 for
factorization of A and with IDO = 8 for solving
the system. Re-enter the routine in both cases. If the matrix A is singular or
poorly conditioned, raise the panic flag, option IN(28), during the
factorization.
Default value is 1.
IN(32) Not used. Default value is 0.
IN(33) This value is used when IN(2) is set to 1, indicating that arrays of absolute and relative tolerances are input in the WK array of D2SPG. Set this parameter to the offset, ioff, into WK where the tolerances are stored. Increase the size of WK by 2*N , and store tolerance values beginning at ioff=size(WK)-2*N+1. Absolute tolerances will be stored in WK(ioff+i-1) for i=1,N and relative tolerances will be stored in WK(ioff+N+i-1) for i=1,N. Also, use IN(35) to specify the size of the work arrays.
IN(34) This flag is used if the user has not allocated storage for the matrix A in the array WK. If the value is 0, storage is allocated. If the value is 1, storage was not allocated. In this case, the user must be using reverse communication to evaluate the partial derivative matrix and to solve the linear systems AΔy = Δg. Default value is 0.
IN(35) These two values are the sizes of the arrays IWK and WK allocated in the users program. The values are checked against the program requirements. These checks are made only if the values are positive. Users will normally set this option when directly calling D2SPG. Default values are (0, 0).
Options of type REAL or DOUBLE PRECISION:
INR(1) The value of the independent variable, t. Default value is AMACH(6).
INR(2) The farthest working t point the integration has reached. Default value is AMACH(6) .
INR(3) The current value of TOUT. Default value is AMACH(6).
INR(4) The next special point, TSTOP, before reaching TOUT. Default value is AMACH(6). Used with option IN(4).
INR(5) The pair of scalar values ATOL and RTOL that apply to the error estimates of all components of y. Default values for both are SQRT(AMACH(4)).
INR(6) The initial step size if DASPG is not to compute it internally. Default value is AMACH(6).
INR(7) The maximum step size allowed. Default value is AMACH(2).
INR(8) This value is the reciprocal of the condition number of the matrix A. It is defined when forward communication is used to solve for the linear updates to the BDF corrector equation. No further program action, such as declaring a singular system, based on the condition number. Users can declare the system to be singular by raising the panic flag using option IN(28). Default value is AMACH(6).
INR(9) The value of cj used in the partial derivative matrix for reverse communication evaluation. Default value is AMACH(6).
INR(10) The step size to be attempted on the next move. Default value is AMACH(6).
INR(11) The step size taken on the previous move. Default value is AMACH(6).
4. Norm Function Subprogram
The routine DASPG uses a weighted Euclidean-RMS norm to measure the size of the estimated error in each step. This is done using a FUNCTION subprogram: REAL FUNCTION D10PG (N, V, WT). This routine returns the value of the RMS weighted norm given by:
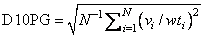
Users can replace this function with one of their own choice. This should be done only for problem-related reasons.
Example 1
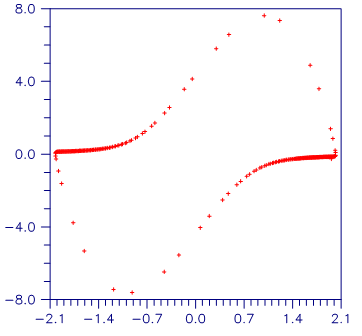
The Van der Pol equation u″ + μ(u2 − 1) uʹ + u = 0, μ > 0, is a single ordinary differential equation with a periodic limit cycle. See Hartman (1964, page 181). For the value μ = 5, the equations are integrated from t = 0 until the limit has clearly developed at t = 26. The (arbitrary) initial conditions used here are u(0) = 2 and uʹ(0) = − 2/3. Except for these initial conditions and the final t value, this is problem (E2) of the Enright and Pryce (1987) test package. This equation is solved as a differential-algebraic system by defining the first-order system:

Note that the initial condition for
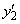
in the sample program is not consistent, g2 ≠ 0 at t = 0. The routine DASPG solves for this starting value. No options need to be changed for this usage. The set of pairs (u(tj), uʹ(tj)) are accumulated for the 260 values tj = 0.1, 26, (0.1).
USE UMACH_INT
USE DASPG_INT
IMPLICIT NONE
INTEGER N, NP, IDO
PARAMETER (N=2, NP=260)
! SPECIFICATIONS FOR LOCAL VARIABLES
INTEGER ISTEP, NOUT, NSTEP
REAL DELT, T, TEND, U(NP), UPR(NP), Y(N), YPR(N)
! SPECIFICATIONS FOR FUNCTIONS
EXTERNAL GCN
! Define initial data
IDO = 1
T = 0.0
TEND = 26.0
DELT = 0.1
NSTEP = TEND/DELT
! Initial values
Y(1) = 2.0
Y(2) = -2.0/3.0
! Initial derivatives
YPR(1) = Y(2)
YPR(2) = 0.
! Write title
CALL UMACH (2, NOUT)
WRITE (NOUT,99998)
! Integrate ODE/DAE
ISTEP = 0
10 CONTINUE
ISTEP = ISTEP + 1
CALL DASPG (T, T+DELT, IDO, Y, YPR, GCN)
! Save solution for plotting
IF (ISTEP .LE. NSTEP) THEN
U(ISTEP) = Y(1)
UPR(ISTEP) = YPR(1)
! Release work space
IF (ISTEP .EQ. NSTEP) IDO = 3
GO TO 10
END IF
WRITE (NOUT,99999) TEND, Y, YPR
99998 FORMAT (11X, 'T', 14X, 'Y(1)', 11X, 'Y(2)', 10X, 'Y''(1)', 10X, &
'Y''(2)')
99999 FORMAT (5F15.5)
! Start plotting
! CALL SCATR (NSTEP, U, UPR)
! CALL EFSPLT (0, ' ')
END
!
SUBROUTINE GCN (N, T, Y, YPR, GVAL)
! SPECIFICATIONS FOR ARGUMENTS
INTEGER N
REAL T, Y(N), YPR(N), GVAL(N)
! SPECIFICATIONS FOR LOCAL VARIABLES
REAL EPS
!
EPS = 0.2
!
GVAL(1) = Y(2) - YPR(1)
GVAL(2) = (1.0-Y(1)**2)*Y(2) - EPS*(Y(1)+YPR(2))
RETURN
END
Output
T
Y(1)
Y(2)
Y'(1)
Y'(2)
26.00000
1.45330
-0.24486
-0.24713 -0.09399
Figure 5- 1 Van der Pol Cycle, (u(t), uʹ (t)), = 5.
Additional Examples
Example 2
The first-order equations of motion of a point-mass
m suspended on a massless wire of length 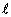 under the influence of
gravity force, mg and tension value λ, in Cartesian coordinates,
(p, q), are
under the influence of
gravity force, mg and tension value λ, in Cartesian coordinates,
(p, q), are
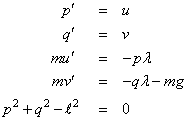
This is a genuine differential-algebraic system. The problem, as stated, has an index number equal to the value 3. Thus, it cannot be solved with DASPG directly. Unfortunately, the fact that the index is greater than 1 must be deduced indirectly. Typically there will be an error processed which states that the (BDF) corrector equation did not converge. The user then differentiates and replaces the constraint equation. This example is transformed to a problem of index number of value 1 by differentiating the last equation twice. This resulting equation, which replaces the given equation, is the total energy balance:
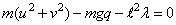
With initial conditions and systematic definitions of the dependent variables, the system becomes:
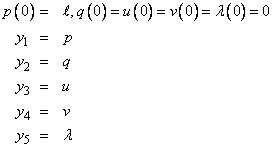

The problem is given in English measurement units of feet,
pounds, and seconds. The wire has length 6.5 ft, and the mass at the end
is 98 lb. Usage of the software does not require it, but standard or SI
units are used in the numerical model. This conversion of units is done as a
first step in the user-supplied evaluation routine, GCN.
A set of initial conditions, corresponding to the pendulum starting in a
horizontal position, are provided as output for the input signal of n =
0. The maximum magnitude of the tension parameter,
λ(t) = y5 (t), is
computed at the output points,
t = 0.1, π, (0.1). This extreme value
is converted to English units and printed.
USE
DASPG_INT
USE
CUNIT_INT
USE DASPG_INT
USE CUNIT_INT
USE UMACH_INT
USE CONST_INT
IMPLICIT NONE
INTEGER N
PARAMETER (N=5)
! SPECIFICATIONS FOR LOCAL VARIABLES
INTEGER IDO, ISTEP, NOUT, NSTEP
REAL DELT, GVAL(N), MAXLB, MAXTEN, T, TEND, TMAX, Y(N), &
YPR(N)
! SPECIFICATIONS FOR INTRINSICS
INTRINSIC ABS
REAL ABS
! SPECIFICATIONS FOR SUBROUTINES
EXTERNAL GCN
! SPECIFICATIONS FOR FUNCTIONS
! Define initial data
IDO = 1
T = 0.0
TEND = CONST('pi')
DELT = 0.1
NSTEP = TEND/DELT
CALL UMACH (2, NOUT)
! Get initial conditions
CALL GCN (0, T, Y, YPR, GVAL)
ISTEP = 0
MAXTEN = 0.
10 CONTINUE
ISTEP = ISTEP + 1
CALL DASPG (T, T+DELT, IDO, Y, YPR, GCN)
IF (ISTEP .LE. NSTEP) THEN
! Note max tension value
IF (ABS(Y(5)) .GT. ABS(MAXTEN)) THEN
TMAX = T
MAXTEN = Y(5)
END IF
IF (ISTEP .EQ. NSTEP) IDO = 3
GO TO 10
END IF
! Convert to English units
CALL CUNIT (MAXTEN, 'kg/s**2', MAXLB, 'lb/s**2')
! Print maximum tension
WRITE (NOUT,99999) MAXLB, TMAX
99999 FORMAT (' Extreme string tension of', F10.2, ' (lb/s**2)', &
' occurred at ', 'time ', F10.2)
END
!
SUBROUTINE GCN (N, T, Y, YPR, GVAL)
USE CUNIT_INT
USE CONST_INT
! SPECIFICATIONS FOR ARGUMENTS
INTEGER N
REAL T, Y(*), YPR(*), GVAL(*)
! SPECIFICATIONS FOR LOCAL VARIABLES
REAL FEETL, GRAV, LENSQ, MASSKG, MASSLB, METERL, MG
! SPECIFICATIONS FOR SAVE VARIABLES
LOGICAL FIRST
SAVE FIRST
! SPECIFICATIONS FOR SUBROUTINES
! SPECIFICATIONS FOR FUNCTIONS
!
DATA FIRST/.TRUE./
!
IF (FIRST) GO TO 20
10 CONTINUE
! Define initial conditions
IF (N .EQ. 0) THEN
! The pendulum is horizontal
! with these initial y values
Y(1) = METERL
Y(2) = 0.
Y(3) = 0.
Y(4) = 0.
Y(5) = 0.
YPR(1) = 0.
YPR(2) = 0.
YPR(3) = 0.
YPR(4) = 0.
YPR(5) = 0.
RETURN
END IF
! Compute residuals
GVAL(1) = Y(3) - YPR(1)
GVAL(2) = Y(4) - YPR(2)
GVAL(3) = -Y(1)*Y(5) - MASSKG*YPR(3)
GVAL(4) = -Y(2)*Y(5) - MASSKG*YPR(4) - MG
GVAL(5) = MASSKG*(Y(3)**2+Y(4)**2) - MG*Y(2) - LENSQ*Y(5)
RETURN
! Convert from English to
! Metric units:
20 CONTINUE
FEETL = 6.5
MASSLB = 98.0
! Change to meters
CALL CUNIT (FEETL, 'ft', METERL, 'meter')
! Change to kilograms
CALL CUNIT (MASSLB, 'lb', MASSKG, 'kg')
! Get standard gravity
GRAV = CONST('StandardGravity')
MG = MASSKG*GRAV
LENSQ = METERL**2
FIRST = .FALSE.
GO TO 10
END
Output
Extreme string tension of 1457.24 (lb/s**2) occurred at time 2.50
Example 3
In this example, we solve a stiff ordinary differential equation (E5) from the test package of Enright and Pryce (1987). The problem is nonlinear with nonreal eigenvalues. It is included as an example because it is a stiff problem, and its partial derivatives are provided in the usersupplied routine with the fixed name DJSPG. Users who require a variable routine name for partial derivatives can use the routine D2SPG. Providing explicit formulas for partial derivatives is an important consideration for problems where evaluations of the function g(t, y, yʹ) are expensive. Signaling that a derivative matrix is provided requires a call to the Chapter 11 options manager utility, IUMAG. In addition, an initial integration step-size is given for this test problem. A signal for this is passed using the options manager routine IUMAG. The error tolerance is changed from the defaults to a pure absolute tolerance of 0.1 * SQRT(AMACH(4)). Also see IUMAG, and SUMAG/DUMAG in Chapter 11, Utilities, for further details about the options manager routines.
USE IMSL_LIBRARIES
IMPLICIT NONE
INTEGER N
PARAMETER (N=4)
! SPECIFICATIONS FOR PARAMETERS
INTEGER ICHAP, IGET, INUM, IPUT, IRNUM
PARAMETER (ICHAP=5, IGET=1, INUM=6, IPUT=2, IRNUM=7)
! SPECIFICATIONS FOR LOCAL VARIABLES
INTEGER IDO, IN(50), INR(20), IOPT(2), IVAL(2), NOUT
REAL C0, PREC, SVAL(3), T, TEND, Y(N), YPR(N)
! SPECIFICATIONS FOR FUNCTIONS
EXTERNAL GCN
! Define initial data
IDO = 1
T = 0.0
TEND = 1000.0
! Initial values
C0 = 1.76E-3
Y(1) = C0
Y(2) = 0.
Y(3) = 0.
Y(4) = 0.
! Initial derivatives
YPR(1) = 0.
YPR(2) = 0.
YPR(3) = 0.
YPR(4) = 0.
! Get option numbers
IOPT(1) = INUM
CALL IUMAG ('math', ICHAP, IGET, 1, IOPT, IN)
IOPT(1) = IRNUM
CALL IUMAG ('math', ICHAP, IGET, 1, IOPT, INR)
! Provide initial step
IOPT(1) = INR(6)
SVAL(1) = 5.0E-5
! Provide absolute tolerance
IOPT(2) = INR(5)
PREC = AMACH(4)
SVAL(2) = 0.1*SQRT(PREC)
SVAL(3) = 0.0
CALL UMAG ('math', ICHAP, IPUT, IOPT, SVAL)
! Using derivatives and
IOPT(1) = IN(5)
IVAL(1) = 1
! providing initial step
IOPT(2) = IN(8)
IVAL(2) = 1
CALL IUMAG ('math', ICHAP, IPUT, 2, IOPT, IVAL)
! Write title
CALL UMACH (2, NOUT)
WRITE (NOUT,99998)
! Integrate ODE/DAE
CALL DASPG (T, TEND, IDO, Y, YPR, GCN)
WRITE (NOUT,99999) T, Y, YPR
! Reset floating options
! to defaults
IOPT(1) = -INR(5)
IOPT(2) = -INR(6)
!
CALL UMAG ('math', ICHAP, IPUT, IOPT, SVAL)
! Reset integer options
! to defaults
IOPT(1) = -IN(5)
IOPT(2) = -IN(8)
!
CALL IUMAG ('math', ICHAP, IPUT, 2, IOPT, IVAL)
99998 FORMAT (11X, 'T', 14X, 'Y followed by Y''')
99999 FORMAT (F15.5/(4F15.5))
END
!
SUBROUTINE GCN (N, T, Y, YPR, GVAL)
! SPECIFICATIONS FOR ARGUMENTS
INTEGER N
REAL T, Y(N), YPR(N), GVAL(N)
! SPECIFICATIONS FOR LOCAL VARIABLES
REAL C1, C2, C3, C4
!
C1 = 7.89E-10
C2 = 1.1E7
C3 = 1.13E9
C4 = 1.13E3
!
GVAL(1) = -C1*Y(1) - C2*Y(1)*Y(3) - YPR(1)
GVAL(2) = C1*Y(1) - C3*Y(2)*Y(3) - YPR(2)
GVAL(3) = C1*Y(1) - C2*Y(1)*Y(3) + C4*Y(4) - C3*Y(2)*Y(3) - &
YPR(3)
GVAL(4) = C2*Y(1)*Y(3) - C4*Y(4) - YPR(4)
RETURN
END
SUBROUTINE DJSPG (N, T, Y, YPR, CJ, PDG, LDPDG)
! SPECIFICATIONS FOR ARGUMENTS
INTEGER N, LDPDG
REAL T, CJ, Y(N), YPR(N), PDG(LDPDG,N)
! SPECIFICATIONS FOR LOCAL VARIABLES
REAL C1, C2, C3, C4
!
C1 = 7.89E-10
C2 = 1.1E7
C3 = 1.13E9
C4 = 1.13E3
!
PDG(1,1) = -C1 - C2*Y(3) - CJ
PDG(1,3) = -C2*Y(1)
PDG(2,1) = C1
PDG(2,2) = -C3*Y(3) - CJ
PDG(2,3) = -C3*Y(2)
PDG(3,1) = C1 - C2*Y(3)
PDG(3,2) = -C3*Y(3)
PDG(3,3) = -C2*Y(1) - C3*Y(2) - CJ
PDG(3,4) = C4
PDG(4,1) = C2*Y(3)
PDG(4,3) = C2*Y(1)
PDG(4,4) = -C4 - CJ
RETURN
END
Output
T
Y followed by Y'
1000.00000
0.00162
0.00000
0.00000 0.00000
0.00000
0.00000 0.00000
0.00000
Example 4
In this final example, we compute the solution of n
= 10 ordinary differential equations,
g = Hy yʹ, where y(0) =
y0= (1, 1,
, 1)T. The value
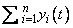
is evaluated at t = 1. The constant matrix H has entries hi, j = min(j − i, 0) so it is lower Hessenberg. We use reverse communication for the evaluation of the following intermediate quantities:
1. The function g,
2. The partial derivative matrix A = ∂g/∂y + cj∂g/∂yʹ = H − cj I,
3. The solution of the linear system AΔy = Δg.
In addition to the use of reverse communication, we evaluate the partial derivatives using formulas. No storage is allocated in the floating-point work array for the matrix. Instead, the matrix A is stored in an array A within the main program unit. Signals for this organization are passed using the routine IUMAG (Chapter 11, Utilities).
An algorithm appropriate for this matrix, Givens transformations applied from the right side, is used to factor the matrix A. The rotations are reconstructed during the solve step. See SROTG (Chapter 9, Basic Matrix/Vector Operations) for the formulas.
The routine D2SPG stores the value of cj. We get it with a call to the options manager routine SUMAG (Chapter 11, Utilities). A pointer, or offset into the work array, is obtained as an integer option. This gives the location of g and Δg. The solution vector Δy replaces Δg at that location. Caution: If a user writes code wherein g is computed with reverse communication and partials are evaluated with divided differences, then there will be two distinct places where g is to be stored. This example shows a correct place to get this offset.
This example also serves as a prototype for large, structured (possibly nonlinear) DAE problems where the user must use special methods to store and factor the matrix A and solve the linear system AΔy = Δg. The word factor is used literally here. A user could, for instance, solve the system using an iterative method. Generally, the factor step can be any preparatory phase required for a later solve step.
USE IMSL_LIBRARIES
IMPLICIT NONE
INTEGER N
PARAMETER (N=10)
! SPECIFICATIONS FOR PARAMETERS
INTEGER ICHAP, IGET, INUM, IPUT, IRNUM
PARAMETER (ICHAP=5, IGET=1, INUM=6, IPUT=2, IRNUM=7)
! SPECIFICATIONS FOR LOCAL VARIABLES
INTEGER I, IDO, IN(50), INR(20), IOPT(6), IVAL(7), IWK(35+N), &
J, NOUT
REAL A(N,N), GVAL(N), H(N,N), SC, SS, SUMY, SVAL(1), T, &
TEND, WK(41+11*N), Y(N), YPR(N), Z
! SPECIFICATIONS FOR INTRINSICS
INTRINSIC ABS, SQRT
REAL ABS, SQRT
! SPECIFICATIONS FOR SUBROUTINES
! SPECIFICATIONS FOR FUNCTIONS
EXTERNAL DGSPG, DJSPG
! Define initial data
IDO = 1
T = 0.0E0
TEND = 1.0E0
! Initial values
CALL SSET (N, 1.0E0, Y, 1)
CALL SSET (N, 0.0, YPR, 1)
! Initial lower Hessenberg matrix
CALL SSET (N*N, 0.0E0, H, 1)
DO 20 I=1, N - 1
DO 10 J=1, I + 1
H(I,J) = J - I
10 CONTINUE
20 CONTINUE
DO 30 J=1, N
H(N,J) = J - N
30 CONTINUE
! Get integer option numbers
IOPT(1) = INUM
CALL IUMAG ('math', ICHAP, IGET, 1, IOPT, IN)
! Get floating point option numbers
IOPT(1) = IRNUM
CALL IUMAG ('math', ICHAP, IGET, 1, IOPT, INR)
! Set for reverse communication
! evaluation of g.
IOPT(1) = IN(26)
IVAL(1) = 0
! Set for evaluation of partial
! derivatives.
IOPT(2) = IN(5)
IVAL(2) = 1
! Set for reverse communication
! evaluation of partials.
IOPT(3) = IN(29)
IVAL(3) = 0
! Set for reverse communication
! solution of linear equations.
IOPT(4) = IN(31)
IVAL(4) = 0
! Storage for the partial
! derivative array not allocated.
IOPT(5) = IN(34)
IVAL(5) = 1
! Set the sizes of IWK, WK
! for internal checking.
IOPT(6) = IN(35)
IVAL(6) = 35 + N
IVAL(7) = 41 + 11*N
! 'Put' integer options.
CALL IUMAG ('math', ICHAP, IPUT, 6, IOPT, IVAL)
! Write problem title.
CALL UMACH (2, NOUT)
WRITE (NOUT,99998)
! Integrate ODE/DAE. Use
! dummy IMSL external names.
40 CONTINUE
CALL D2SPG (N, T, TEND, IDO, Y, YPR, DGSPG, DJSPG, IWK, WK)
! Find where g goes.
! (It only goes in one place
! here, but can vary if
! divided differences are used
! for partial derivatives.)
IOPT(1) = IN(27)
CALL IUMAG ('math', ICHAP, IGET, 1, IOPT, IVAL)
! Direct user response.
GO TO (50, 180, 60, 50, 90, 100, 130, 150), IDO
50 CONTINUE
! This should not occur.
WRITE (NOUT,*) ' Unexpected return with IDO = ', IDO
60 CONTINUE
! Reset options to defaults
DO 70 I=1, 50
IN(I) = -IN(I)
70 CONTINUE
CALL IUMAG ('math', ICHAP, IPUT, 50, IN, IVAL)
DO 80 I=1, 20
INR(I) = -INR(I)
80 CONTINUE
CALL UMAG ('math', ICHAP, IPUT, INR, SVAL, numopts=1)
STOP
90 CONTINUE
! Return came for g evaluation.
CALL SCOPY (N, YPR, 1, GVAL, 1)
CALL SGEMV ('NO', N, N, 1.0E0, H, N, Y, 1, -1.0E0, GVAL, 1)
! Put g into place.
CALL SCOPY (N, GVAL, 1, WK(IVAL(1:)), 1)
GO TO 40
100 CONTINUE
! Return came for partial
! derivative evaluation.
110 CALL SCOPY (N*N, H, 1, A, 1)
! Get value of c_j for partials.
IOPT(1) = INR(9)
CALL UMAG ('math', ICHAP, IGET, IOPT, SVAL, numopts=1)
! Subtract c_j from diagonals
! to compute (partials for y')*c_j.
DO 120 I=1, N
A(I,I) = A(I,I) - SVAL(1)
120 CONTINUE
GO TO 40
130 CONTINUE
! Return came for factorization
DO 140 J=1, N - 1
! Construct and apply Givens
! transformations.
CALL SROTG (A(J,J), A(J,J+1), SC, SS)
CALL SROT (N-J, A((J+1):,1), 1, A((J+1):,J+1), 1, SC, SS)
140 CONTINUE
GO TO 40
150 CONTINUE
! Return came to solve the system
CALL SCOPY (N, WK(IVAL(1)), 1, GVAL, 1)
DO 160 J=1, N - 1
GVAL(J) = GVAL(J)/A(J,J)
CALL SAXPY (N-J, -GVAL(J), A((J+1):,J), 1, GVAL((J+1):, 1))
160 CONTINUE
GVAL(N) = GVAL(N)/A(N,N)
! Reconstruct Givens rotations
DO 170 J=N - 1, 1, -1
Z = A(J,J+1)
IF (ABS(Z) .LT. 1.0E0) THEN
SC = SQRT(1.0E0-Z**2)
SS = Z
ELSE IF (ABS(Z) .GT. 1.0E0) THEN
SC = 1.0E0/Z
SS = SQRT(1.0E0-SC**2)
ELSE
SC = 0.0E0
SS = 1.0E0
END IF
CALL SROT (1, GVAL(J:), 1, GVAL((J+1):), 1, SC, SS)
170 CONTINUE
CALL SCOPY (N, GVAL, 1, WK(IVAL(1)), 1)
GO TO 40
!
180 CONTINUE
SUMY = 0.E0
DO 190 I=1, N
SUMY = SUMY + Y(I)
190 CONTINUE
WRITE (NOUT,99999) TEND, SUMY
! Finish up internally
IDO = 3
GO TO 40
99998 FORMAT (11X, 'T', 6X, 'Sum of Y(i), i=1,n')
99999 FORMAT (2F15.5)
END
Output
T Sum of Y(i),
i=1,n
1.00000 65.17058
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |