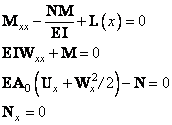BVPMS

Solves a (parameterized) system of differential equations with boundary conditions at two points, using a multiple-shooting method.

Required Arguments

FCNEQN — User-supplied SUBROUTINE to evaluate derivatives. The usage is CALL FCNEQN (NEQNS, T, Y, P, DYDT), where

            NEQNS – Number of equations.   (Input)
T – Independent variable, t.   (Input)
Y – Array of length NEQNS containing the dependent variable.   (Input)
P – Continuation parameter used in solving highly nonlinear problems.   (Input)
See Comment 4.
DYDT – Array of length NEQNS containing yʹ at T.   (Output)

The name FCNEQN must be declared EXTERNAL in the calling program.

FCNJAC — User-supplied SUBROUTINE to evaluate the Jacobian. The usage is CALL FCNJAC (NEQNS, T, Y, P, DYPDY), where

     NEQNS – Number of equations.   (Input)
T – Independent variable.   (Input)
Y – Array of length NEQNS containing the dependent variable.   (Input)
P – Continuation parameter used in solving highly nonlinear problems.   (Input)
See Comment 4.
DYPDY – Array of size NEQNS by NEQNS containing the Jacobian.   (Output)
The entry DYPDY(i, j) contains the partial derivative ∂ fi∕∂ yj evaluated at (t, y).

The name FCNJAC must be declared EXTERNAL in the calling program.

FCNBC — User-supplied SUBROUTINE to evaluate the boundary conditions. The usage is CALL FCNBC (NEQNS, YLEFT, YRIGHT, P, H), where

            NEQNS – Number of equations.   (Input)
YLEFT – Array of length NEQNS containing the values of Y at TLEFT.   (Input)
YRIGHT – Array of length NEQNS containing the values of Y at
TRIGHT.   (Input)
P – Continuation parameter used in solving highly nonlinear problems.   (Input)
See Comment 4.
H – Array of length NEQNS containing the boundary function values.   (Output)
The computed solution satisfies (within BTOL) the conditions hi = 0, i = 1, …, NEQNS.

The name FCNBC must be declared EXTERNAL in the calling program.

TLEFT — The left endpoint. (Input)

TRIGHT — The right endpoint. (Input)

NMAX — Maximum number of shooting points to be allowed. (Input)
If NINIT is nonzero, then NMAX must equal NINIT. It must be at least 2.

NFINAL — Number of final shooting points, including the endpoints. (Output)

TFINAL — Vector of length NMAX containing the final shooting points. (Output)
Only the first NFINAL points are significant.

YFINAL — Array of size NEQNS by NMAX containing the values of Y at the points in TFINAL. (Output)

Optional Arguments

NEQNS — Number of differential equations. (Input)

DTOL — Differential equation error tolerance. (Input)
An attempt is made to control the local error in such a way that the global error is proportional to DTOL.
Default: DTOL = 1.0e-4.

BTOL — Boundary condition error tolerance. (Input)
The computed solution satisfies the boundary conditions, within BTOL tolerance.
Default: BTOL = 1.0e-4.

MAXIT — Maximum number of Newton iterations allowed. (Input)
Iteration stops if convergence is achieved sooner. Suggested values are MAXIT = 2 for linear problems and MAXIT = 9 for nonlinear problems.
Default: MAXIT = 9.

NINIT — Number of shooting points supplied by the user. (Input)
It may be 0. A suggested value for the number of shooting points is 10.
Default: NINIT = 0.

TINIT — Vector of length NINIT containing the shooting points supplied by the user. (Input)
If NINIT = 0, then TINIT is not referenced and the routine chooses all of the shooting points. This automatic selection of shooting points may be expensive and should only be used for linear problems. If NINIT is nonzero, then the points must be an increasing sequence with TINIT(1) = TLEFT and TINIT(NINIT) = TRIGHT. By default, TINIT is not used.

YINIT — Array of size NEQNS by NINIT containing an initial guess for the values of Y at the points in TINIT. (Input)
YINIT is not referenced if NINIT = 0. By default, YINIT is not used.

LDYINI — Leading dimension of YINIT exactly as specified in the dimension statement of the calling program. (Input)
Default: LDYINI = size (YINIT ,1).

LDYFIN — Leading dimension of YFINAL exactly as specified in the dimension statement of the calling program. (Input)
Default: LDYFIN = size (YFINAL,1).

FORTRAN 90 Interface

Generic: CALL BVPMS (FCNEQN, FCNJAC, FCNBC, TLEFT, TRIGHT, NMAX, NFINAL, TFINAL, YFINAL [,…])

Specific: The specific interface names are S_BVPMS and D_BVPMS.

FORTRAN 77 Interface

Single: CALL BVPMS (FCNEQN, FCNJAC, FCNBC, NEQNS, TLEFT, TRIGHT, DTOL, BTOL, MAXIT, NINIT, TINIT, YINIT, LDYINI, NMAX, NFINAL, TFINAL, YFINAL, LDYFIN)

Double: The double precision name is DBVPMS.

Description

Define N = NEQNS, M = NFINAL, ta = TLEFT and tb = TRIGHT. The routine BVPMS uses a multiple-shooting technique to solve the differential equation system yʹ = f (t, y) with boundary conditions of the form

hk(y1 (ta), …, yN (ta), y1 (tb), …, yN (tb)) = 0 for k = 1, …, N

A modified version of IVPRK is used to compute the initial-value problem at each “shot.” If there are M shooting points (including the endpoints ta and tb), then a system of NM simultaneous nonlinear equations must be solved. Newton's method is used to solve this system, which has a Jacobian matrix with a “periodic band” structure. Evaluation of the NM functions and the
NM × NM (almost banded) Jacobian for one iteration of Newton's method is accomplished in one pass from ta to tb of the modified IVPRK, operating on a system of N(N + 1) differential equations. For most problems, the total amount of work should not be highly dependent on M. Multiple shooting avoids many of the serious ill-conditioning problems that plague simple shooting methods. For more details on the algorithm, see Sewell (1982).

The boundary functions should be scaled so that all components hk are of comparable magnitude since the absolute error in each is controlled.

Comments

1. Workspace may be explicitly provided, if desired, by use of B2PMS/DB2PMS. The reference is:

CALL B2PMS (FCNEQN, FCNJAC, FCNBC, NEQNS, TLEFT, TRIGHT, DTOL, BTOL, MAXIT, NINIT, TINIT, YINIT, LDYINI, NMAX, NFINAL, TFINAL, YFINAL, LDYFIN, WORK, IWK)

The additional arguments are as follows:

WORK — Work array of length NEQNS * (NEQNS + 1)(NMAX + 12) +
NEQNS + 30.

IWK — Work array of length NEQNS.

2. Informational errors

Type Code

1 5 Convergence has been achieved; but to get acceptably accurate approximations to y(t), it is often necessary to start an initial-value solver, for example IVPRK, at the nearest TFINAL(i) point to t with t ≥ TFINAL (i). The vectors YFINAL(j, i), j = 1, …, NEQNS are used as the initial values.

4 1 The initial-value integrator failed. Relax the tolerance DTOL or see Comment 3.

4 2 More than NMAX shooting points are needed for stability.

4 3 Newton's iteration did not converge in MAXIT iterations. If the problem is linear, do an extra iteration. If this error still occurs, check that the routine FCNJAC is giving the correct derivatives. If this does not fix the problem, see Comment 3.

4 4 Linear-equation solver failed. The problem may not have a unique solution, or the problem may be highly nonlinear. In the latter case, see Comment 3.

3. Many linear problems will be successfully solved using program-selected shooting points. Nonlinear problems may require user effort and input data. If the routine fails, then increase NMAX or parameterize the problem. With many shooting points the program essentially uses a finite-difference method, which has less trouble with nonlinearities than shooting methods. After a certain point, however, increasing the number of points will no longer help convergence. To parameterize the problem, see Comment 4.

4. If the problem to be solved is highly nonlinear, then to obtain convergence it may be necessary to embed the problem into a one-parameter family of boundary value problems, yʹ = f(t, y, p), h(y(ta, tb, p)) = 0 such that for p = 0, the problem is simple, e.g., linear; and for p = 1, the stated problem is solved. The routine BVPMS/DBVPMS automatically moves the parameter from p = 0 toward p = 1.

5. This routine is not recommended for stiff systems of differential equations.

Example

The differential equations that model an elastic beam are (see Washizu 1968, pages 142−143):

where U is the axial displacement, W is the transverse displacement, N is the axial force, M is the bending moment, E is the elastic modulus, I is the moment of inertia, A0 is the cross-sectional area, and L(x) is the transverse load.

Assume we have a clamped cylindrical beam of radius 0.1in, a length of 10in, and an elastic modulus E = 10.6 × 106 lb/in2. Then, I = 0.784 × 10-4, and A0= π10-2 in2, and the boundary conditions are U = W = Wx= 0 at each end. If we let y1= U, y2 = N/EA0, y3 = W, y4 = Wx,
y5= M/EI , and y6 = Mx/EI, then the above nonlinear equations can be written as a system of six first-order equations.

The boundary conditions are y1 = y3 = y4 = 0 at x = 0 and at x = 10. The loading function is
L(x) = −2, if 3 ≤ x ≤ 7, and is zero elsewhere.

The material parameters, A0 = A0, I = AI, and E, are passed to the evaluation subprograms using the common block PARAM.

USE BVPMS_INT

USE UMACH_INT

IMPLICIT NONE

INTEGER LDY, NEQNS, NMAX

PARAMETER (NEQNS=6, NMAX=21, LDY=NEQNS)

! SPECIFICATIONS FOR LOCAL VARIABLES

INTEGER I, MAXIT, NFINAL, NINIT, NOUT

REAL TOL, X(NMAX), XLEFT, XRIGHT, Y(LDY,NMAX)

! SPECIFICATIONS FOR COMMON /PARAM/

COMMON /PARAM/ A0, A1, E

REAL A0, A1, E

! SPECIFICATIONS FOR INTRINSICS

INTRINSIC REAL

REAL REAL

! SPECIFICATIONS FOR SUBROUTINES

EXTERNAL FCNBC, FCNEQN, FCNJAC

! Set material parameters

A0 = 3.14E-2

A1 = 0.784E-4

E = 10.6E6

! Set parameters for BVPMS

XLEFT = 0.0

XRIGHT = 10.0

MAXIT = 19

NINIT = NMAX

Y = 0.0E0

! Define the shooting points

DO 10 I=1, NINIT

X(I) = XLEFT + REAL(I-1)/REAL(NINIT-1)*(XRIGHT-XLEFT)

10 CONTINUE

! Solve problem

CALL BVPMS (FCNEQN, FCNJAC, FCNBC, XLEFT, XRIGHT, NMAX, NFINAL, &

X, Y, MAXIT=MAXIT, NINIT=NINIT, TINIT=X, YINIT=Y)

! Print results

CALL UMACH (2, NOUT)

WRITE (NOUT,'(26X,A/12X,A,10X,A,7X,A)') 'Displacement', &

'X', 'Axial', 'Transvers'// &

'e'

WRITE (NOUT,'(F15.1,1P2E15.3)') (X(I),Y(1,I),Y(3,I),I=1,NFINAL)

END

SUBROUTINE FCNEQN (NEQNS, X, Y, P, DYDX)

! SPECIFICATIONS FOR ARGUMENTS

INTEGER NEQNS

REAL X, P, Y(NEQNS), DYDX(NEQNS)

! SPECIFICATIONS FOR LOCAL VARIABLES

REAL FORCE

! SPECIFICATIONS FOR COMMON /PARAM/

COMMON /PARAM/ A0, A1, E

REAL A0, A1, E

! Define derivatives

FORCE = 0.0

IF (X.GT.3.0 .AND. X.LT.7.0) FORCE = -2.0

DYDX(1) = Y(2) - P*0.5*Y(4)**2

DYDX(2) = 0.0

DYDX(3) = Y(4)

DYDX(4) = -Y(5)

DYDX(5) = Y(6)

DYDX(6) = P*A0*Y(2)*Y(5)/A1 - FORCE/E/A1

RETURN

END

SUBROUTINE FCNBC (NEQNS, YLEFT, YRIGHT, P, F)

! SPECIFICATIONS FOR ARGUMENTS

INTEGER NEQNS

REAL P, YLEFT(NEQNS), YRIGHT(NEQNS), F(NEQNS)

! SPECIFICATIONS FOR COMMON /PARAM/

COMMON /PARAM/ A0, A1, E

REAL A0, A1, E

! Define boundary conditions

F(1) = YLEFT(1)

F(2) = YLEFT(3)

F(3) = YLEFT(4)

F(4) = YRIGHT(1)

F(5) = YRIGHT(3)

F(6) = YRIGHT(4)

RETURN

END

SUBROUTINE FCNJAC (NEQNS, X, Y, P, DYPDY)

! SPECIFICATIONS FOR ARGUMENTS

INTEGER NEQNS

REAL X, P, Y(NEQNS), DYPDY(NEQNS,NEQNS)

! SPECIFICATIONS FOR COMMON /PARAM/

COMMON /PARAM/ A0, A1, E

REAL A0, A1, E

! SPECIFICATIONS FOR SUBROUTINES

! Define partials, d(DYDX)/dY

DYPDY = 0.0E0

DYPDY(1,2) = 1.0

DYPDY(1,4) = -P*Y(4)

DYPDY(3,4) = 1.0

DYPDY(4,5) = -1.0

DYPDY(5,6) = 1.0

DYPDY(6,2) = P*Y(5)*A0/A1

DYPDY(6,5) = P*Y(2)*A0/A1

RETURN

END

Output

                 Displacement
X          Axial       Transverse
0.0      1.631E-11     -8.677E-10
5.0      1.914E-05     -1.273E-03
10.0      2.839E-05     -4.697E-03
15.0      2.461E-05     -9.688E-03
20.0      1.008E-05     -1.567E-02
25.0    -9.550E-06     -2.206E-02
30.0     -2.721E-05     -2.830E-02
35.0     -3.644E-05     -3.382E-02
40.0     -3.379E-05     -3.811E-02
45.0     -2.016E-05     -4.083E-02
50.0     -4.414E-08     -4.176E-02
55.0      2.006E-05     -4.082E-02
60.0      3.366E-05     -3.810E-02
65.0      3.627E-05     -3.380E-02
70.0      2.702E-05     -2.828E-02
75.0      9.378E-06     -2.205E-02
80.0     -1.021E-05     -1.565E-02
85.0     -2.468E-05     -9.679E-03
90.0     -2.842E-05     -4.692E-03
95.0     -1.914E-05     -1.271E-03
100.0      0.000E+00      0.000E+00

Visual Numerics, Inc.
Visual Numerics - Developers of IMSL and PV-WAVE
http://www.vni.com/
PHONE: 713.784.3131
FAX:713.781.9260