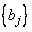Computes the Discrete Fourier Transform (DFT) of a rank-1 complex array, x.
Required Arguments
No required arguments; pairs of optional arguments are required. These pairs are forward_in and forward_out or inverse_in and inverse_out.
Optional Arguments
forward_in =
x (Input)
Stores the input complex array of rank-1 to be
transformed.
forward_out =
y (Output)
Stores the output complex array of rank-1
resulting from the transform.
inverse_in =
y (Input)
Stores the input complex array of rank-1 to be
inverted.
inverse_out =
x (Output)
Stores the output complex array of rank-1
resulting from the inverse transform.
ndata = n
(Input)
Uses the sub-array of size n for the
numbers.
Default value: n = size(x).
ido = ido
(Input/Output)
Integer flag that directs user action. Normally, this argument
is used only when the working variables required for the transform and its
inverse are saved in the calling program unit. Computing the working variables
and saving them in internal arrays within fast_dft is the default. This
initialization step is expensive.
There is a two-step process to compute the working variables just once. Example 3 illustrates this usage. The general algorithm for this usage is to enter fast_dft with ido = 0. A return occurs thereafter with ido < 0. The optional rank-1 complex array w(:) with size(w) >= -ido must be re-allocated. Then, re-enter fast_dft. The next return from fast_dft has the output value ido = 1. The variables required for the transform and its inverse are saved in w(:). Thereafter, when the routine is entered with ido = 1 and for the same value of n, the contents of w(:) will be used for the working variables. The expensive initialization step is avoided. The optional arguments “ido=” and “work_array=” must be used together.
work_array =
w(:) (Output/Input)
Complex array of rank-1 used to store
working variables and values between calls to fast_dft. The value
for size(w) must be at least as
large as the value - ido for the value of
ido < 0.
iopt =
iopt(:) (Input/Output)
Derived type array with the same
precision as the input array; used for passing optional data to fast_dft. The options
are as follows:
|
| |||
iopt(IO) =
?_options(?_fast_dft_scan_for_NaN, ?_dummy)
Examines each input array
entry to find the first value such that
isNaN(x(i)) ==.true.
See the isNaN() function,
Chapter 10.
Default: Does not scan for NaNs.
iopt(IO) =
?_options(?_fast_dft_near_power_of_2, ?_dummy)
Nearest power of 2 ≥
n is returned as an output in iopt(IO + 1)%idummy.
iopt(IO) = ?_options(?_fast_dft_scale_forward, real_part_of_scale)
iopt(IO+1) =
?_options(?_dummy, imaginary_part_of_scale)
Complex number defined by
the factor
cmplx(real_part_of_scale,
imaginary_part_of_scale) is
multiplied by the forward transformed
array.
Default value is 1.
iopt(IO) = ?_options(?_fast_dft_scale_inverse, real_part_of_scale)
iopt(IO+1) =
?_options(?_dummy, imaginary_part_of_scale)
Complex number defined by
the factor
cmplx(real_part_of_scale,
imaginary_part_of_scale) is
multiplied by the inverse transformed
array.
Default value is 1.
FORTRAN 90 Interface
Specific: The specific interface names are S_FAST_DFT, D_FAST_DFT, C_FAST_DFT, and Z_FAST_DFT.
Description
The fast_dft routine is a Fortran 90 version of the FFT suite of IMSL (1994, pp. 772-776). The maximum computing efficiency occurs when the size of the array can be factored in the form
using non-negative integer values {i1, i2, i3, i4}. There is no further restriction on n ≥ 1.
Fatal and Terminal Messages
See the messages.gls file for error messages for FAST_DFT. These error messages are numbered 651-661; 701-711.
Example 1: Transforming an Array of Random Complex Numbers
An array of random complex numbers is obtained. The transform of the numbers is inverted and the final results are compared with the input array.
! This is Example 1 for FAST_DFT.
real(kind(1e0)), parameter :: one=1e0
complex(kind(1e0)), dimension(n) :: a, b, c
! Generate a random complex sequence.
a = cmplx(y(1:n),y(n+1:2*n),kind(one))
! Transform and then invert the sequence back.
call c_fast_dft(forward_in=a, &
call c_fast_dft(inverse_in=b, &
! Check that inverse(transform(sequence)) = sequence.
err = maxval(abs(c-a))/maxval(abs(c))
if (err <= sqrt(epsilon(one))) then
write (*,*) 'Example 1 for FAST_DFT is correct.'
Output
Example 1 for FAST_DFT is correct.
Additional Examples
.p>.F90CH3.DOC!EX2_FAST_DFT;Example 2: Cyclical Data with a Linear Trend
This set of data is sampled from a function x(t) = at + b + y(t), where y(t) is a harmonic series. The independent variable is normalized as -1≤ t ≤ 1. Thus, the data is said to have cyclical components plus a linear trend. As a first step, the linear terms are effectively removed from the data using the least-squares system solver lin_sol_lsq, Chapter 1. Then, the residuals are transformed and the resulting frequencies are analyzed.
! This is Example 2 for FAST_DFT.
integer, parameter :: n=64, k=4
real(kind(1e0)), parameter :: one=1e0, two=2e0, zero=0e0
real(kind(1e0)) y(k), z(2), indx(k), t(n), temp(n)
complex(kind(1e0)) a_trend(n,2), a, b_trend(n,1), b, c(k), f(n),&
! Generate random data for linear trend and harmonic series.
! This emphasizes harmonics 2 through k+1.
! Determine sampling interval.
t=(/(-one+i*delta_t, i=0,n-1)/)
! Make up data set as a linear trend plus harmonics.
matmul(exp(cmplx(zero,spread(t,2,k)*spread(indx,1,n),kind(one))),c)
! Define least-squares matrix data for a linear trend.
call lin_sol_lsq(a_trend, b_trend, x_trend)
r = x - reshape(matmul(a_trend,x_trend),(/n/))
! Transform harmonic residuals.
call c_fast_dft(forward_in=r, forward_out=f)
! The dominant frequencies should be 2 through k+1.
! Sort the magnitude of the transform first.
call s_sort_real(-(abs(f)), temp, iperm=ip)
! The dominant frequencies are output in ip(1:k).
! Sort these values to compare with 2 through k+1.
call s_sort_real(real(ip(1:k)), temp)
if (count(int(temp(1:k)) /= ip(1:k)) == 0) then
write (*,*) 'Example 2 for FAST_DFT is correct.'
Output
Example 2 for FAST_DFT is correct.
.p>.F90CH3.DOC!EX3_FAST_DFT;Example 3: Several Transforms with Initialization
In this example, the optional arguments ido and work_array are used to save working variables in the calling program unit. This results in maximum efficiency of the transform and its inverse since the working variables do not have to be precomputed following each entry to routine fast_dft.
! This is Example 3 for FAST_DFT.
! The value of the array size for work(:) is computed in the
! routine fast_dft as a first step.
complex(kind(1e0)), dimension(n) :: a, b, save_a
complex(kind(1e0)), allocatable :: work(:)
! Generate a random complex array.
a = cmplx(y(1:n),y(n+1:2*n),kind(one))
! Transform and then invert the sequence using the pre-computed
if(allocated(work)) deallocate(work)
! Allocate the space required for work(:).
if (ido_value <= 0) allocate(work(-ido_value))
call c_fast_dft(forward_in=a, forward_out=b, &
ido=ido_value, work_array=work)
! Re-enter routine with working values available in work(:).
call c_fast_dft(inverse_in=b, inverse_out=a, &
ido=ido_value, work_array=work)
! Deallocate the space used for work(:).
if (allocated(work)) deallocate(work)
err = maxval(abs(save_a-a))/maxval(abs(save_a))
if (err <= sqrt(epsilon(one))) then
write (*,*) 'Example 3 for FAST_DFT is correct.'
Output
Example 3 for FAST_DFT is correct.
.p>.F90CH3.DOC!EX4_FAST_DFT;Example 4: Convolutions using Fourier Transforms
In this example we compute sums
The definition implies a matrix-vector product. A
direct approach requires about 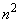 operations consisisting of an add and multiply. An
efficient method consisting of computing the products of the transforms of the
operations consisisting of an add and multiply. An
efficient method consisting of computing the products of the transforms of the
then inverting this product, is preferable to the matrix-vector approach for large problems. The example is also illustrated in operator_ex37, Chapter 10 using the generic function interface FFT and IFFT.
! This is Example 4 for FAST_DFT.
real(kind(1e0)), dimension(n) :: x, y, yy(n,n)
complex(kind(1e0)), dimension(n) :: a, b, c, d, e, f
! Generate two random complex sequence 'a' and 'b'.
! Compute the convolution 'c' of 'a' and 'b'.
! Use matrix times vector for test results.
! Transform the 'a' and 'b' sequences into 'd' and 'e'.
call c_fast_dft(forward_in=a, &
call c_fast_dft(forward_in=b, &
call c_fast_dft(inverse_in=d*e, &
! Check the Convolution Theorem:
! inverse(transform(a)*transform(b)) = convolution(a,b).
err = maxval(abs(c-f))/maxval(abs(c))
if (err <= sqrt(epsilon(one))) then
write (*,*) 'Example 4 for FAST_DFT is correct.'
Output
Example 4 for FAST_DFT is correct.
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |
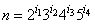

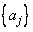 and
and