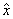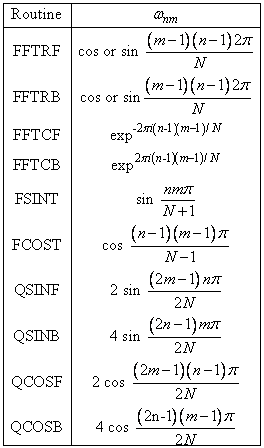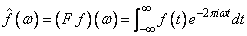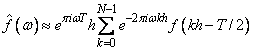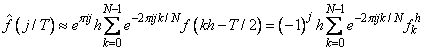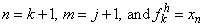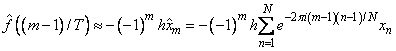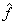Fast Fourier Transforms
A Fast Fourier Transform (FFT) is simply a discrete Fourier
transform that can be computed efficiently. Basically, the straightforward
method for computing the Fourier transform takes approximately N2 operations where
N is the number of points in the transform, while the FFT (which computes
the same values) takes approximately N log N operations. The
algorithms in this chapter are modeled on the Cooley-Tukey (1965) algorithm;
hence, the computational savings occur, not for all integers N, but for
N which are highly composite. That is, N (or in certain cases
N + 1 or N - 1) should be a
product of small primes.
All of the FFT routines compute a discrete Fourier transform. The routines accept a vector x of length N and return a vector
The various transforms are determined by the selection of ω. In the following table, we indicate the selection of ω for the various transforms. This table should not be mistaken for a definition since the precise transform definitions (at times) depend on whether N or m is even or odd.
For many of the routines listed above, there is a corresponding “I” (for initialization) routine. Use these routines only when repeatedly transforming sequences of the same length. In this situation, the “I” routine will compute the initial setup once, and then the user will call the corresponding “2” routine. This can result in substantial computational savings. For more information on the usage of these routines, the user should consult the documentation under the appropriate routine name.
In addition to the one-dimensional transformations described above, we also provide complex two and three-dimensional FFTs and their inverses based on calls to either FFTCF or FFTCB. If you need a higher dimensional transform, then you should consult the example program for FFTCI, which suggests a basic strategy one could employ.
Continuous versus Discrete Fourier Transform
There is, of course, a close connection between the discrete Fourier transform and the continuous Fourier transform. Recall that the continuous Fourier transform is defined (Brigham, 1974) as
We begin by making the following approximation:
If we approximate the last integral using the rectangle rule with spacing h = T/N, we have
Finally, setting ω = j/T for j = 0, …, N - 1 yields
where the vector f h = (f( - T/2), …, f((N - 1)h - T/2)). Thus, after scaling the
components by
(-1)jh, the discrete
Fourier transform as computed in FFTCF
(with input fh) is related to an
approximation of the continuous Fourier transform by the above formula. This is
seen more clearly by making a change of variables in the last sum. Set
If the function f is expressed as a FORTRAN function routine, then the continuous Fourier transform
can be approximated using the IMSL routine QDAWF (see Chapter 4, Integration and Differentiation).
Inverse Laplace Transform
The last two routines described in this chapter, INLAP and SINLP, compute the inverse Laplace transforms.
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |