Solves an initial-value problem for ordinary differential equations using the Runge-Kutta-Verner fifth-order and sixth-order method.
Required Arguments
IDO — Flag indicating the state of the computation. (Input/Output)
IDO State
1 Initial entry
2 Normal re-entry
3 Final call to release workspace
4 Return because of interrupt 1
5 Return because of interrupt 2 with step accepted
6 Return because of interrupt 2 with step rejected
Normally, the initial call is made with IDO = 1. The routine then sets IDO = 2, and this value is used for all but the last call that is made with IDO = 3. This final call is used to release workspace, which was automatically allocated by the initial call with IDO = 1. No integration is performed on this final call. See Comment 3 for a description of the other interrupts.
FCN —
User-supplied SUBROUTINE to evaluate
functions. The usage is
CALL FCN(N, T, Y, YPRIME),
where
N – Number of
equations.
(Input)
T – Independent
variable, t.
(Input)
Y – Array of
size N
containing the dependent variable values, y.
(Input)
YPRIME – Array
of size N
containing the values of the vector yʹ
evaluated at (t, y). (Output)
FCN must be declared
EXTERNAL in the
calling program.
T — Independent
variable. (Input/Output)
On input, T contains the initial
value. On output, T is replaced by TEND unless error
conditions have occurred. See IDO for details.
TEND — Value of
t where the solution is required. (Input)
The value TEND may be less than
the initial value of t.
Y — Array of size
NEQ of dependent
variables. (Input/Output)
On input, Y contains the initial
values. On output, Y contains the
approximate solution.
Optional Arguments
NEQ — Number of
differential equations. (Input)
Default: NEQ = size (Y,1).
TOL — Tolerance
for error control. (Input)
An attempt is made to control the
norm of the local error such that the global error is proportional to TOL.
Default: TOL = machine
precision.
PARAM — A
floating-point array of size 50 containing optional
parameters. (Input/ Output)
If a parameter is zero, then a
default value is used. These default values are given below. Parameters that
concern values of step size are applied in the direction of integration. The
following parameters may be set by the user:
|
|
PARAM |
Meaning |
|
1 |
HINIT |
Initial value of the step size. Default: 10.0 * MAX (AMACH (1), AMACH(4) * MAX(ABS(TEND), ABS(T))) |
|
2 |
HMIN |
Minimum value of the step size. Default: 0.0 |
|
3 |
HMAX |
Maximum value of the step size. Default: 2.0 |
|
4 |
MXSTEP |
Maximum number of steps allowed. Default: 500 |
|
5 |
MXFCN |
Maximum number of function evaluations allowed. Default: No enforced limit. |
|
6 |
|
Not used. |
|
7 |
INTRP1 |
If nonzero, then return with IDO = 4 before each step. See Comment 3. Default: 0. |
|
8 |
INTRP2 |
If nonzero, then return with IDO = 5 after every successful step and with IDO = 6 after every unsuccessful step. See Comment 3. Default: 0. |
|
9 |
SCALE |
A measure of the scale of the problem, such as an approximation to the average value of a norm of the Jacobian matrix along the solution. Default: 1.0 |
|
10 |
INORM |
Switch determining error
norm. In the following, ei is
the absolute value of an estimate of the error in yi(t). 1 − absolute error = max(ei), i = 1 …, NEQ. 2− max(ei/wi), i = 1 …, NEQ where wi = max(|yi (t)|, FLOOR), and FLOOR is PARAM(11). 3 − Scaled Euclidean norm defined as where wi = max(|yi (t)|, 1.0). Other definitions of YMAX can be specified by the user, as explained in Comment 1. |
|
11 |
FLOOR |
Used in the norm computation associated with parameter INORM. Default: 1.0. |
|
1230 |
|
Not used. |
The following entries in PARAM are set by the program.
|
|
PARAM |
Meaning |
|
31 |
HTRIAL |
Current trial step size. |
|
32 |
HMINC |
Computed minimum step size allowed. |
|
33 |
HMAXC |
Computed maximum step size allowed. |
|
34 |
NSTEP |
Number of steps taken. |
|
35 |
NFCN |
Number of function evaluations used. |
|
3650 |
|
Not used. |
FORTRAN 90 Interface
Generic: CALL IVPRK (IDO, FCN, T, TEND, Y [,…])
Specific: The specific interface names are S_IVPRK and D_IVPRK.
FORTRAN 77 Interface
Single: CALL IVPRK (IDO, NEQ, FCN, T, TEND, TOL, PARAM, Y)
Double: The double precision name is DIVPRK.
Description
Routine IVPRK finds an approximation to the solution of a system of first-order differential equations of the form y0 = f (t, y) with given initial data. The routine attempts to keep the global error proportional to a user-specified tolerance. This routine is efficient for nonstiff systems where the derivative evaluations are not expensive.
The routine IVPRK is based on a code designed by Hull, Enright and Jackson (1976, 1977). It uses Runge-Kutta formulas of order five and six developed by J. H. Verner.
Comments
1. Workspace may be explicitly provided, if desired, by use of I2PRK/DI2PRK. The reference is:
CALL I2PRK (IDO, NEQ, FCN, T, TEND, TOL, PARAM, Y, VNORM, WK)
The additional arguments
are as follows: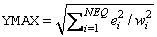
VNORM — A Fortran
SUBROUTINE
to compute the norm of the error. (Input)
The routine may be
provided by the user, or the IMSL routine I3PRK/DI3PRK may be used. In either case, the
name must be declared in a Fortran EXTERNAL statement. If usage of the IMSL
routine is intended, then the name I3PRK/DI3PRK should be used. The usage of the
error norm routine is CALL
VNORM (N, V,
Y, YMAX,
ENORM), where
Arg Definition
N Number of equations. (Input)
V Array of size N containing the vector whose norm is to be computed. (Input)
Y Array of size N containing the values of the dependent variable. (Input)
YMAX Array of size N containing the maximum values of |y(t)|. (Input)
ENORM Norm of the vector V. (Output)
VNORM must be declared EXTERNAL in the calling program.
WK — Work array of size 10N using the working precision. The contents of WK must not be changed from the first call with IDO = 1 until after the final call with IDO = 3.
2. Informational errors
Type Code
4 1 Cannot satisfy error condition. The value of TOL may be too small.
4 2 Too many function evaluations needed.
4 3 Too many steps needed. The problem may be stiff.
3.
If PARAM(7) is
nonzero, the subroutine returns with IDO = 4 and will
resume calculation at the point of interruption if re-entered with IDO = 4. If
PARAM(8) is
nonzero, the subroutine will interrupt the calculations immediately after it
decides whether or not to accept the result of the most recent trial step. The
values used are
IDO = 5 if the routine
plans to accept, or IDO = 6 if it plans to
reject the step. The values of IDO may be changed by
the user (by changing IDO from 6 to 5) in
order to force acceptance of a step that would otherwise be rejected. Some
parameters the user might want to examine after return from an interrupt are
IDO, HTRIAL, NSTEP, NFCN, T, and Y. The array Y contains the newly
computed trial value for y(t), accepted or not.
Example 1
Consider a predator-prey problem with rabbits and foxes.
Let r be the density of rabbits and let
f be the density
of foxes. In the absence of any predator-prey interaction, the rabbits would
increase at a rate proportional to their number, and the foxes would die of
starvation at a rate proportional to their number. Mathematically,
The rate at which the rabbits are eaten by the foxes is 2r f, and the rate at which the foxes increase, because they are eating the rabbits, is r f. So, the model to be solved is
The initial conditions are r(0) = 1 and f(0) = 3 over the interval 0 ≤ t ≤ 10.
In the program Y(1) = r and Y(2) = f. Note that the parameter vector PARAM is first set to zero with IMSL routine SSET (Chapter 9, Basic Matrix/Vector Operations). Then, absolute error control is selected by setting PARAM(10) = 1.0.
The last call to IVPRK with IDO = 3 deallocates IMSL workspace allocated on the first call to IVPRK. It is not necessary to release the workspace in this example because the program ends after solving a single problem. The call to release workspace is made as a model of what would be needed if the program included further calls to IMSL routines.
! SPECIFICATIONS FOR LOCAL VARIABLES
REAL PARAM(MXPARM), T, TEND, TOL, Y(N)
! SPECIFICATIONS FOR SUBROUTINES
! Select absolute error control
CALL IVPRK (IDO, FCN, T, TEND, Y, TOL=TOL, PARAM=PARAM)
WRITE (NOUT,'(I6,3F12.3)') ISTEP, T, Y
! Final call to release workspace
99999 FORMAT (4X, 'ISTEP', 5X, 'Time', 9X, 'Y1', 11X, 'Y2')
SUBROUTINE FCN (N, T, Y, YPRIME)
! SPECIFICATIONS FOR ARGUMENTS
YPRIME(1) = 2.0*Y(1) - 2.0*Y(1)*Y(2)
Output
ISTEP
Time
Y1
Y2
1
1.000
0.078
1.465
2
2.000
0.085
0.578
3
3.000
0.292
0.250
4
4.000
1.449
0.187
5
5.000
4.046
1.444
6
6.000
0.176
2.256
7
7.000 0.066
0.908
8
8.000
0.148
0.367
9
9.000
0.655
0.188
10
10.000
3.157 0.352
Additional Examples
Example 2
This is a mildly stiff problem (F2) from the test set of Enright and Pryce (1987). It is included here because it illustrates the inefficiency of requiring more function evaluations with a nonstiff solver, for a requested accuracy, than would be required using a stiff solver. Also, see IVPAG Example 2, where the problem is solved using a BDF method. The number of function evaluations may vary, depending on the accuracy and other arithmetic characteristics of the computer. The test problem has n = 2 equations:

USE IVPRK_INT
USE UMACH_INT
IMPLICIT NONE
INTEGER MXPARM, N
PARAMETER (MXPARM=50, N=2)
! SPECIFICATIONS FOR LOCAL VARIABLES
INTEGER IDO, ISTEP, NOUT
REAL PARAM(MXPARM), T, TEND, TOL, Y(N)
! SPECIFICATIONS FOR SUBROUTINES
! SPECIFICATIONS FOR FUNCTIONS
EXTERNAL FCN
!
CALL UMACH (2, NOUT)
! Set initial conditions
T = 0.0
Y(1) = 1.0
Y(2) = 0.0
! Set error tolerance
TOL = 0.001
! Set PARAM to default
PARAM = 0.0E0
! Select absolute error control
PARAM(10) = 1.0
! Print header
WRITE (NOUT,99998)
IDO = 1
ISTEP = 0
10 CONTINUE
ISTEP = ISTEP + 24
TEND = ISTEP
CALL IVPRK (IDO, FCN, T, TEND, Y, TOL=TOL, PARAM=PARAM)
IF (ISTEP .LE. 240) THEN
WRITE (NOUT,'(I6,3F12.3)') ISTEP/24, T, Y
! Final call to release workspace
IF (ISTEP .EQ. 240) IDO = 3
GO TO 10
END IF
! Show number of function calls.
WRITE (NOUT,99999) PARAM(35)
99998 FORMAT (4X, 'ISTEP', 5X, 'Time', 9X, 'Y1', 11X, 'Y2')
99999 FORMAT (4X, 'Number of fcn calls with IVPRK =', F6.0)
END
SUBROUTINE FCN (N, T, Y, YPRIME)
! SPECIFICATIONS FOR ARGUMENTS
INTEGER N
REAL T, Y(N), YPRIME(N)
! SPECIFICATIONS FOR DATA VARIABLES
REAL AK1, AK2, AK3
!
DATA AK1, AK2, AK3/294.0E0, 3.0E0, 0.01020408E0/
!
YPRIME(1) = -Y(1) - Y(1)*Y(2) + AK1*Y(2)
YPRIME(2) = -AK2*Y(2) + AK3*(1.0E0-Y(2))*Y(1)
RETURN
END
Output
ISTEP
Time
Y1
Y2
1
24.000
0.688
0.002
2
48.000
0.634
0.002
3 72.000
0.589
0.002
4
96.000
0.549
0.002
5
120.000
0.514
0.002
6
144.000
0.484
0.002
7
168.000
0.457
0.002
8
192.000
0.433
0.001
9
216.000
0.411 0.001
10
240.000
0.391 0.001
Number of fcn calls with
IVPRK = 2153.
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |