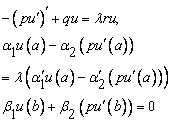A differential equation is an equation involving one or more dependent variables (called yi or ui), their derivatives, and one or more independent variables (called t, x, and y). Users will typically need to relabel their own model variables so that they correspond to the variables used in the solvers described here. A differential equation with one independent variable is called an ordinary differential equation (ODE). A system of equations involving derivatives in one independent variable and other dependent variables is called a differential-algebraic system. A differential equation with more than one independent variable is called a partial differential equation (PDE). The order of a differential equation is the highest order of any of the derivatives in the equation. Some of the routines in this chapter require the user to reduce higher-order problems to systems of first-order differential equations.

Ordinary Differential Equations

It is convenient to use the vector notation below. We denote the number of equations as the value N. The problem statement is abbreviated by writing it as a system of first-order ODEs

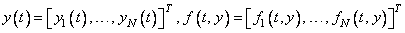
The problem becomes

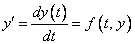
with initial values y (t0). Values of y(t) for t > t0 or t < t0are required. The routines IVPRK, IVMRK, and IVPAG, solve the IVP for systems of ODEs of the form yʹ = f (t, y) with y(t = t0) specified. Here, f is a user supplied function that must be evaluated at any set of values (t, y1, …, yN);
i = 1, …, N. The routines IVPAG, and DASPG, will also solve implicit systems of the form Ayʹ = f (t, y) where A is a user supplied matrix. For IVPAG, the matrix A must be nonsingular.

The system yʹ = f (t, y) is said to be stiff if some of the eigenvalues of the Jacobian matrix
{ fi yj} have large, negative real parts. This is often the case for differential equations representing the behavior of physical systems such as chemical reactions proceeding to equilibrium where subspecies effectively complete their reaction in different epochs. An alternate model concerns discharging capacitors such that different parts of the system have widely varying decay rates (or time constants). This definition of stiffness, based on the eigenvalues of the Jacobian matrix, is not satisfactory. Users typically identify stiff systems by the fact that numerical differential equation solvers such as IVPRK, are inefficient, or else they fail. The most common inefficiency is that a large number of evaluations of the functions fi are required. In such cases, use routine IVPAG, or DASPG. For more about stiff systems, see Gear (1971, Chapter 11) or Shampine and Gear (1979).

In the boundary value problem (BVP) for ODEs, constraints on the dependent variables are given at the endpoints of the interval of interest, [a, b]. The routines BVPFD and BVPMS solve the BVP for systems of the form yʹ (t) = f (t, y), subject to the conditions

hi(y1(a), …, yN(a), y1 (b), …, yN(b)) = 0   i = 1, …, N

Here, f and h = [h1 , …, hN]T are user-supplied functions.

Differential-algebraic Equations

Frequently, it is not possible or not convenient to express the model of a dynamical system as a set of ODEs. Rather, an implicit equation is available in the form

The gi are user-supplied functions. The system is abbreviated as

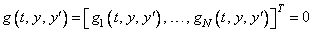
With initial value y(t0). Any system of ODEs can be trivially written as a differential-algebraic system by defining

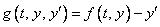
The routine DASPG solves differential-algebraic systems of index 1 or index 0. For a definition of index of a differential-algebraic system, see (Brenan et al. 1989). Also, see Gear and Petzold (1984) for an outline of the computing methods used.

Partial Differential Equations

The routine MOLCH solves the IVP problem for systems of the form

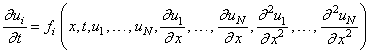
subject to the boundary conditions

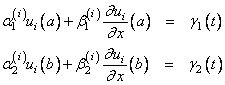
and subject to the initial conditions

ui(x, t = t0) = gi(x)

for i = 1, , N. Here, fi, gi,

are user-supplied, j = 1, 2.

The routines FPS2H and FPS3H solve Laplace's, Poisson's, or Helmholtz's equation in two or three dimensions. FPS2H uses a fast Poisson method to solve a PDE of the form

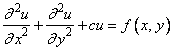
over a rectangle, subject to boundary conditions on each of the four sides. The scalar constant c and the function f are user specified. FPS3H solves the three-dimensional analogue of this problem.

Users wishing to solve more general PDE's, in more general 2-d and 3-d regions are referred to Visual Numerics' partner PDE2D (www.pde2d.com).

Summary

The following table summarizes the types of problems handled by the routines in this chapter. With the exception of FPS2H and FPS3H, the routines can handle more than one differential equation.

 

Problem	Consideration	Routine
Ayʹ= f(t, y) y(t0) = y0	A is a general, symmetric positive definite, band or symmetric positive definite band matrix.	IVPAG
	Stiff or expensive to evaluate f (t, y), banded Jacobian or finely spaced output needed.	IVPAG
yʹ = f(t, y), y (t0) = y0	High accuracy needed and not stiff. (Uses Adams methods)	IVPAG
	Moderate accuracy needed and not stiff.	IVPRK
yʹ = f(t, y) h(y(a), y(b)) = 0	BVP solver using finite differences	BVPFD
	BVP solver using multiple shooting	BVPMS
g(t, y, yʹ) = 0 y(t0), yʹ(t0) given	Stiff, differential-algebraic solver for systems of index 1 or 0. Note: DASPG uses the user-supplied yʹ(t0) only as an initial guess to help it find the correct initial yʹ( t0) to get started.	DASPG
ut = f(x, t, u, ux, uxx) α1u(a) + β1 ux(a) = γ1 (t) α2 u(b) + β2 ux(b) = γ2(t)	Method of lines using cubic splines and ODEs.	MOLCH
uxx + uyy + cu = f(x, y) on a rectangle, given u or un on each edge.	Fast Poisson solver	FPS2H
uxx + uyy + uzz + cu = f(x, y, z) on a box, given u or un on each face	Fast Poisson solver	FPS3H
	Sturm-Liouville problems	SLEIG

Visual Numerics, Inc. Visual Numerics - Developers of IMSL and PV-WAVE http://www.vni.com/ PHONE: 713.784.3131 FAX:713.781.9260