LIN_EIG_SELF.p>.F90CH2.DOC!LIN_EIG_SELF;
Computes the eigenvalues of a self-adjoint (i.e. real symmetric or complex Hermitian) matrix, A. Optionally, the eigenvectors can be computed. This gives the decomposition A = VDVT , where V is an n × n orthogonal matrix and D is a real diagonal matrix.
Required Arguments
A — Array of size n × n containing the matrix. (Input [/Output])
D — Array of size n containing the eigenvalues. The values are in order of decreasing absolute value. (Output)
Optional Arguments
NROWS = n
(Input)
Uses array A(1:n, 1:n) for the input
matrix.
Default: n = size(A, 1)
v = v(:,:)
(Output)
Array of the same type and kind as A(1:n, 1:n). It contains the
n × n orthogonal matrix V.
iopt =
iopt(:) (Input)
Derived type array with the same precision
as the input matrix; used for passing optional data to the routine. The options
are as follows:
|
Packaged Options for LIN_EIG_SELF | ||
|
Option Prefix = ? |
Option Name |
Option Value |
|
s_, d_, c_, z_ |
Lin_eig_self_set_small |
1 |
|
s_, d_, c_, z_ |
Lin_eig_self_overwrite_input |
2 |
|
s_, d_, c_, z_ |
Lin_eig_self_scan_for_NaN |
3 |
|
s_, d_, c_, z_ |
Lin_eig_self_use_QR |
4 |
|
s_, d_, c_, z_ |
Lin_eig_self_skip_Orth |
5 |
|
s_, d_, c_, z_ |
Lin_eig_self_use_Gauss_elim |
6 |
|
s_, d_, c_, z_ |
Lin_eig_self_set_perf_ratio |
7 |
iopt(IO) =
?_options(?_lin_eig_self_set_small, Small)
If a denominator
term is smaller in magnitude than the value Small, it is replaced by
Small.
Default: the smallest number that can be reciprocated
safely
iopt(IO) =
?_options(?_lin_eig_self_overwrite_input, ?_dummy)
Do not save the
input array A(:, :).
iopt(IO) =
?_options(?_lin_eig_self_scan_for_NaN, ?_dummy)
Examines each input
array entry to find the first value such that
isNaN(a(i,j)) == .true.
See the isNaN() function, Chapter 10.
Default: The
array is not scanned for NaNs.
iopt(IO) =
?_options(?_lin_eig_use_QR, ?_dummy)
Uses a rational QR
algorithm to compute eigenvalues. Accumulate the eigenvectors using this
algorithm.
Default: the eigenvectors computed using inverse iteration
iopt(IO) =
?_options(?_lin_eig_skip_Orth, ?_dummy)
If the eigenvalues are
computed using inverse iteration, skips the final orthogonalization of the
vectors. This will result in a more efficient computation but the eigenvectors,
while a complete set, may be far from orthogonal.
Default: the eigenvectors
are normally orthogonalized if obtained using inverse iteration.
iopt(IO) =
?_options(?_lin_eig_use_Gauss_elim, ?_dummy)
If the eigenvalues are
computed using inverse iteration, uses standard elimination with partial
pivoting to solve the inverse iteration problems.
Default: the eigenvectors
computed using cyclic reduction
iopt(IO) =
?_options(?_lin_eig_self_set_perf_ratio, perf_ratio)
Uses residuals
for approximate normalized eigenvectors if they have a performance index no
larger than perf_ratio. Otherwise an alternate approach is taken and the
eigenvectors are computed again: Standard elimination is used instead of cyclic
reduction, or the standard QR algorithm is used as a backup procedure to
inverse iteration. Larger values of perf_ratio are less likely to cause
these exceptions.
Default: perf_ratio = 4
FORTRAN 90 Interface
Generic: CALL LIN_EIG_SELF (A, D [,…])
Specific: The specific interface names are S_LIN_EIG_SELF, D_LIN_EIG_SELF, C_LIN_EIG_SELF, and Z_LIN_EIG_SELF.
Description
Routine LIN_EIG_SELF is an implementation of the QR algorithm for self-adjoint matrices. An orthogonal similarity reduction of the input matrix to self-adjoint tridiagonal form is performed. Then, the eigenvalue-eigenvector decomposition of a real tridiagonal matrix is calculated. The expansion of the matrix as AV = VD results from a product of these matrix factors. See Golub and Van Loan (1989, Chapter 8) for details.
Fatal, Terminal, and Warning Error Messages
See the messages.gls file for error messages for LIN_EIG_SELF. These error messages are numbered 81-90; 101-110; 121-129; 141-149.
.p>.F90CH2.DOC!EX1_LIN_EIG_SELF;Example 1: Computing Eigenvalues
The eigenvalues of a self-adjoint matrix are computed. The matrix A = C+CT is used, where C is random. The magnitudes of eigenvalues of A agree with the singular values of A. Also, see operator_ex25, supplied with the product examples.
use lin_eig_self_int
use lin_sol_svd_int
use rand_gen_int
implicit none
! This is Example 1 for LIN_EIG_SELF.
integer, parameter :: n=64
real(kind(1e0)), parameter :: one=1e0
real(kind(1e0)) :: A(n,n), b(n,0), D(n), S(n), x(n,0), y(n*n)
! Generate a random matrix and from it
! a self-adjoint matrix.
call rand_gen(y)
A = reshape(y,(/n,n/))
A = A + transpose(A)
! Compute the eigenvalues of the matrix.
call lin_eig_self(A, D)
! For comparison, compute the singular values.
call lin_sol_svd(A, b, x, nrhs=0, s=S)
! Check the results: Magnitude of eigenvalues should equal
! the singular values.
if (sum(abs(abs(D) - S)) <= &
sqrt(epsilon(one))*S(1)) then
write (*,*) 'Example 1 for LIN_EIG_SELF is correct.'
end if
end
Output
Example 1 for LIN_EIG_SELF is correct.
Additional Examples
.p>.F90CH2.DOC!EX2_LIN_EIG_SELF;Example 2: Eigenvalue-Eigenvector Expansion of a Square Matrix
A self-adjoint matrix is generated and the eigenvalues and
eigenvectors are computed. Thus,
A = VDVT, where V is
orthogonal and D is a real diagonal matrix. The matrix V is
obtained using an optional argument. Also, see operator_ex26,
Chapter 10.
use lin_eig_self_int
use rand_gen_int
implicit none
! This is Example 2 for LIN_EIG_SELF.
integer, parameter :: n=8
real(kind(1e0)), parameter :: one=1e0
real(kind(1e0)) :: a(n,n), d(n), v_s(n,n), y(n*n)
! Generate a random self-adjoint matrix.
call rand_gen(y)
a = reshape(y,(/n,n/))
a = a + transpose(a)
! Compute the eigenvalues and eigenvectors.
call lin_eig_self(a, d, v=v_s)
! Check the results for small residuals.
if (sum(abs(matmul(a,v_s)-v_s*spread(d,1,n)))/d(1) <= &
sqrt(epsilon(one))) then
write (*,*) 'Example 2 for LIN_EIG_SELF is correct.'
end if
end
Output
Example 2 for LIN_EIG_SELF is correct.
.p>.F90CH2.DOC!EX3_LIN_EIG_SELF;.p>.F90CH2.DOC!EX3_LIN_EIG_SELF;Example 3: Computing a few Eigenvectors with Inverse Iteration
A self-adjoint n × n matrix is generated and
the eigenvalues, 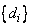 , are
computed. The eigenvectors associated with the first k of these are
computed using the self-adjoint solver, lin_sol_self,
and inverse iteration. With random right-hand sides, these systems are as
follows:
, are
computed. The eigenvectors associated with the first k of these are
computed using the self-adjoint solver, lin_sol_self,
and inverse iteration. With random right-hand sides, these systems are as
follows:
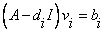
The solutions are then
orthogonalized as in Hanson et al. (1991) to comprise a partial decomposition
AV = VD where V is an n × k matrix
resulting from the orthogonalized 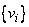 and D is the k × k diagonal
matrix of the distinguished eigenvalues. It is necessary to suppress the error
message when the matrix is singular. Since these singularities are desirable, it
is appropriate to ignore the exceptions and not print the message text. Also,
see
operator_ex27, supplied with the product examples.
and D is the k × k diagonal
matrix of the distinguished eigenvalues. It is necessary to suppress the error
message when the matrix is singular. Since these singularities are desirable, it
is appropriate to ignore the exceptions and not print the message text. Also,
see
operator_ex27, supplied with the product examples.
use lin_eig_self_int
use lin_sol_self_int
use rand_gen_int
use error_option_packet
implicit none
! This is Example 3 for LIN_EIG_SELF.
integer i, j
integer, parameter :: n=64, k=8
real(kind(1d0)), parameter :: one=1d0, zero=0d0
real(kind(1d0)) big, err
real(kind(1d0)) :: a(n,n), b(n,1), d(n), res(n,k), temp(n,n), &
v(n,k), y(n*n)
type(d_options) :: iopti(2)=d_options(0,zero)
! Generate a random self-adjoint matrix.
call rand_gen(y)
a = reshape(y,(/n,n/))
a = a + transpose(a)
! Compute just the eigenvalues.
call lin_eig_self(a, d)
do i=1, k
! Define a temporary array to hold the matrices A - eigenvalue*I.
temp = a
do j=1, n
temp(j,j) = temp(j,j) - d(i)
end do
! Use packaged option to reset the value of a small diagonal.
iopti(1) = d_options(d_lin_sol_self_set_small,&
epsilon(one)*abs(d(i)))
! Use packaged option to skip singularity messages.
iopti(2) = d_options(d_lin_sol_self_no_sing_mess,&
zero)
call rand_gen(b(1:n,1))
call lin_sol_self(temp, b, v(1:,i:i),&
iopt=iopti)
end do
! Orthogonalize the eigenvectors.
do i=1, k
big = maxval(abs(v(1:,i)))
v(1:,i) = v(1:,i)/big
v(1:,i) = v(1:,i)/sqrt(sum(v(1:,i)**2))
if (i == k) cycle
v(1:,i+1:k) = v(1:,i+1:k) + &
spread(-matmul(v(1:,i),v(1:,i+1:k)),1,n)* &
spread(v(1:,i),2,k-i)
end do
do i=k-1, 1, -1
v(1:,i+1:k) = v(1:,i+1:k) + &
spread(-matmul(v(1:,i),v(1:,i+1:k)),1,n)* &
spread(v(1:,i),2,k-i)
end do
! Check the results for both orthogonality of vectors and small
! residuals.
res(1:k,1:k) = matmul(transpose(v),v)
do i=1,k
res(i,i)=res(i,i)-one
end do
err = sum(abs(res))/k**2
res = matmul(a,v) - v*spread(d(1:k),1,n)
if (err <= sqrt(epsilon(one))) then
if (sum(abs(res))/abs(d(1)) <= sqrt(epsilon(one))) then
write (*,*) 'Example 3 for LIN_EIG_SELF is correct.'
end if
end if
end
Output
Example 3 for LIN_EIG_SELF is correct.
.p>.F90CH2.DOC!EX4_LIN_EIG_SELF;Example 4: Analysis and Reduction of a Generalized Eigensystem
A generalized eigenvalue problem is Ax = lBx, where A and B are n × n self-adjoint matrices. The matrix B is positive definite. This problem is reduced to an ordinary self-adjoint eigenvalue problem Cy = ly by changing the variables of the generalized problem to an equivalent form. The eigenvalue-eigenvector decomposition B = VSVT is first computed, labeling an eigenvalue too small if it is less than epsilon(1.d0). The ordinary self-adjoint eigenvalue problem is Cy = ly provided that the rank of B, based on this definition of Small, has the value n. In that case,
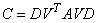
where
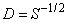
The relationship between x and y is
summarized as X = VDY, computed after the ordinary eigenvalue
problem is solved for the eigenvectors Y of C. The matrix X
is normalized so that each column has Euclidean length of value one. This
solution method is nonstandard for any but the most
ill-conditioned matrices
B. The standard approach is to compute an ordinary self-adjoint problem
following computation of the Cholesky decomposition
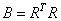
where R is upper triangular. The computation of C can also be completed efficiently by exploiting its self-adjoint property. See Golub and Van Loan (1989, Chapter 8) for more information. Also, see operator_ex28, Chapter 10.
use lin_eig_self_int
use rand_gen_int
implicit none
! This is Example 4 for LIN_EIG_SELF.
integer i
integer, parameter :: n=64
real(kind(1e0)), parameter :: one=1d0
real(kind(1e0)) b_sum
real(kind(1e0)), dimension(n,n) :: A, B, C, D(n), lambda(n), &
S(n), vb_d, X, ytemp(n*n), res
! Generate random self-adjoint matrices.
call rand_gen(ytemp)
A = reshape(ytemp,(/n,n/))
A = A + transpose(A)
call rand_gen(ytemp)
B = reshape(ytemp,(/n,n/))
B = B + transpose(B)
b_sum = sqrt(sum(abs(B**2))/n)
! Add a scalar matrix so B is positive definite.
do i=1, n
B(i,i) = B(i,i) + b_sum
end do
! Get the eigenvalues and eigenvectors for B.
call lin_eig_self(B, S, v=vb_d)
! For full rank problems, convert to an ordinary self-adjoint
! problem. (All of these examples are full rank.)
if (S(n) > epsilon(one)) then
D = one/sqrt(S)
C = spread(D,2,n)*matmul(transpose(vb_d), &
matmul(A,vb_d))*spread(D,1,n)
! Get the eigenvalues and eigenvectors for C.
call lin_eig_self(C, lambda, v=X)
! Compute the generalized eigenvectors.
X = matmul(vb_d,spread(D,2,n)*X)
! Normalize the eigenvectors for the generalized problem.
X = X * spread(one/sqrt(sum(X**2,dim=2)),1,n)
res = matmul(A,X) - &
matmul(B,X)*spread(lambda,1,n)
! Check the results.
if (sum(abs(res))/(sum(abs(A))+sum(abs(B))) <= &
sqrt(epsilon(one))) then
write (*,*) 'Example 4 for LIN_EIG_SELF is correct.'
end if
end if
end
Output
Example 4 for LIN_EIG_SELF is correct.
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |