This chapter includes routines for linear eigensystem analysis. Many of these are for matrices with special properties. Some routines compute just a portion of the eigensystem. Use of the appropriate routine can substantially reduce computing time and storage requirements compared to computing a full eigensystem for a general complex matrix.
An ordinary linear eigensystem problem is represented by
the equation Ax = lx
where A denotes an
n × n matrix. The value l is an eigenvalue and x ≠ 0 is
the corresponding eigenvector. The eigenvector is determined up to a
scalar factor. In all routines, we have chosen this factor so that x has
Euclidean length with value one, and the component of x of smallest index
and largest magnitude is positive. In case x is a complex vector, this
largest component is real and positive.
Similar comments hold for the use of the remaining Level 1 routines in the following tables in those cases where the second character of the Level 2 routine name is no longer the character "2".
A generalized linear eigensystem problem is represented by Ax = lBx where A and B are n × n matrices. The value l is an eigenvalue, and x is the corresponding eigenvector. The eigenvectors are normalized in the same manner as for the ordinary eigensystem problem. The linear eigensystem routines have names that begin with the letter “E”. The generalized linear eigensystem routines have names that begin with the letter “G”. This prefix is followed by a two-letter code for the type of analysis that is performed. That is followed by another two-letter suffix for the form of the coefficient matrix. The following tables summarize the names of the eigensystem routines.
|
Symmetric and Hermitian Eigensystems | |||
|
|
Symmetric |
Symmetric |
Hermitian |
|
All eigenvalues |
|||
|
All eigenvalues |
|||
|
Extreme eigenvalues |
|||
|
Extreme eigenvalues |
|||
|
Eigenvalues in |
|||
|
Eigenvalues and |
|||
|
Performance index |
|||
|
General Eigensystems | ||||
|
|
Real |
Complex |
Real |
Complex |
|
All eigenvalues |
||||
|
All eigenvalues and eigenvectors |
||||
|
Performance index |
||||
|
Generalized Eigensystems Ax = lBx | |||
|
|
Real |
Complex |
A Symmetric |
|
All eigenvalues |
|||
|
All eigenvalues and eigenvectors |
|||
|
Performance index |
|||
Error Analysis and Accuracy
The remarks in this section are for the ordinary eigenvalue problem. Except in special cases, routines will not return the exact eigenvalue-eigenvector pair for the ordinary eigenvalue problem Ax = lx. The computed pair
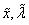
is an exact eigenvector-eigenvalue pair for a “nearby” matrix A + E. Information about E is known only in terms of bounds of the form || E||2 ≤ ¦(n) ||A||2 ε. The value of ¦(n) depends on the algorithm but is typically a small fractional power of n. The parameter ε is the machine precision. By a theorem due to Bauer and Fike (see Golub and Van Loan [1989, page 342],
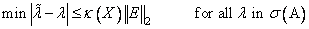
where σ (A) is the set of all eigenvalues of
A (called the spectrum of A), X is the matrix of
eigenvectors, || × ||2 is the 2-norm, and
κ(X) is the condition number of X defined as
κ (X) = ||
X ||2 || X-1 ||2. If A is a real symmetric or
complex Hermitian matrix, then its eigenvector matrix X is respectively
orthogonal or unitary. For these matrices, κ(X) = 1.
The eigenvalues
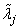
and eigenvectors
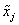
computed by EVC** can be checked by computing their performance index τ using EPI**. The performance index is defined by Smith et al. (1976, pages 124− 126) to be
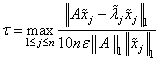
No significance should be attached to the factor of 10 used in the denominator. For a real vector x, the symbol || x ||1 represents the usual 1-norm of x. For a complex vector x, the symbol || x ||1 is defined by

The performance index τ is related to the error analysis because
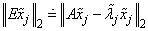
where E is the “nearby” matrix discussed above.
While the exact value of τ is machine and precision dependent, the performance of an eigensystem analysis routine is defined as excellent if τ < 1, good if 1 ≤ τ ≤ 100, and poor if τ > 100. This is an arbitrary definition, but large values of τ can serve as a warning that there is a blunder in the calculation. There are also similar routines GPI** to compute the performance index for generalized eigenvalue problems.
If the condition number κ(X) of the eigenvector matrix X is large, there can be large errors in the eigenvalues even if τ is small. In particular, it is often difficult to recognize near multiple eigenvalues or unstable mathematical problems from numerical results. This facet of the eigenvalue problem is difficult to understand: A user often asks for the accuracy of an individual eigenvalue. This can be answered approximately by computing the condition number of an individual eigenvalue. See Golub and Van Loan (1989, pages 344-345). For matrices A such that the computed array of normalized eigenvectors X is invertible, the condition number of lj is κj º the Euclidean length of row j of the inverse matrix X-1. Users can choose to compute this matrix with routine LINCG, see Chapter 1, Linear Systems. An approximate bound for the accuracy of a computed eigenvalue is then given by κj ε|| A ||. To compute an approximate bound for the relative accuracy of an eigenvalue, divide this bound by | lj |.
Reformulating Generalized Eigenvalue Problems
The generalized eigenvalue problem Ax = lBx is often difficult for users to
analyze because it is frequently ill-conditioned. There are occasionally changes
of variables that can be performed on the given problem to ease this
ill-conditioning. Suppose that B is singular but A is nonsingular.
Define the reciprocal μ = l-1. Then, the roles of
A and B are interchanged so that the reformulated problem
Bx = μAx is solved. Those generalized eigenvalues μj = 0 correspond to
eigenvalues lj = ∞. The remaining
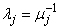
The generalized eigenvectors for lj correspond to those for μj. Other reformulations can be made: If B is nonsingular, the user can solve the ordinary eigenvalue problem Cx º B-1 Ax = lx. This is not recommended as a computational algorithm for two reasons. First, it is generally less efficient than solving the generalized problem directly. Second, the matrix C will be subject to perturbations due to ill-conditioning and rounding errors when computing B-1 A. Computing the condition numbers of the eigenvalues for C may, however, be helpful for analyzing the accuracy of results for the generalized problem.
There is another method that users can consider to reduce the generalized problem to an alternate ordinary problem. This technique is based on first computing a matrix decomposition B = PQ, where both P and Q are matrices that are “simple” to invert. Then, the given generalized problem is equivalent to the ordinary eigenvalue problem Fy = ly. The matrix F º P-1 AQ-1. The unnormalized eigenvectors of the generalized problem are given by x = Q-1 y. An example of this reformulation is used in the case where A and B are real and symmetric with B positive definite. The IMSL routines GVLSP and GVCSP use P = RT and Q = R where R is an upper triangular matrix obtained from a Cholesky decomposition, B = RTR. The matrix F = R-T AR-1 is symmetric and real. Computation of the eigenvalue-eigenvector expansion for F is based on routine EVCSF.
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |