Computes the QR decomposition, AP = QR, using Householder transformations.

Required Arguments

A — Real NRA by NCA matrix containing the matrix whose QR factorization is to be computed.   (Input)

QR — Real NRA by NCA matrix containing information required for the QR factorization.   (Output)
The upper trapezoidal part of QR contains the upper trapezoidal part of R with its diagonal elements ordered in decreasing magnitude. The strict lower trapezoidal part of QR contains information to recover the orthogonal matrix Q of the factorization. Arguments A and QR can occupy the same storage locations. In this case, A will not be preserved on output.

QRAUX — Real vector of length NCA containing information about the orthogonal part of the decomposition in the first min(NRA, NCA) position. (Output)

Optional Arguments

NRA — Number of rows of A.   (Input)
Default: NRA = size (A,1).

NCA — Number of columns of A.   (Input)
Default: NCA = size (A,2).

LDA — Leading dimension of A exactly as specified in the dimension statement of the calling program.   (Input)
Default: LDA = size (A,1).

PIVOT — Logical variable.   (Input)
PIVOT = .TRUE. means column pivoting is enforced.
PIVOT = .FALSE. means column pivoting is not done.
Default: PIVOT = .TRUE.

IPVT — Integer vector of length NCA containing information that controls the final order of the columns of the factored matrix A.   (Input/Output)
On input, if IPVT(K) > 0, then the K-th column of A is an initial column. If IPVT(K) = 0, then the K-th column of A is a free column. If IPVT(K) < 0, then the K-th column of A is a final column. See Comments.
On output, IPVT(K) contains the index of the column of A that has been interchanged into the K-th column. This defines the permutation matrix P. The array IPVT is referenced only if PIVOT is equal to .TRUE.
Default: IPVT = 0.

LDQR — Leading dimension of QR exactly as specified in the dimension statement of the calling program.   (Input)
Default: LDQR = size (QR,1).

CONORM — Real vector of length NCA containing the norms of the columns of the input matrix.   (Output)
If this information is not needed, CONORM and QRAUX can share the same storage locations.

FORTRAN 90 Interface

Generic:                              CALL LQRRR (A, QR, QRAUX [,…])

Specific:                             The specific interface names are S_LQRRR and D_LQRRR.

FORTRAN 77 Interface

Single:            CALL LQRRR (NRA, NCA, A, LDA, PIVOT, IPVT, QR, LDQR, QRAUX, CONORM)

Double:                              The double precision name is DLQRRR.

ScaLAPACK Interface

Generic:                              CALL LQRRR (A0, QR0, QRAUX0 [,…])

Specific:                             The specific interface names are S_LQRRR and D_LQRRR.

See the ScaLAPACK Usage Notes below for a description of the arguments for distributed computing.

Description

The routine LQRRR computes the QR decomposition of a matrix using Householder transformations. The underlying code is based on either LINPACK , LAPACK, or ScaLAPACK code depending upon which supporting libraries are used during linking. For a detailed explanation see “Using ScaLAPACK, LAPACK, LINPACK, and EISPACK” in the Introduction section of this manual.

LQRRR determines an orthogonal matrix Q, a permutation matrix P, and an upper trapezoidal matrix R with diagonal elements of nonincreasing magnitude, such that AP = QR. The Householder transformation for column k is of the form

for k = 1, 2, …, min(NRA, NCA), where u has zeros in the first k − 1 positions. The matrix Q is not produced directly by LQRRR . Instead the information needed to reconstruct the Householder transformations is saved. If the matrix Q is needed explicitly, the subroutine LQERR can be called after LQRRR. This routine accumulates Q from its factored form.

Before the decomposition is computed, initial columns are moved to the beginning of the array A and the final columns to the end. Both initial and final columns are frozen in place during the computation. Only free columns are pivoted. Pivoting, when requested, is done on the free columns of largest reduced norm.

Comments

1.         Workspace may be explicitly provided, if desired, by use of L2RRR/DL2RRR. The reference is:

CALL L2RRR (NRA, NCA, A, LDA, PIVOT, IPVT, QR, LDQR, QRAUX, CONORM,
 WORK)

The additional argument is

WORK — Work vector of length 2NCA − 1. Only NCA − 1 locations of WORK are referenced if PIVOT = .FALSE. .

2.         LQRRR determines an orthogonal matrix Q, permutation matrix P, and an upper trapezoidal matrix R with diagonal elements of nonincreasing magnitude, such that
AP = QR. The Householder transformation for column k, k = 1, …, min(NRA, NCA) is of the form

where u has zeros in the first k − 1 positions. If the explicit matrix Q is needed, the user can call routine LQERR after calling LQRRR. This routine accumulates Q from its factored form.

3.         Before the decomposition is computed, initial columns are moved to the beginning and the final columns to the end of the array A. Both initial and final columns are not moved during the computation. Only free columns are moved. Pivoting, if requested, is done on the free columns of largest reduced norm.

4.         When pivoting has been selected by having entries of IPVT initialized to zero, an estimate of the condition number of A can be obtained from the output by computing the magnitude of the number QR(1, 1)/QR(K, K), where K = MIN(NRA, NCA). This estimate can be used to select the number of columns, KBASIS, used in the solution step computed with routine LQRSL.

ScaLAPACK Usage Notes

The arguments which differ from the standard version of this routine are:

A0 —   MXLDA by MXCOL local matrix containing the local portions of the distributed matrix A.  A contains the matrix whose QR factorization is to be computed.   (Input)

QR0 —   MXLDA by MXCOL local matrix containing the local portions of the distributed    matrix  QR.  QR contains the information required for the QR factorization.   (Output)
The upper trapezoidal part of QR contains the upper trapezoidal part of R with its diagonal elements ordered in decreasing magnitude. The strict lower trapezoidal part of QR contains information to recover the orthogonal matrix Q of the factorization. Arguments A and QR can occupy the same storage locations. In this case, A will not be preserved on output.

QRAUX0 —   Real vector of length MXCOL containing the local portions of the distributed  matrix  QRAUX.  QRAUX contains information about the orthogonal part of the decomposition in the first MIN(NRA, NCA) position. (Output)

IPVT0 —   Integer vector of length MXLDB containing the local portions of the distributed vector  IPVT.  IPVT contains the information that controls the final order of the columns of the factored matrix A.   (Input/Output)
On input, if IPVT(K) > 0, then the K-th column of A is an initial column. If IPVT(K) = 0, then the K-th column of A is a free column. If IPVT(K) < 0, then the K-th column of A is a final column. See Comments.
On output, IPVT(K) contains the index of the column of A that has been interchanged into the K-th column. This defines the permutation matrix P. The array IPVT is referenced only if PIVOT is equal to .TRUE.
Default: IPVT = 0.

All other arguments are global and are the same as described for the standard version of the routine. In the argument descriptions above, MXLDA, MXLDB, and MXCOL can be obtained through a call to SCALAPACK_GETDIM (see Utilities) after a call to  SCALAPACK_SETUP (see Utilities) has been made. See the ScaLAPACK Example below.

Example

In various statistical algorithms it is necessary to compute q = xT(AT A) -1x, where A is a rectangular matrix of full column rank. By using the QR decomposition, q can be computed without forming ATA. Note that

AT A = (QRP-1)T (QRP-1) = P-T RT (QT Q)RP-1 = P RT RPT

since Q is orthogonal (QTQ = I) and P is a permutation matrix. Let

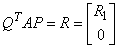
where R1 is an upper triangular nonsingular matrix. Then

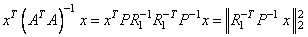
In the following program, first the vector t = P-1 x is computed. Then

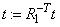
Finally,

 

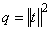
      USE IMSL_LIBRARIES
!                                 Declare variables

      INTEGER    LDA, LDQR, NCA, NRA

      PARAMETER  (NCA=3, NRA=4, LDA=NRA, LDQR=NRA)

!                                 SPECIFICATIONS FOR PARAMETERS

      INTEGER    LDQ

      PARAMETER  (LDQ=NRA)

!                                 SPECIFICATIONS FOR LOCAL VARIABLES

      INTEGER    IPVT(NCA), NOUT

      REAL       CONORM(NCA), Q, QR(LDQR,NCA), QRAUX(NCA), T(NCA)

      LOGICAL    PIVOT

      REAL       A(LDA,NCA), X(NCA)

!
!                                 Set values for A

!

!                                 A = (  1    2     4   )

!                                     (  1    4    16   )

!                                     (  1    6    36   )

!                                     (  1    8    64   )

!

      DATA A/4*1.0, 2.0, 4.0, 6.0, 8.0, 4.0, 16.0, 36.0, 64.0/

!

!                                 Set values for X

!

!                                 X = (  1    2     3  )

      DATA X/1.0, 2.0, 3.0/

!

!                                 QR factorization

      PIVOT = .TRUE.

      IPVT=0

      CALL LQRRR (A, QR, QRAUX, pivot=pivot, IPVT=IPVT)

!                                 Set t = inv(P)*x

      CALL PERMU (X, IPVT, T, IPATH=1)

!                                 Compute t = inv(trans(R))*t

      CALL LSLRT (QR, T, T, IPATH=4)

!                                 Compute 2-norm of t, squared.

      Q = SDOT(NCA,T,1,T,1)

!                                 Print result

      CALL UMACH (2, NOUT)

      WRITE (NOUT,*) 'Q = ', Q

!

      END

Output

 

Q =    0.840624

ScaLAPACK Example

The previous example is repeated here as a distributed computing example. In various statistical algorithms it is necessary to compute q = xT(AT A) -1x, where A is a rectangular matrix of full column rank. By using the QR decomposition, q can be computed without forming AT A. Note that

AT A = (QRP-1)T (QRP-1) = P-T RT (QT Q)RP-1 = P RT RPT

since Q is orthogonal (QTQ = I) and P is a permutation matrix. Let

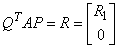
where R1 is an upper triangular nonsingular matrix. Then

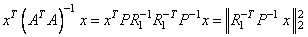
In the following program, first the vector t = P-1 x is computed. Then

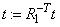
Finally,

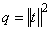
SCALAPACK_MAP and SCALAPACK_UNMAP are IMSL utility routines (see Utilities) used to map and unmap arrays to and from the processor grid. They are used here for brevity. DESCINIT is a ScaLAPACK tools routine which initializes the descriptors for the local arrays.

 

      USE MPI_SETUP_INT
      USE LQRRR_INT
      USE PERMU_INT
      USE LSLRT_INT
      USE UMACH_INT
      USE SCALAPACK_SUPPORT
      IMPLICIT NONE
      INCLUDE ‘mpif.h'

!                                 Declare variables

      INTEGER        LDA, LDQR, NCA, NRA, DESCA(9), DESCB(9), DESCL(9)
      INTEGER       INFO, MXCOL, MXLDA, MXLDB, MXCOLB, NOUT
      INTEGER, ALLOCATABLE ::     IPVT(:), IPVT0(:)
      LOGICAL       PIVOT

      REAL          Q
      REAL, ALLOCATABLE ::        A(:,:), X(:), T(:)
      REAL, ALLOCATABLE ::        A0(:,:), T0(:), QR0(:,:), QRAUX0(:)

      REAL, (KIND(1E0))SDOT

      PARAMETER      (NRA=4, NCA=3, LDA=NRA, LDQR=NRA)

!                                 Set up for MPI

      MP_NPROCS = MP_SETUP()
      IF(MP_RANK .EQ. 0) THEN
          ALLOCATE (A(LDA,NCA), X(NCA), T(NCA), IPVT(NCA))

!                                 Set values for A and the righthand side

          A(1,:) = (/ 1.0,  2.0,   4.0/)
          A(2,:) = (/ 1.0,  4.0,  16.0/)
          A(3,:) = (/ 1.0,  6.0,  36.0/)
          A(4,:) = (/ 1.0,  8.0,  64.0/)
!
          X      = (/ 1.0,  2.0,   3.0/)

!

          IPVT = 0
      ENDIF

!                                  Set up a 1D processor grid and define

!                                  its context ID, MP_ICTXT

      CALL SCALAPACK_SETUP(NRA, NCA, .TRUE., .TRUE.)

!                                  Get the array descriptor entities MXLDA,

!                                  MXCOL, MXLDB, MXCOLB

      CALL SCALAPACK_GETDIM(NRA, NCA, MP_MB, MP_NB, MXLDA, MXCOL)

      CALL SCALAPACK_GETDIM(NCA, 1, MP_NB, 1, MXLDB, MXCOLB)

!                                  Set up the array descriptors

      CALL DESCINIT(DESCA, NRA, NCA, MP_MB, MP_NB, 0, 0, MP_ICTXT, MXLDA, &
      INFO)

      CALL DESCINIT(DESCL, 1, NCA, 1, MP_NB, 0, 0, MP_ICTXT, 1, INFO)

      CALL DESCINIT(DESCB, NCA, 1, MP_NB, 1, 0, 0, MP_ICTXT, MXLDB, &
      INFO)

!                                   Allocate space for the local arrays

      ALLOCATE (A0(MXLDA,MXCOL), QR0(MXLDA,MXCOL), QRAUX0(MXCOL), &
                IPVT0(MXCOL), T0(MXLDB))

!                                 Map input array to the processor grid

      CALL SCALAPACK_MAP(A, DESCA, A0)
      PIVOT = .TRUE.

 

      CALL SCALAPACK_MAP(IPVT, DESCL, IPVT0)

!                                 QR factorization

      CALL LQRRR (A0, QR0, QRAUX0, PIVOT=PIVOT, IPVT=IPVT0)

!                                 Unmap the results from the distributed

!                                 array back to a non-distributed array.

!                                 After the unmap, only Rank=0 has the full

!                                 array.

      CALL SCALAPACK_UNMAP(IPVT0, DESCL, IPVT, NCA, .FALSE.)

      IF(MP_RANK .EQ. 0) CALL PERMU (X, IPVT, T, IPATH=1)

      CALL SCALAPACK_MAP(T, DESCB, T0)

      CALL LSLRT (QR0, T0, T0, IPATH=4)

      CALL SCALAPACK_UNMAP(T0, DESCB, T)

!                                Print results.

!                                Only Rank=0 has the solution.

      IF(MP_RANK .EQ. 0)THEN

         Q = SDOT(NCA, T, 1, T, 1)

         CALL UMACH (2, NOUT)

         WRITE (NOUT, *) ‘Q = ‘, Q

      ENDIF

!                                Exit ScaLAPACK usage

      CALL SCALAPACK_EXIT(MP_ICTXT)

!                                Shut down MPI

      MP_NPROCS = MP_SETUP(‘FINAL')
      END

Output

 

Q =    0.840624

Visual Numerics, Inc. Visual Numerics - Developers of IMSL and PV-WAVE http://www.vni.com/ PHONE: 713.784.3131 FAX:713.781.9260