Univariate Quadrature
The first nine routines described in this chapter are designed to compute approximations to integrals of the form
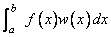
The weight function w is used to incorporate known singularities (either algebraic or logarithmic), to incorporate oscillations, or to indicate that a Cauchy principal value is desired. For general purpose integration, we recommend the use of QDAGS (even if no endpoint singularities are present). If more efficiency is desired, then the use of QDAG (or QDAG*) should be considered. These routines are organized as follows:
• w = 1
− QDAGS
− QDAG
− QDAGP
− QDAGI
− QDNG
• w(x) = sin ωx or w(x) = cos ωx
− QDAWO (for a finite interval)
− QDAWF (for an infinite interval)
• w(x) = (x − a)α (b − x)β ln(x − a) ln(b −x), where the ln factors are optional
− QDAWS
• w(x) = 1/(x −c) Cauchy principal value
− QDAWC
The calling sequences for these routines are very similar. The function to be integrated is always F; the lower and upper limits are, respectively, A and B. The requested absolute error ɛ is ERRABS, while the requested relative error ρ is ERRREL. These quadrature routines return two numbers of interest, namely, RESULT and ERREST, which are the approximate integral R and the error estimate E, respectively. These numbers are related as follows:
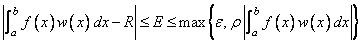
One situation that occasionally arises in univariate quadrature concerns the approximation of integrals when only tabular data are given. The routines described above do not directly address this question. However, the standard method for handling this problem is first to interpolate the data and then to integrate the interpolant. This can be accomplished by using the IMSL spline interpolation routines described in Chapter 3, “Interpolation and Apprximation”, with one of the integration routines CSINT, BSINT, or PPITG.
Multivariate Quadrature
Two routines are described in this chapter that are of use in approximating certain multivariate integrals. In particular, the routine TWODQ returns an approximation to an iterated two-dimensional integral of the form
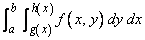
The second routine, QAND, returns an approximation to the integral of a function of n variables over a hyper-rectangle
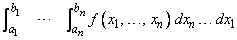
If one has two- or three-dimensional tensor-product tabular data, use the IMSL spline interpolation routines BS2IN or BS3IN, followed by the IMSL spline integration routines BS2IG and BS3IG that are described in Chapter 3, Interpolation and Approximation.
Gauss rules and three-term recurrences
The routines described in this section deal with the constellation of problems encountered in Gauss quadrature. These problems arise when quadrature formulas, which integrate polynomials of the highest degree possible, are computed. Once a member of a family of seven weight functions is specified, the routine GQRUL produces the points {xi} and weights {wi} for i = 1, …, N that satisfy
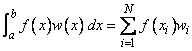
for all functions f that are polynomials of degree less than 2N. The weight functions w may be selected from the following table:

Where permissible, GQRUL will also compute Gauss-Radau and Gauss-Lobatto quadrature rules. The routine RECCF produces the three-term recurrence relation for the monic orthogonal polynomials with respect to the above weight functions.
Another routine, GQRCF, produces the Gauss, Gauss-Radau, or Gauss-Lobatto quadrature rule from the three-term recurrence relation. This means Gauss rules for general weight functions may be obtained if the three-term recursion for the orthogonal polynomials is known. The routine RECQR is an inverse to GQRCF in the sense that it produces the recurrence coefficients given the Gauss quadrature formula.
The last routine described in this section, FQRUL, generates the Fejér quadrature rules for the following family of weights:

Numerical differentiation
We provide one routine, DERIV, for numerical differentiation. This routine provides an estimate for the first, second, or third derivative of a user-supplied function.
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |